-
Notifications
You must be signed in to change notification settings - Fork 25
ProgressReport05232010
Table of Contents:
Integrating the flow invariants worked out well. We found the desired Daikon invariant that accompanies the transition ack -> send: send.fragment - ack.fragment = 1. An obvious issue with the resulting representation below is that the invariant list must be made more concise to be readable:

If we make role and fragment to be non-comparable, the following representation emerges. This representation raises the question of whether there are generic non-comparability assumptions that work well. For example it might be in general a good idea to not consider the sender's address (e.g. role here) to be comparable with other message fields.

We realized that the final representations derived with splitting could be made much more compact if certain nodes were merged (see the last progress report, for an example where this is true). We believe that that reason behind why the final representation is not as compact as it could be is that we do not have a good enough heuristic to choose the split partition when no split of any partition can resolve an invalid temporal invariant.
As a result, we implemented a merge phase (i.e. GK-tail with K=1?) following the split phase. In particular, we perform a merge only if the resulting representation retains all the temporal invariants. For the Peterson representation from last week, we get the following:
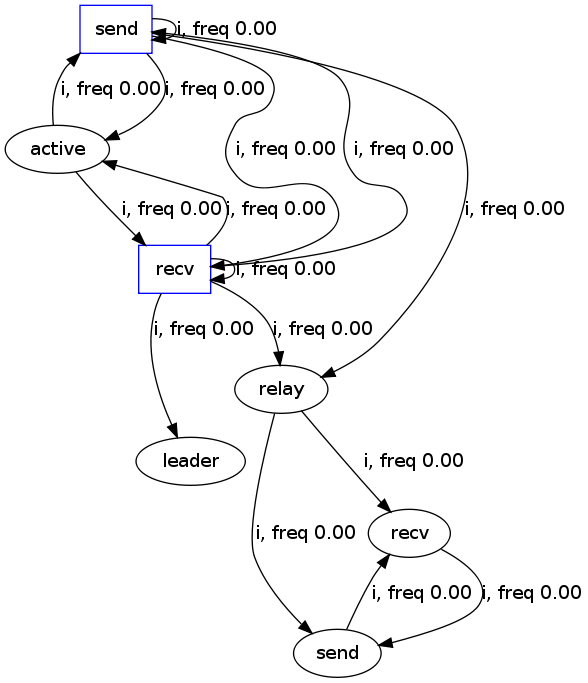
The above representation is promising because we do not think it can be made more compact. A particular feature of this graph are a few strongly connected components that just beg for further simplification (we come back to this later in the report).
This simple hybrid algorithm (mixing splitting and merging), however, raises a question regarding how we may characterize the resulting representation. In particular, is it possible to derive the representation derived with the above hybrid algorithm using only splits?
Turns out, the answer is that it is not always possible.
In summary, the reason for this is that the decision to perform a split is made only according to the presence or absence of a transition. If there is no distinguishing transition feature in the original trace, the split may be impossible.
Specifically, consider the following diagram, and the corresponding reasoning:

The initial partition ABCD (containing messages from the trace -- A,B,C,D of same type) cannot be split by any combination of splits into partitions AC and BD, because we may not have a distinguishing transition that all messages in AC take, but all nodes in BD do not take, or vice versa. However, it may be the case that we may split ABCD into AD and BC because, for example, there is a transition X that AD takes and BC does not take. Similarly, there may exist transitions Y and Z that separate AD into A and D, and BC into B and C respectively. However, in sum the transitions X, Y, and Z do not imply the existence of a transition that separates AC and BD. Now that we have A, B, C, and D separated out, the merge algorithm may merge A with C, and B with D without violating any invariants (note: this may require a GK-Tail parameter k > 1).
The reasoning above is informal. We hope to write-up a concrete counter-example.
If the above is to be believed, it has significant implications for the space of representations we are considering. In particular, this implies that merges and splits are not necessarily inverses of one another. So instead of a single dimension of representations, where split and merge act as refining\coarsening operations, we have a more complex space. Because splits cannot reproduce the affect of certain merges, perhaps they are better thought of as orthogonal operations. This yields the following picture concerning the reachability of representations with merge\split operations:
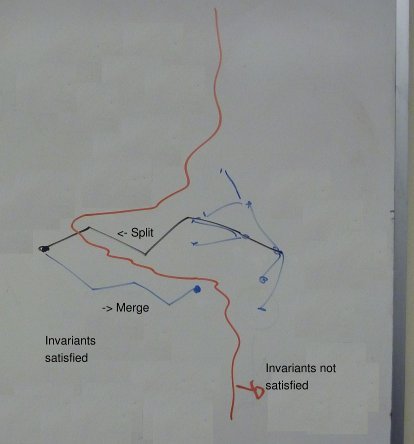
The black line indicates a series of splits made until the invariants are satisfied. It might be the case that the final representation can be compacted by merging without invalidating any invariants. The final result of merging may not be reachable by splitting, and it may be more compact than the representation derived with splitting alone.
The reason for considering such a hybrid algorithm in the first place was that it produced a more compact representation. We believe that this might be true of such hybrid algorithms in general.
In the Peterson representation above, the strongly connected components (SCCs) are not very helpful to the reader. Intuitively such components indicate that everything can happen, which signals concurrency in the system.
To improve the representation we decided to replace an SCC in the representation with a box indicating the dependency constraints (i.e. inferred invariants) on the messages mined from the sub-trace associated with the SCC.
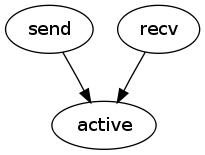
From the SCC in the above graph among messages [active, send, recv] we mine the following dependencies. We mined that active depends on the sends and recvs preceding active, but that there are no dependencies between send and recv. (See below for a more detailed discussion.)
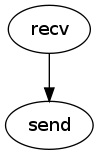
For the SCC among [send, recv] that follows relay we get the following dependencies. Note that these are exactly what we want! Also note that the output could be enhanced by using Daikon to infer that the payload is forwarded (i.e. unchanged between recv and send).
Ideally, for the SCC [active, send, recv] we would get the invariant recv[mtype=1] AP send[mtype=2]. As it turns out, the most closely related structural invariants we mine is
recv[id <= 20, localRoundId <= 18, mtype >= roundId, roundId one of { 0, 1 }, roundId <= 1, roundId is boolean, roundId == roundId**2, roundId == roundId**2]
AP send[id >= 2, id > mtype]
First we thought this is an artifact caused by the fact that we only used the traces of 15 different runs of a 5 node system. But for 150 different runs of a 5 node system, we get the following (very similar) set of invariants, which is not much better.
recv[id <= 20, roundId one of { 0, 1 }, roundId <= 1, roundId is boolean, mtype >= roundId, roundId == roundId**2, roundId == roundId**2]
AP send[id >= 2]
The problem seem to be that in many of the traces recv[mtype=2] precedes send[mtype=2] as well. Our mining algorithm constructs two sets of messages: The set A of recv-messages that appear before send-messages in the trace, and the set B of send-messages that appear after recv-messages in the trace. We then use Daikon to infer invariants over A and B, which yields the invariants above.
It might be useful to specialize the generated invariants and test whether the specialized invariants hold. This is the Daikon approach applied to temporal invariants. As an example of this, from the invariant above, we test the specialized invariant by taking a value from the "one of" clause. Which produces invariants that are not exactly what we want, but closer to the intended goal:
recv[id <= 20, roundId==1, mtype >= roundId]
AP send[id >= 2]
One reason for the over-splitting mentioned in the last progress report, and which caused us to consider the hybrid split-merge algorithm above, is the heuristic to select the partition to split.
For some graphs, no single split will eliminate an invariant violation. This means that the algorithm must guess a number of splits until measurable progress is made.
Our current heuristic is to choose the second to last partition in a violating trace if no possible choice of partition eliminates a violation.
We are currently investigating another heuristic to pick a partition. The heuristic is described in ["Counterexample-Guided Abstraction Refinement", by Edmund Clarke, Orna Grumberg, Somesh Jha, Yuan Lu, and Helmut Veith. CAV 2000].