ProgressReport05182010
Table of Contents:
Last week we discussed the graphical user interface. We collected a proposal of features that the Synoptic GUI should have into the SynopticGUI page.
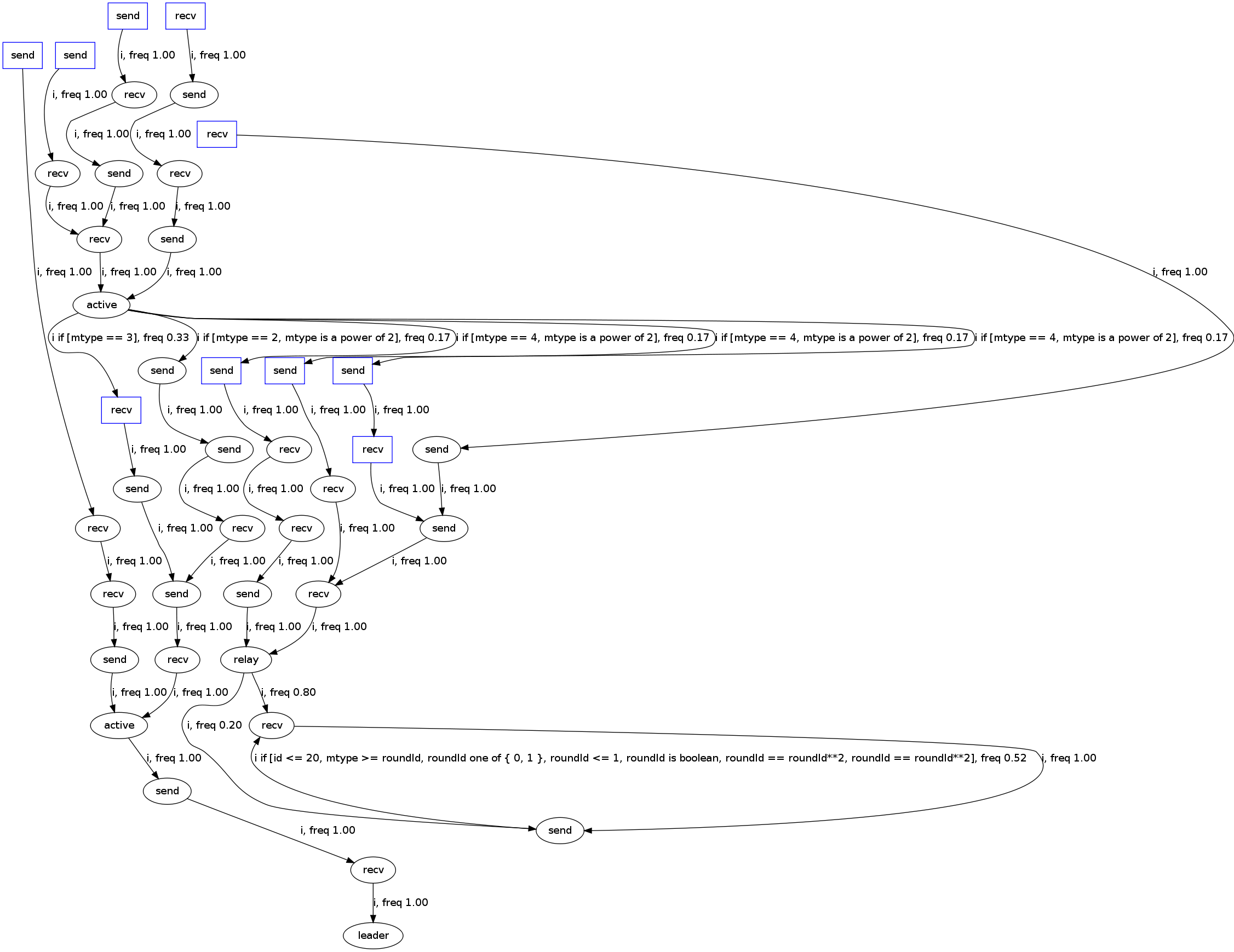
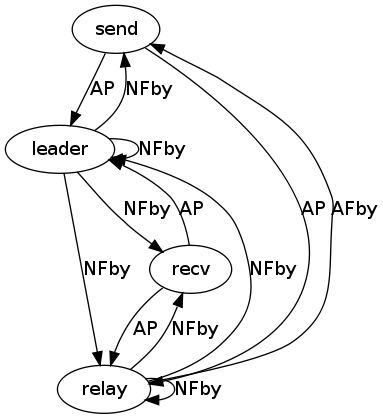
Because the Peterson algorithm is quiet complex we decided to experiment with a different, simpler protocol. We implemented the Stenning data link protocol, which provides a reliable FIFO communication channel between two parties in an unreliable network that may reorder packets. A description of this protocol is available here.
Running synoptic on the output trace of this protocol, we get the following representation:
While the generic structure of the protocol is captured, we fail to present the resend-on-loss mechanics, i.e. the fragment carried by send and the fragment acknowledged by ack are not exposed in the graph.
Consider the following interaction trace between nodes 0 and 1. They alternate sending messages to one another as follows:
NodeId Payload
0 0 send
1 0 ack
0 1 send
1 0 ack *
0 1 send
1 0 ack *
0 1 send
1 1 ack +
The marked (*) acks acknowledge the last received fragment 0, not the last fragment sent by node 0, which is fragment 1. In the protocol this is the behaviour to indicate that the current fragment (here fragment 1) must be resent. Only after fragment 1 is finally received and acknowledged (+), the protocol can proceed with fragment 2. This whole mechanic is not exposed in our graph. This is because we would have to split a partition based on the observation that the payload of the next send only increases if ack.Payload matches send.Payload (of the previously sent send-message).
Looking at the Peterson representations, we realized that the splitting heuristic (of splitting the first invalid node in a counter-example trace) does not work as well as we anticipated. In the representation the algorithm splits out several portions of the graph even though this is not necessary for invariant satisfaction. We therefore investigated whether the partition selection technique from ["Counterexample-Guided Abstraction Refinement", by Edmund Clarke, Orna Grumberg, Somesh Jha, Yuan Lu, and Helmut Veith. CAV 2000] can be applied in our setting.
As example, consider the second and third send node on the top of the graph counted from the left. There is no invariant that could force those to to be separate partitions, yet the trace is split at that point. During the development of the algorithm, it became apparent that sometimes no single split can satisfy an invariant, but rather a sequence of splits. In such cases, it is difficult to pick the right split to begin with. The conjecture is that we do not pick the right splits and end up splitting much more than is necessary. More such examples can be found allover the graph, e.g. the send nodes (and their successors) in the middle part of the graph.
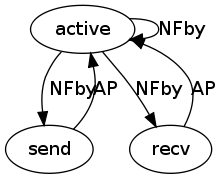
We partitioned the Peterson trace by local node's round id and studied the "invariant fingerprint" independent rounds to see if they could be groups\classified. We found several characteristic invariants schemata:
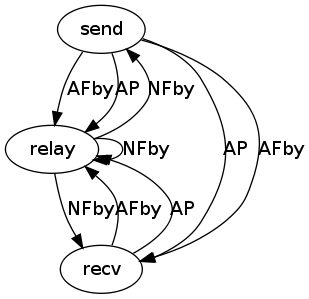
We noticed that the schemata are not always exactly the same; small variations exist:
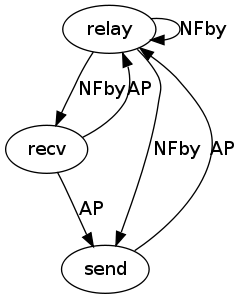
We have not implemented an automatic classification yet.
We found Jung, a Java Graph Library, which we will use to display our graphs. The library seems to provides all features we need. We will bring a first demo to our weekly meeting.