-
Notifications
You must be signed in to change notification settings - Fork 25
ProgressReport04132010
Table of Contents:
- Implement common graph structure for gkTail and Bisim, i.e. one is used for storage, the other is generated on the fly (see below for problems)
- Integrated full fledged did/can LTL model checker (which we do not use)
- Implemented some caching for the LTL model checker
-
Extended the graph to handle multiple relations. The idea is to overlay multiple relations onto the same representation to present multiple perspectives to the user. We applied this to present a global system perspective (temporal relation between all msgs) and a node's perspective (temporal relation between all msgs from a node).
-
Applied the multiple relations view to a manually generated trace of the Peterson's election algorithm for uni-directional asynchronous networks. More information about this algorithm is here.
-
Implemented merge/split for partitions, and merge for states. All three split/merge operations in the graph are reflected in both graph representations.
It turns out that neither of the graph representations can represent all information of the other, i.e. there is no bijection between the graph representations (although we assumed this last quarter). For example, the number of initial/terminal states in the system-state based representation cannot be reflected in the bisim representation:
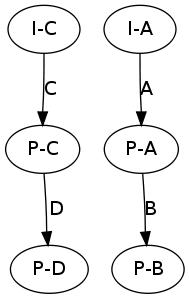
Merging the initial states above yields:
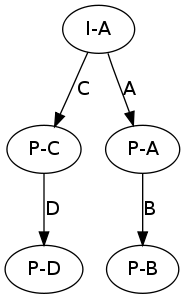
This operation does not impact the equivalent bisim representation (it is the same for both graphs above) because in the bisim representation there is no notion of a system state. In gkTail, all traces from the same node are assumed to begin from the same initial system state. While different nodes are assumed to begin in different start states. In bisim, no explicit assumption about system state is made.
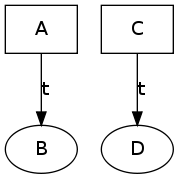
If non-initial states are merged, we could introduce new edges into the bisim graph. The semantic intuition behind this is that if gkTail decides to merge two states it is probable that they represent the same system state. But this in turn means, that they should be able to produce the same messages. For example, starting from the first graph above and merging the state P-C in the middle level into P-A could yield the following graphs:
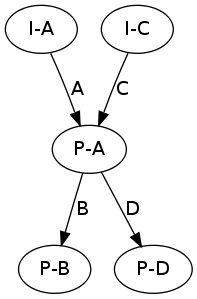
Observe that two new edges have been added to reflect that from P-A both messages B and D are possible.
The graph structure was extended to allow several relations between message partitions. The input graph now is annotated with the relation "i" to capture the timely order of events at a node, i.e. messages are "i" related if there is a node at which they happened immediately after one another.
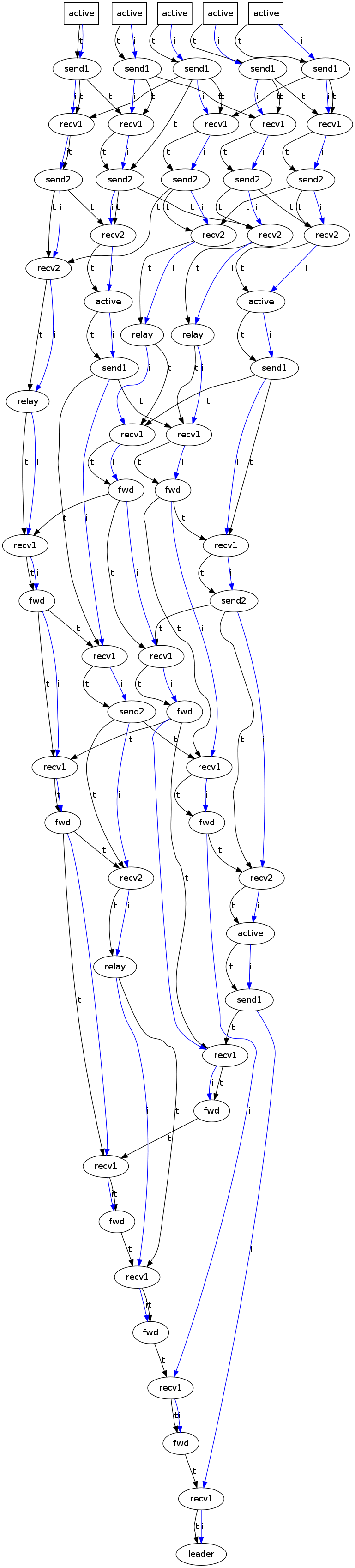
Note that the results for minimizing with respect to "t" (globally immediately after one another relation) contains a "spurious" path that violates the assumed invariant relay neverFollowedBy active:
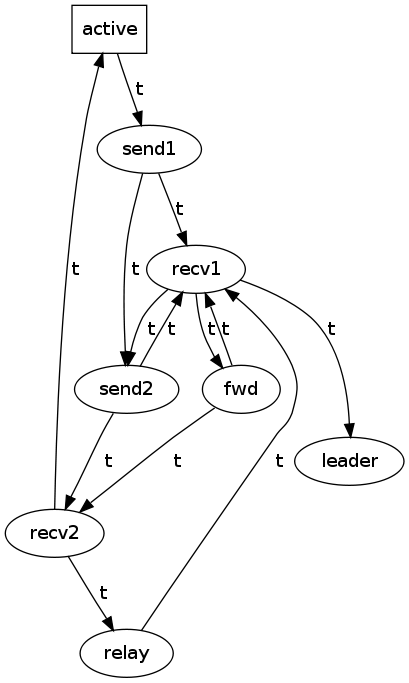
Since we are capturing the timely relation of the global system, this invariant does not hold - after node A enters relay state, node B can legally enter active state.
Minimizing the trace with respect to node-local events (i.e. relation "i"), yields the following graph, which precisely and correctly describes node behaviour:
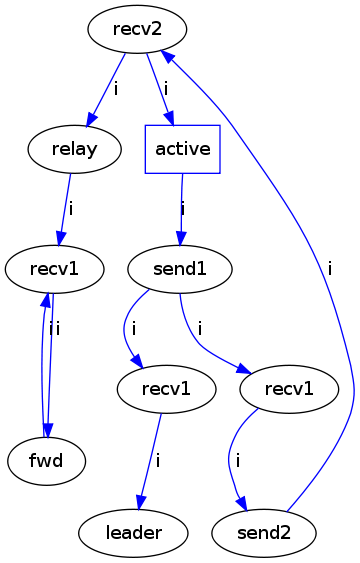
The results for the combined graphs is below. To 'combine' the two graphs, the two relations were treated simultaneously. That is, the invariants for the two relations were combined into a set and the algorithm proceeds as before -- at each step the algorithm resolves one invariant from this set with the shortest counter-example path until all invariants are satisfied.
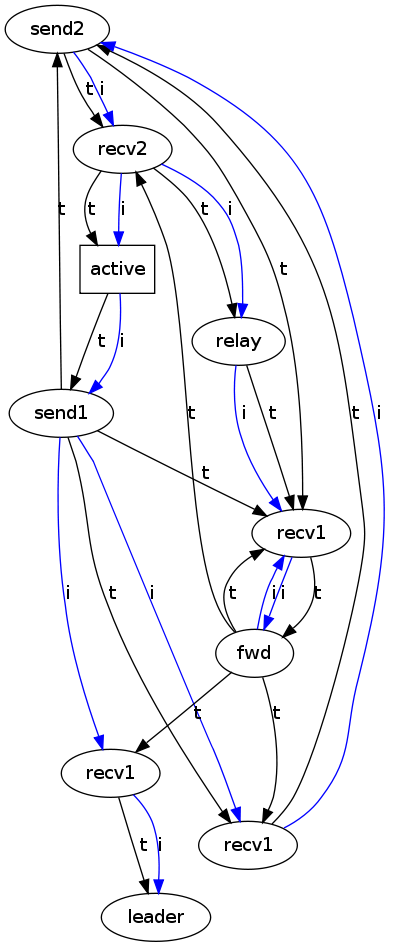
This indicates that on the one hand combining the relations and treating invariants over different relations together works. On the other hand, the graph is basically the i-graph from above with temporal relations added in - and in fact, the two crucial invariants to get the graph right are fwd neverFollowedBy(i) leader and fwd neverFollowedBy(i) send2, i.e. including the relation t bought us nothing. This raises the question of how we may identify useful global properties -- those that contribute to system summarization.
The goal of an algorithm competing in the StaMinA competition is as follows: given a list of strings that satisfy (positive examples) and do not satisfy (negative examples) some hidden FSM, produce this FSM or a similar FSM solely based on the input behavior. The output FSM is tested against a different set of data (not the input) for a score. This competition lasts until December, so we have plenty of time to participate.
There are few ways in which we may minimally adapt Bikon to see how it performs in this competition:
- Add a new symbol to the FSM alphabet -- Accept.
- Modify input strings such that positive strings terminate with Accept symbol.
- Consider only the positive strings as input to Bikon, and run the algorithm until it terminates.
- Add an implicit invariant that negative examples are NeverFollowed by an Accept symbol.
- Consider the negative strings as counter-examples to some possibly
hiddeninvariant that we may not surmise. If a negative string is not satisfied by the graph from the previous step then we find the first non-satisfying node and split it (as before). We do so under the constraint that after each such split the resulting graph must continue to satisfy the positive strings.
The changes above merely adapt Bikon. It would be interesting to see how this version of the algorithm would perform in the competition. An example of a more in-depth change to Bikon would be to augment the set of Bikon invariants to reason about negative strings. Also note that the symbols\messages in this competition do not have any structural data. So adding Daikon should not make a difference since no structural invariants can be derived. These ideas and more have been factored out into the StaMinACompetition2010 wiki page.
- Finalize translation
- Get gkTail working again
- Start with Daikon integration