-
Notifications
You must be signed in to change notification settings - Fork 24
ProgressReport04202010
Table of Contents:
Peterson's election algorithm is highly concurrent and can function in asynchronous networks. Because of this, it represents a perfect test case for Synoptic. We built a simulator to generate valid traces for arbitrary number of nodes in the ring network, and also added a seed parameter to control non-determinism in the system. The seed controls for things like:
-
The assignment of initial ids to nodes
-
The order in which nodes execute their operations in any single round (e.g. node 3 then node 2, ..)
-
The order of operations on a single node: sending first id, sending second id, or changing state
The simulator does not overlap rounds -- all nodes must finish a round before the simulator proceeds to the next round. The complexity of the resulting traces seems to sufficiently stress our representation (see below), so implementing overlapping rounds would probably be overkill.
Note that there are a few changes to the output format of the simulator from the previous traces: the relay node no longer sends/generates fwd messages but instead generates send1 or send2 messages. It generates a send1/send2 message if the node sending it the message sent the message as a send1/send2. In a sense, the relay is supposed to function transparently to the receiver, therefore it replicates whatever the sender did exactly.
We've found that both split and merge have interesting invariant preservation properties. These properties are helpful in 'mapping out' the space of representations with respect to invariant satisfaction 'axes.'
Remember that we have four types of temporal invariants: NeverFollows (NF), AlwaysFollows (AF), NeverPrecedes (NP), and AlwaysPrecedes (AP). These invariants are satisfies by all the observed traces.
For the split operation we observe the following:
- AF and AP are always satisfied in the initial partitioning
- Splitting will never violate an invariant that was already satisfied. This is true for all 4 invariant types above.
The NF and NP can be introduced in the initial partitioning because messages are merged. Its interesting to note that the second observation is a form of a progress invariant for split, and implies that if visualized invariants are indeed half open intervals -- once achieved, they can never be falsified.
For the merge operation we observe the following:
- All invariants are satisfied in the initial graph
- Merging can only violate NF and NP, but never AF or AP.
Initially, the GK graph captures the trace exactly. Because invariants are mined from the trace, the graph must adhere to the invariants. AF and AP are never falsified because merging cannot eliminate paths between message types that always co-appear.
We investigated the concurrency resilience of the algorithms. For this purpose the Peterson trace generator was modified to exhibit maximal concurrency (see above).
In the following graph each connected component represents a possible interleaving of the several independent processes running at each node:
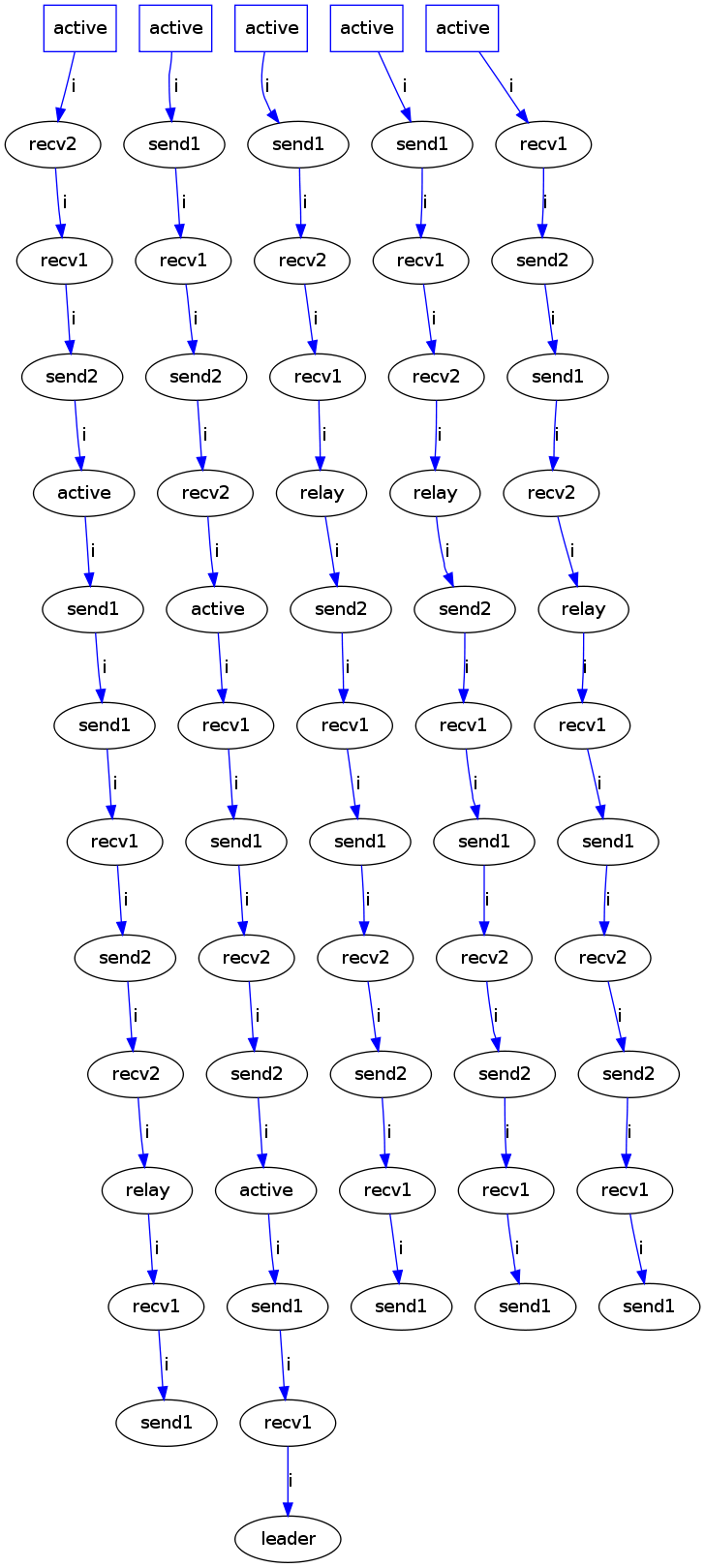
Bisim compresses the above graph as follows:
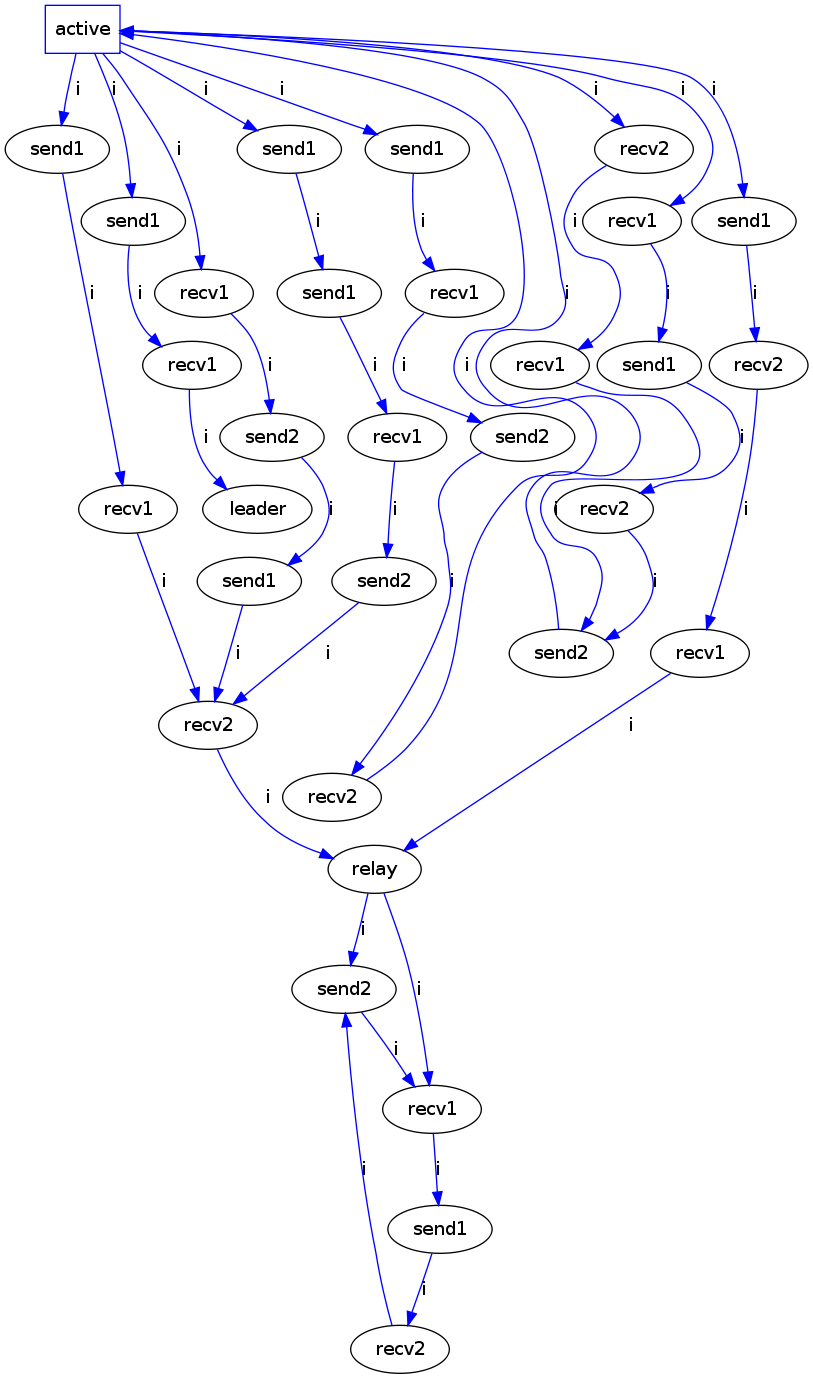
Notice that bisim fails to recover the underlying processes from the observed interleavings.
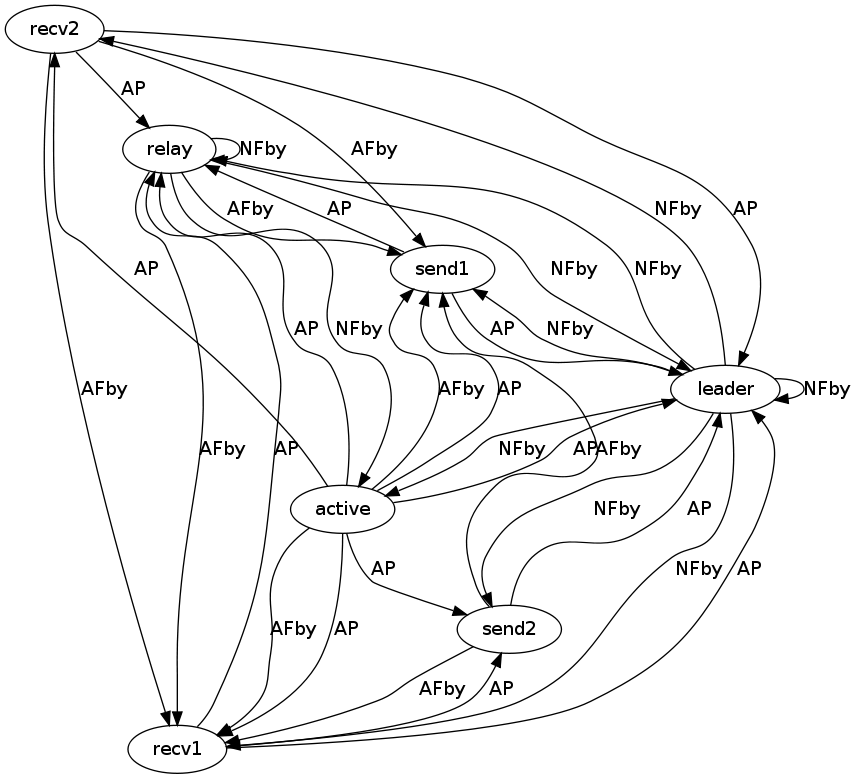
We also noticed that important ordering relations were recovered from our invariant mining step. In this graph, we show the invariant relationships we mined between the different messages. These include AP (always precedes), AFby (always followed by), and NFby (never followed by):
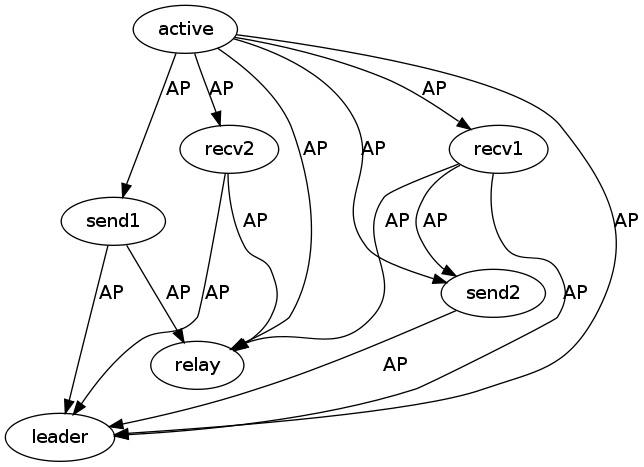
Here is an AP (always precedes) invariant sub-graph of the above. The
invariant AP shows that recv1 AlwaysPrecedes send2 is the important
ordering.
For us, the ground truth at the nodes seems to be the following decomposition into concurrent processes.
| Process1 | Process2 | Process3 |
|---|---|---|
| recv1 | send1 | recv2 |
| send2 |
We know that all interleavings must be legal in the observed system if
we have no other invariants than recv1 AlwaysPrecedes send2, because
then we have a trace constituting a counter-example for all other
possible invariants. Note that additional traces cannot lead to new
invariants. However, with fewer traces we might infer invariants that
are not present in the system.
We want to represent the table above concisely as a graph network. We discovered that petri nets are a natural representation for concurrency. Here is an example petri net for the pattern above. In particular, recv1 and send2 are serial linked because there is an invariant forcing them into this configuration. However, the other two messages -- send1 and recv2 can execute concurrently. The petri net also shows that all three paths must execute before the system can continue to the next state. Below the squares are petri net transitions, and the circles are petri nets places. The initial marking for our execution traces is one in which P0 contains three tokens. Note that the "init" and "end" transitions had to be artificially added -- they do not exist in the traces.
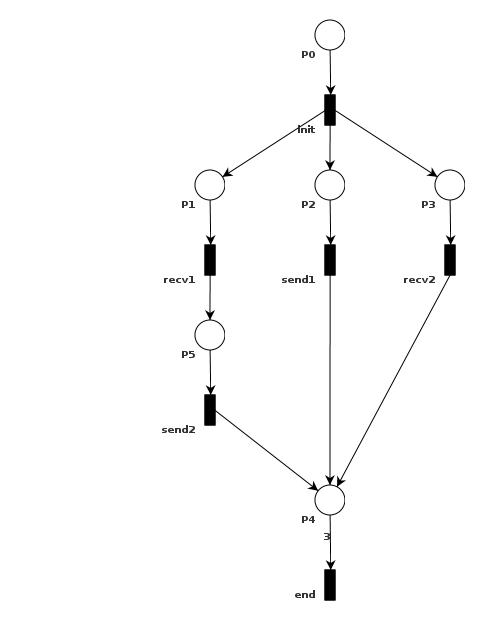
We have begun to explore how we can adapt our algorithms to work on petri nets. We believe that petri nets have a few advantages and disadvantages over our current preferred representation:
-
Petri nets naturally capture concurrency, which is necessary to capture distributed systems execution accurately
-
Petri nets are strictly more powerful, so any bisim or GK graph can be represented as a petri net
-
Petri nets have a notion of state (a marking) that corresponds to the intuition behind using the GK representation -- that the system is a state machine of some sort. They also have a rich notion of transition which corresponds to the bisim representation of elevating messages first class citizens. It therefore provides the flexibility and expressiveness of both worlds.
-
Its unclear how multiple relations (an advantage of bisim representation) can be represented in petri nets. Surely, multiple colored petri nets may be overlayed on top of the same transitions (squares above) and places (circles above). However, the resulting diagram would be much more difficult to read. Although perhaps, multiple relations are not easy to read in the bisim representation either.
In the following, the incremental steps of building the net. The last net is dysfunctional, the image is included for discussion purpose.
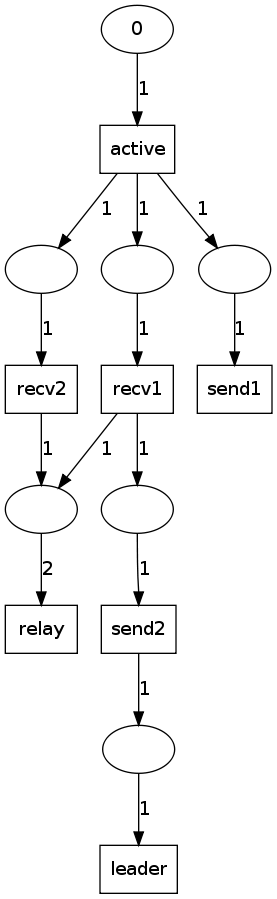
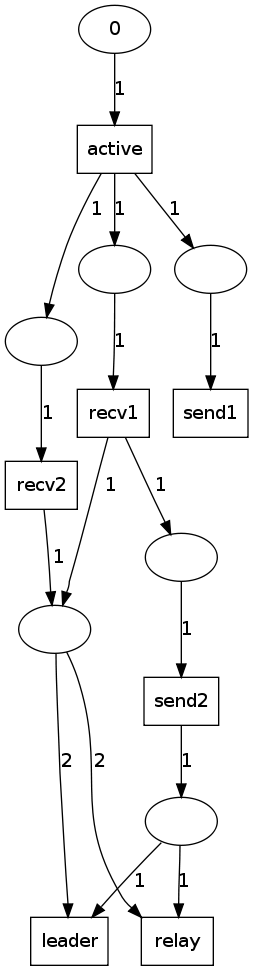
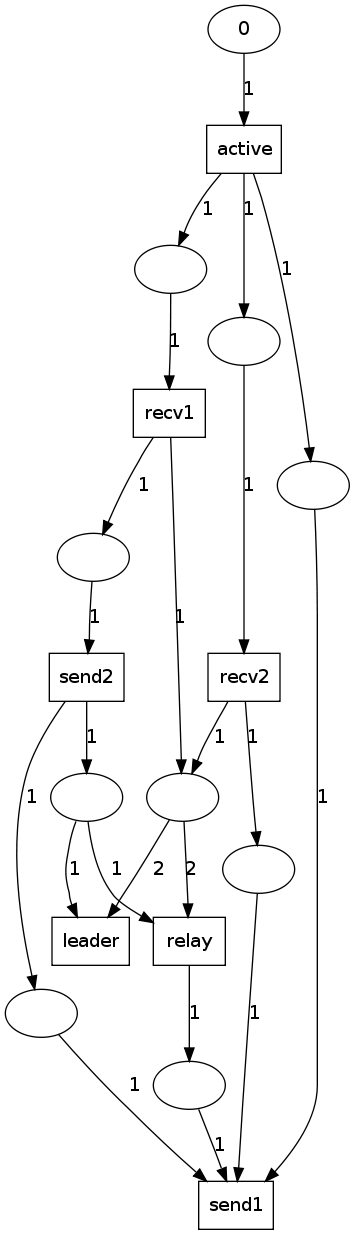
-
Begin Daikon integration ?
-
Consider how to capture concurrency with partial use of petri nets or convert the entire pipeline to use the petri net representation ?