Turing Patterns: A C++/CUDA application for simulating 2D reaction-diffusion dynamics showing diffusion driven instability
This repository implements the numerical schemes for simulating the most popular reaction diffusion dynamics that exhibits Turing instability.
The general two-dimensional PDE is of the form:
The numerical scheme implemented is a simple Forward Euler scheme, which is known to be unstable but easy to implement. As opposed to the usual stability condition, the introduciton of a source term makes it more unstable, although dt in the region of dx^2 seem to be a reasonable choice. An extension to this could be a Runge-Kutta solver or an IMEX scheme, where the source term is considered in the explicit portion.
The Finite Difference schemes are implemented in CUDA. Since the non-linear nature of the dynamics I found it easier to implement without making use of CuBLAS.
The dynamics that I've implemented are:
- Gray-Scott
- Brussellator
- Schnakernberg
- Thomas
- Fitz-Hugh Nagumo
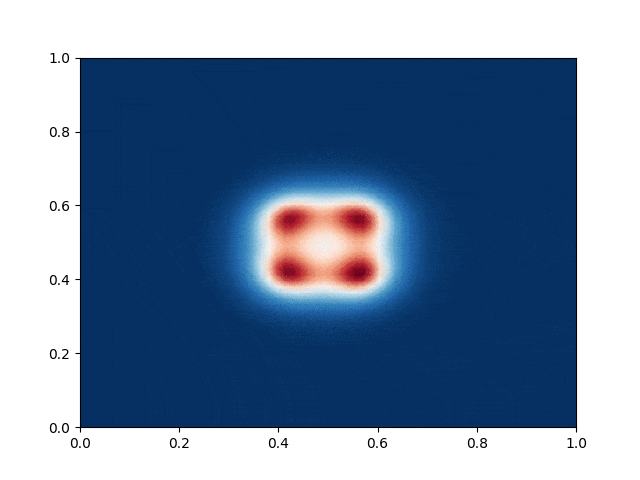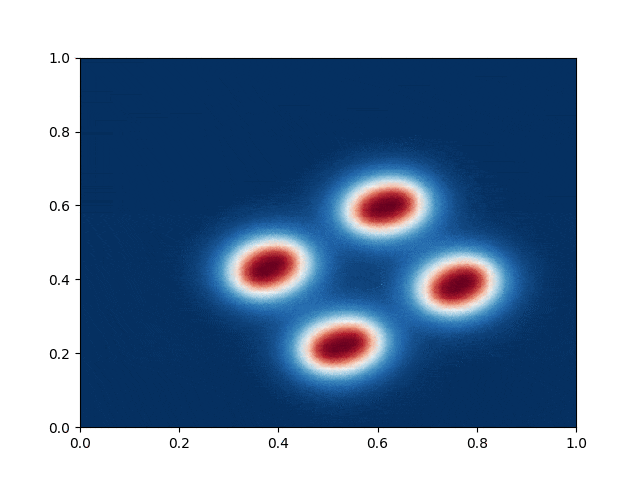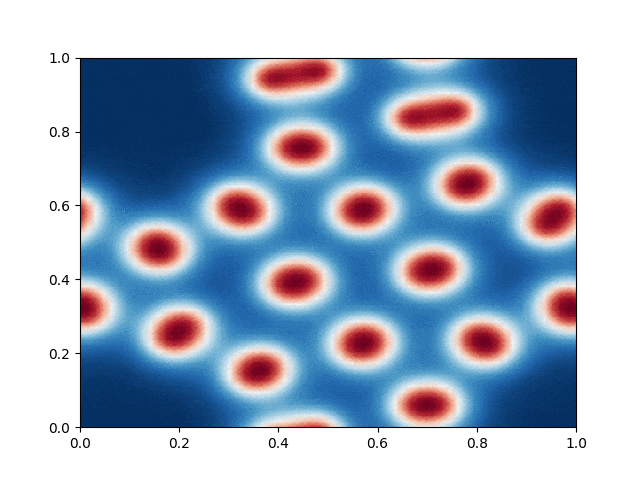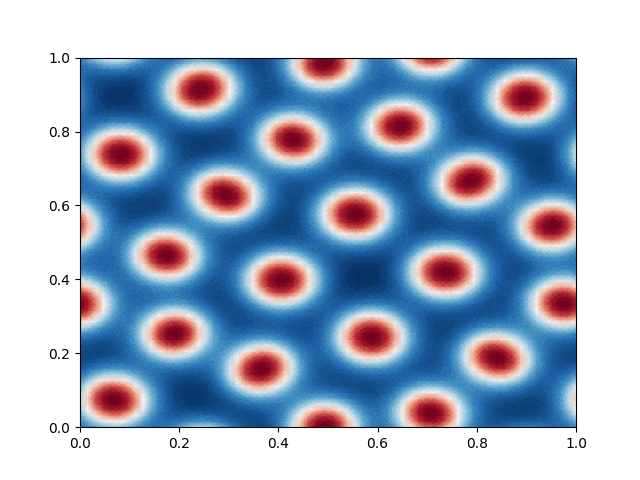
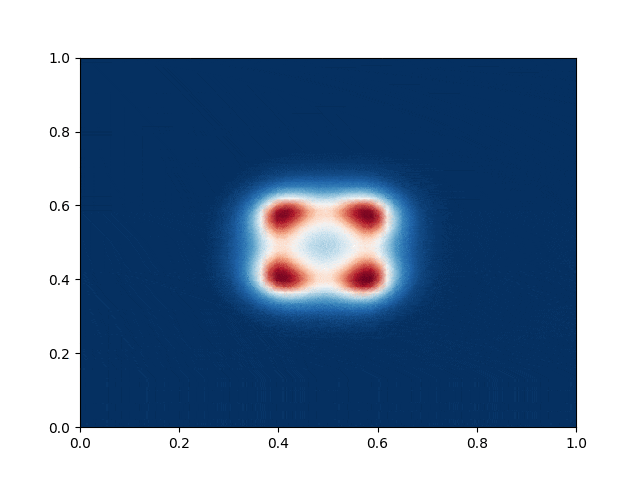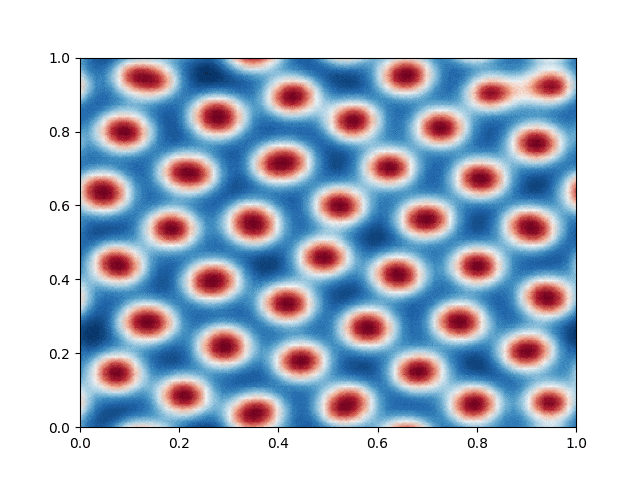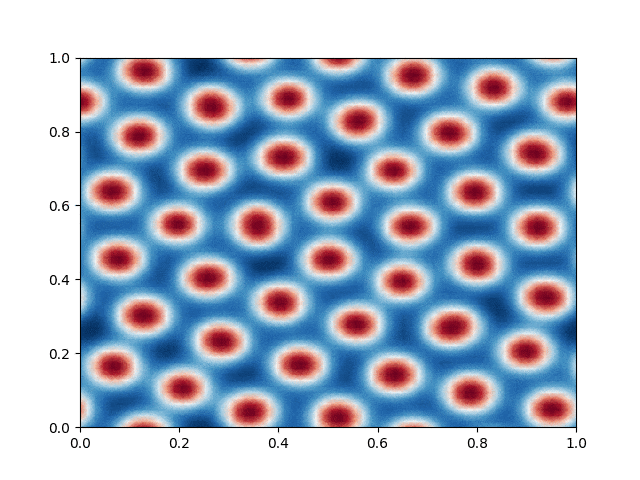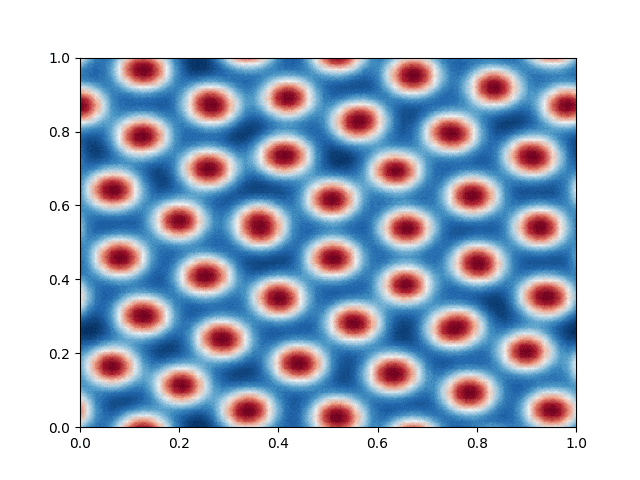
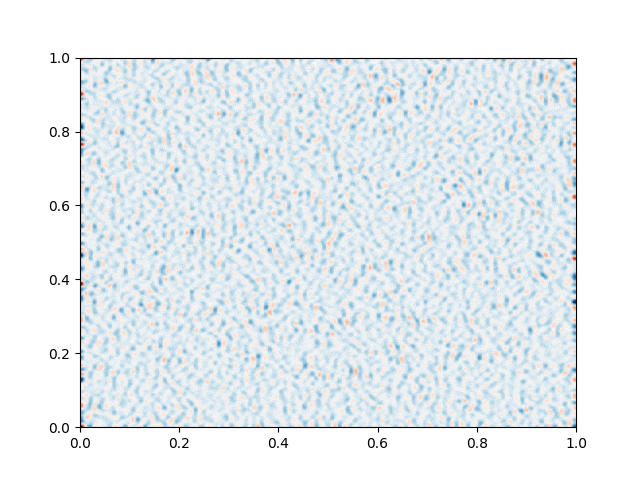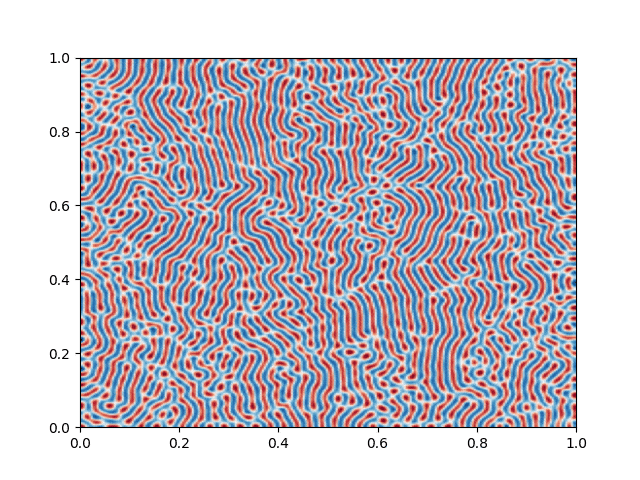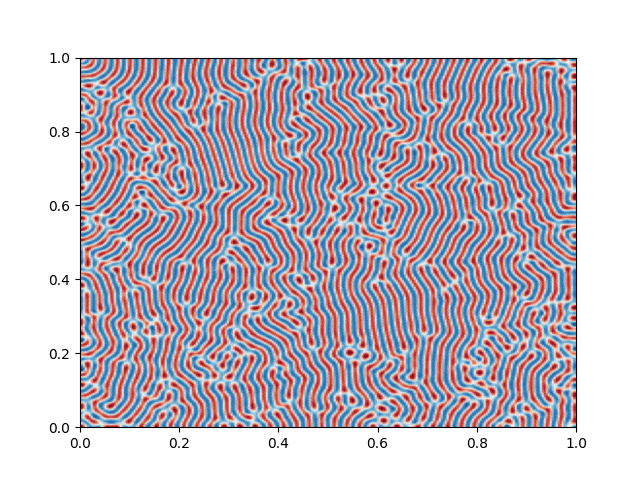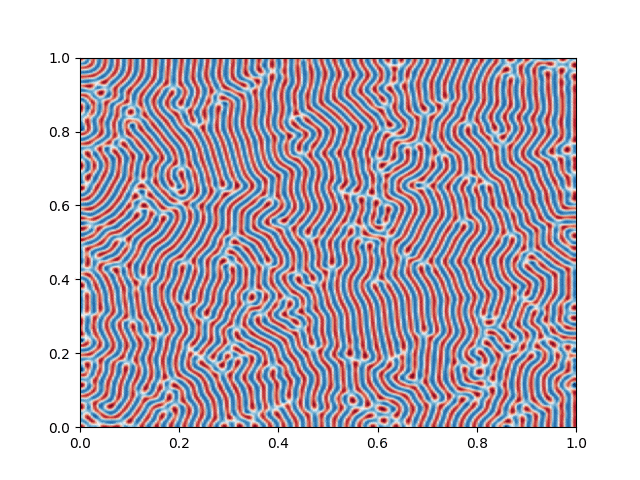
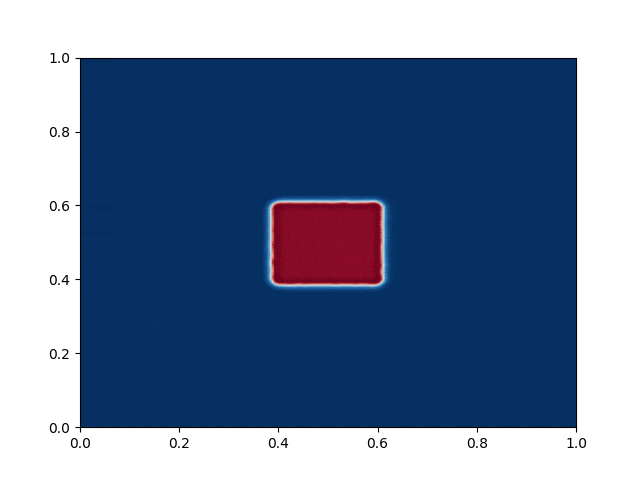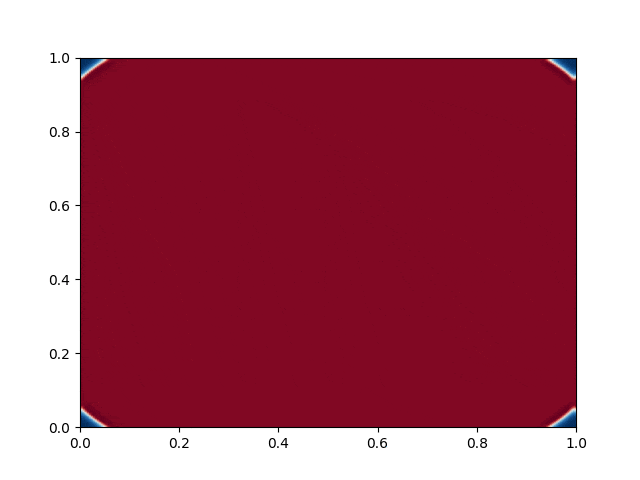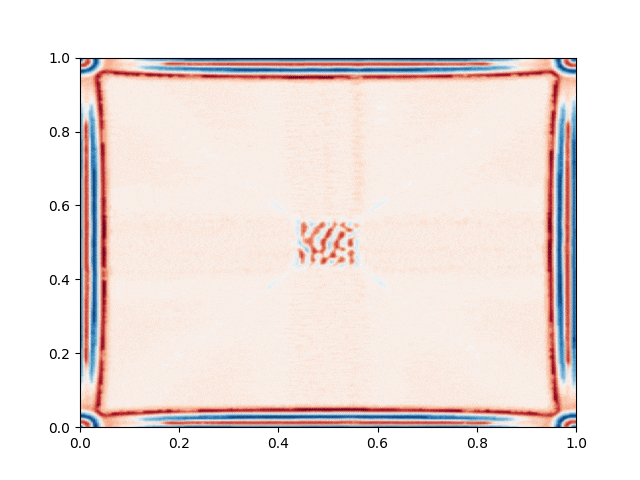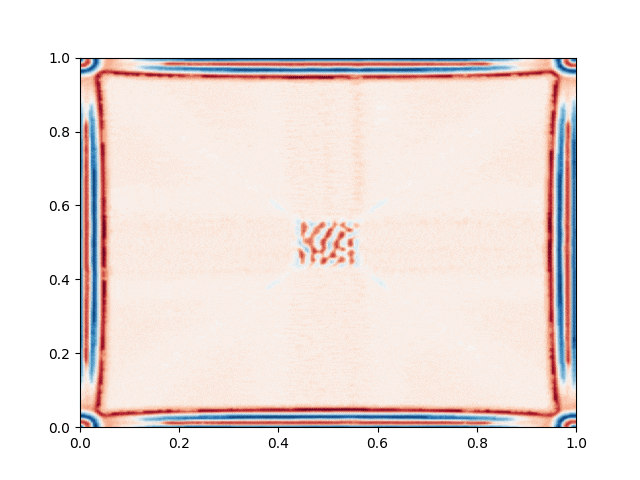
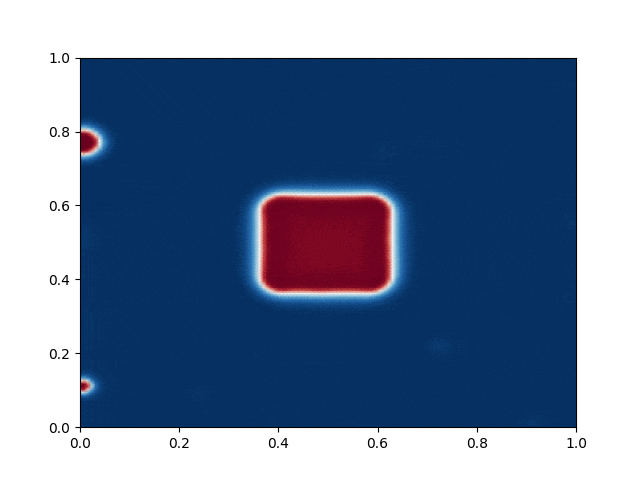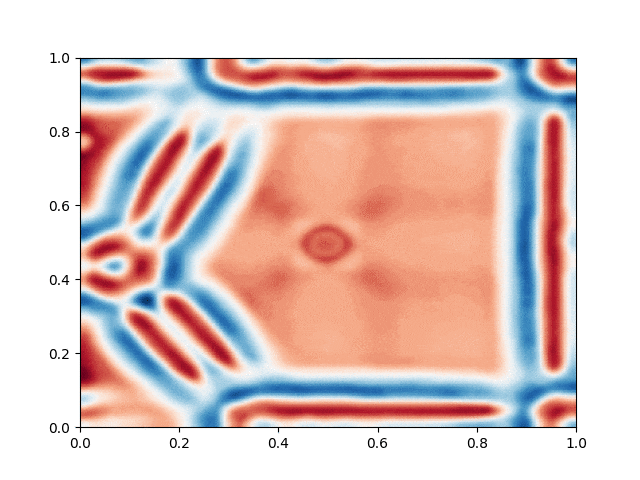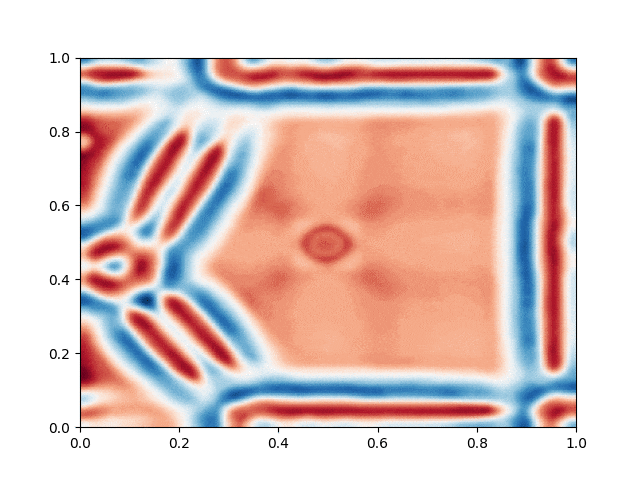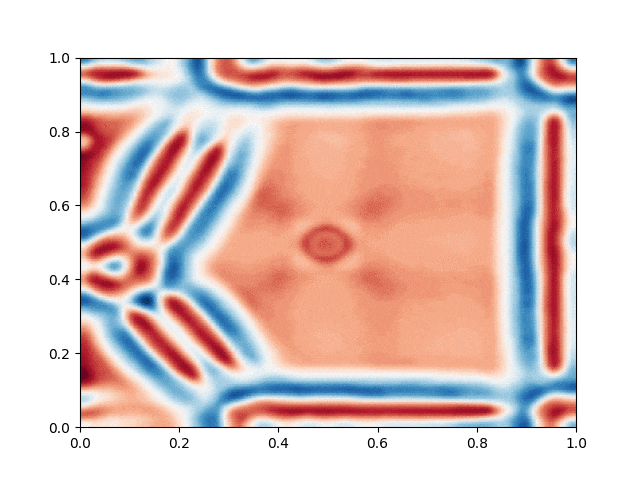
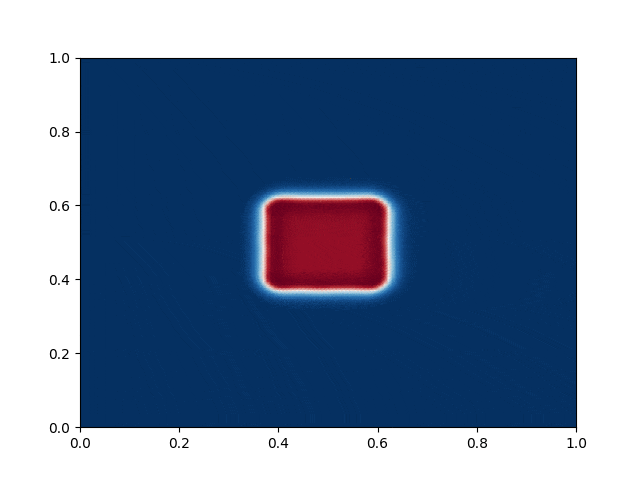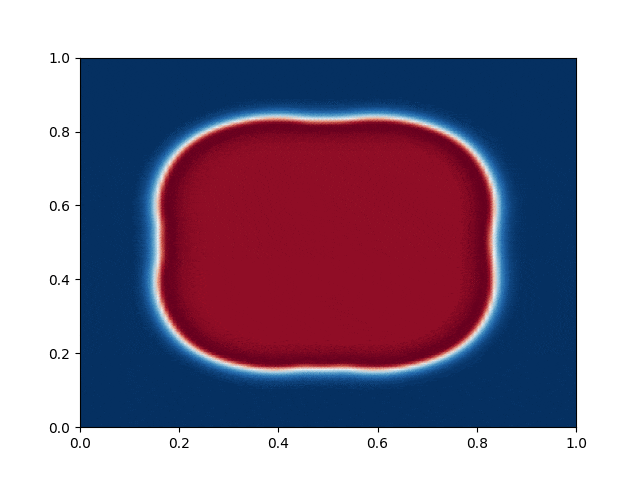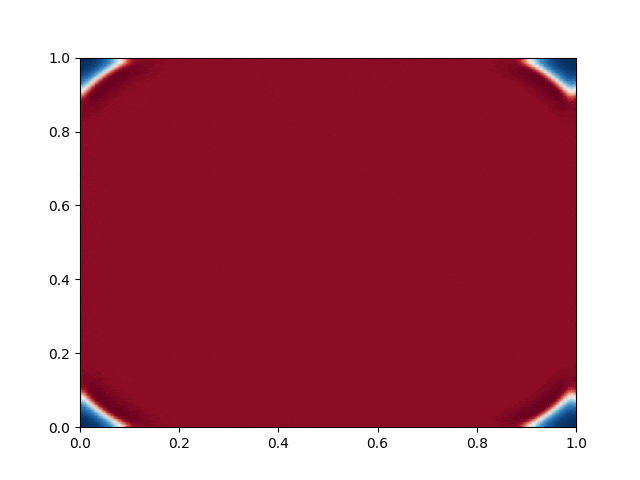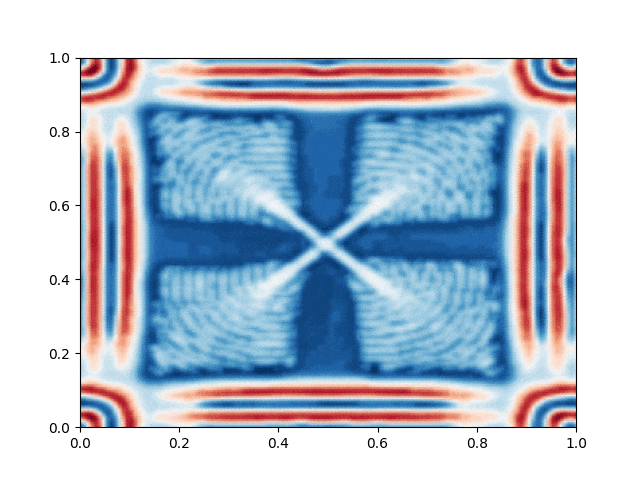
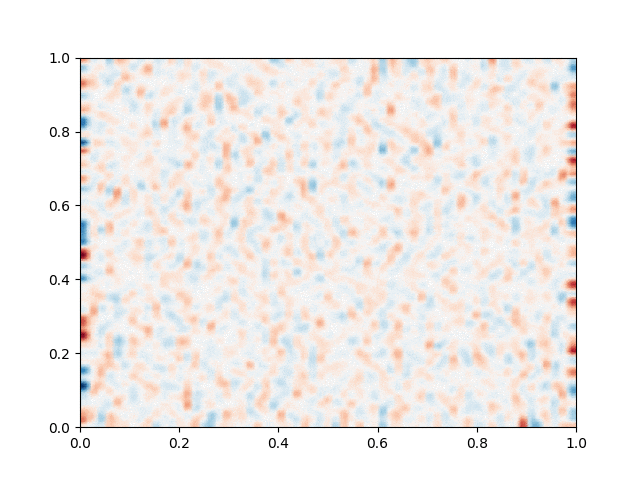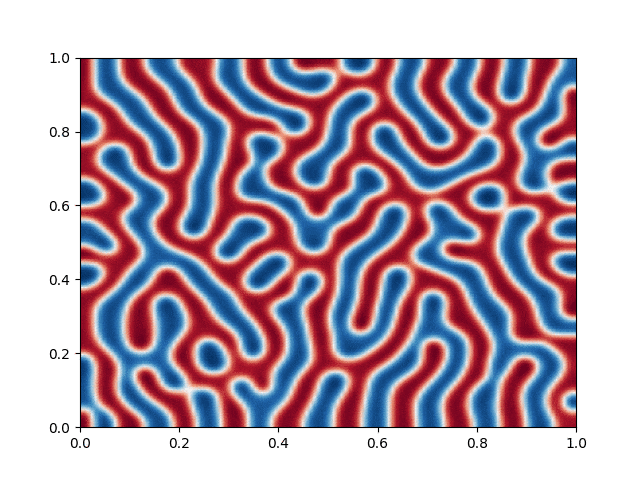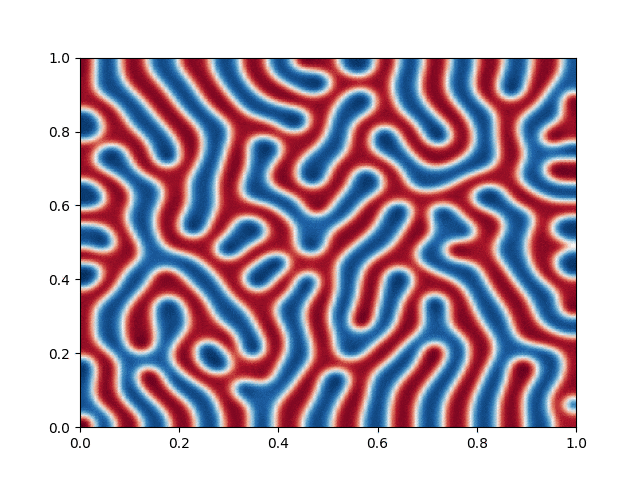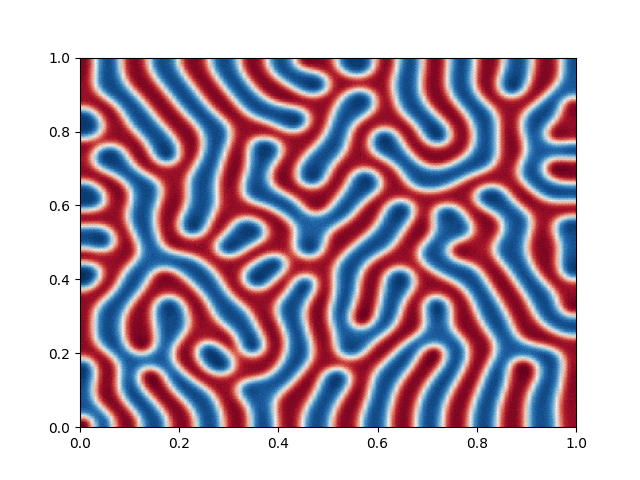
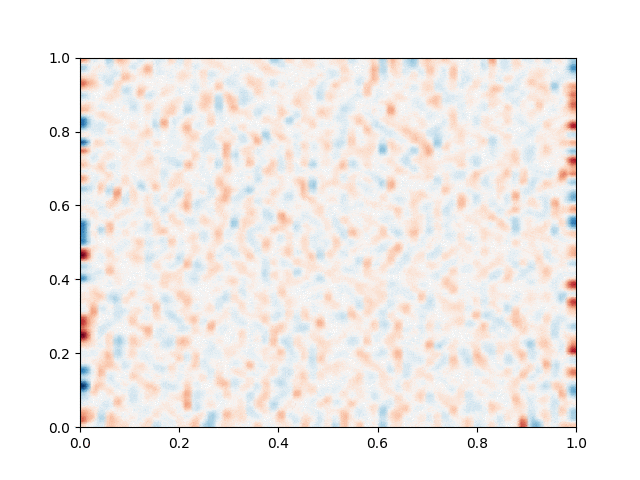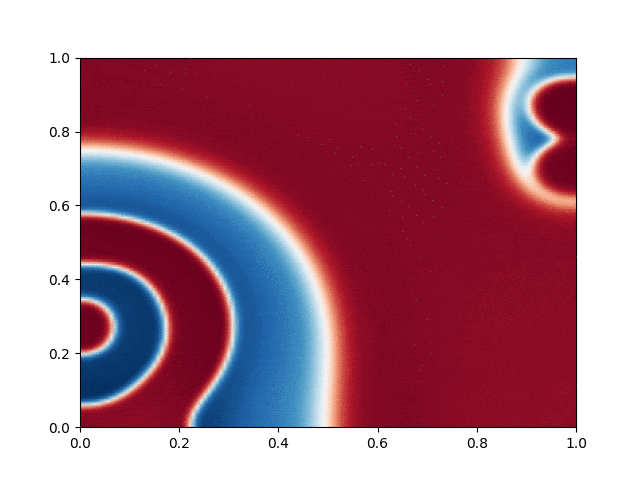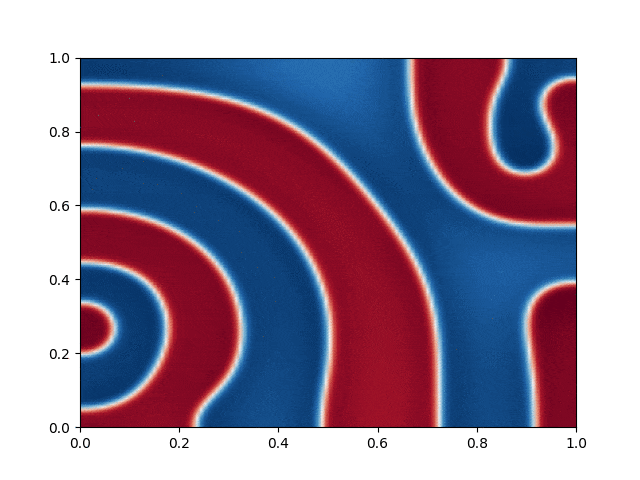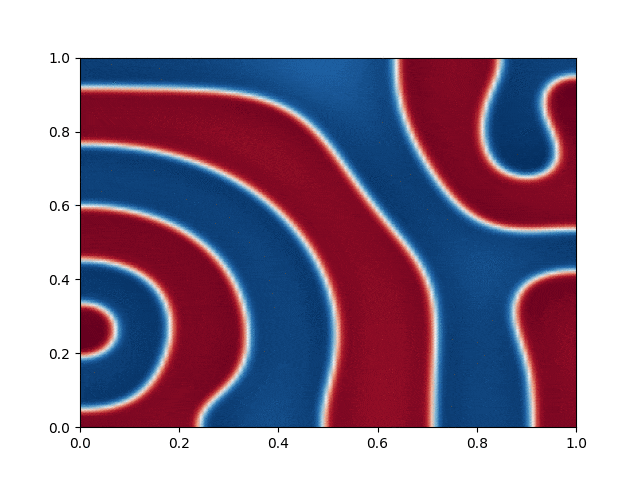
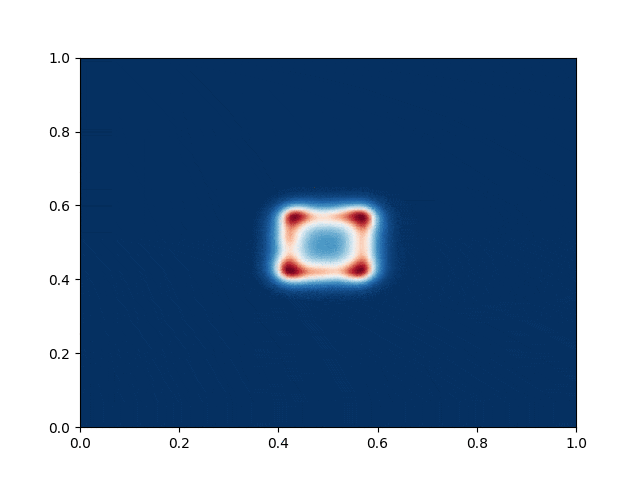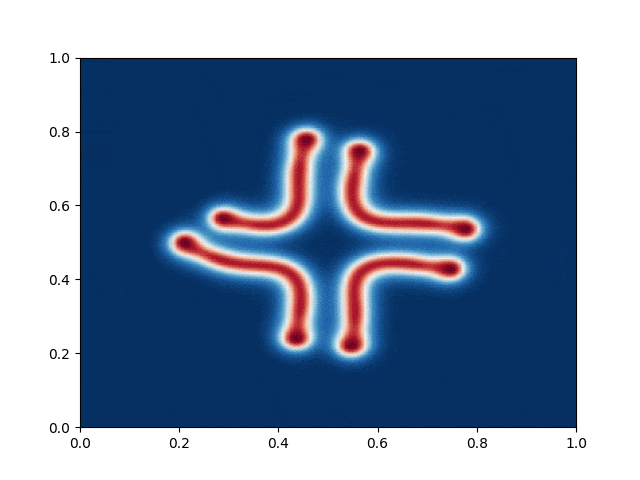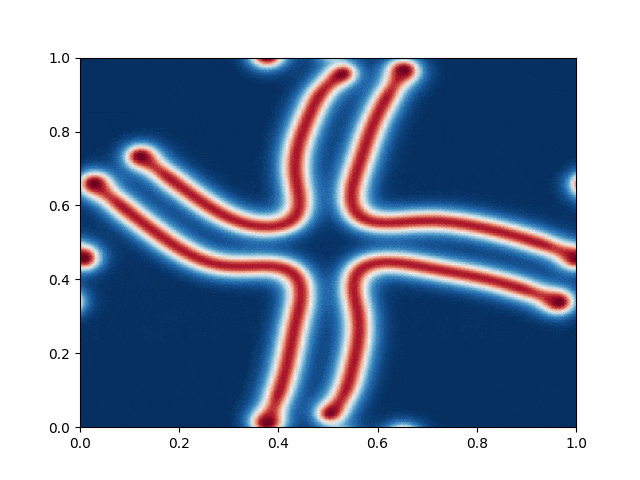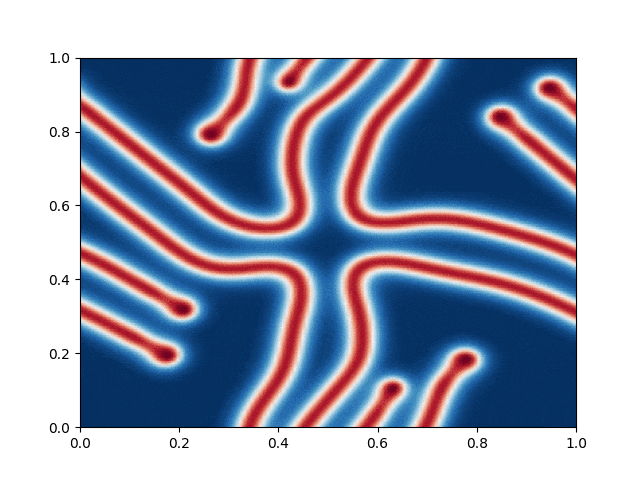
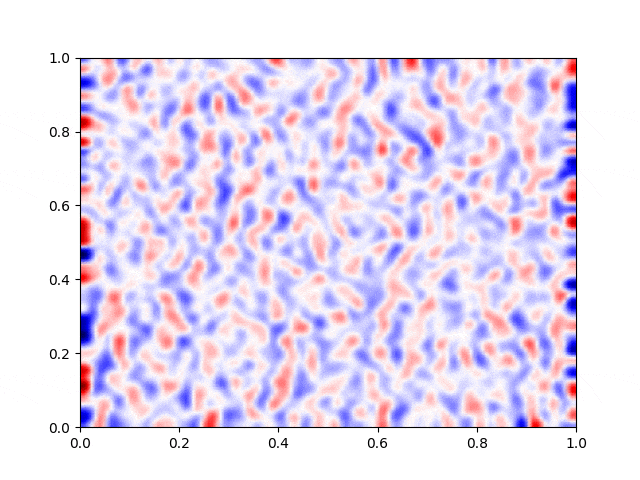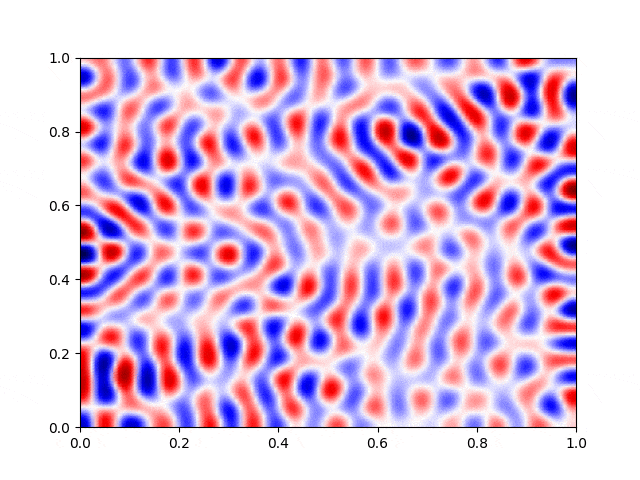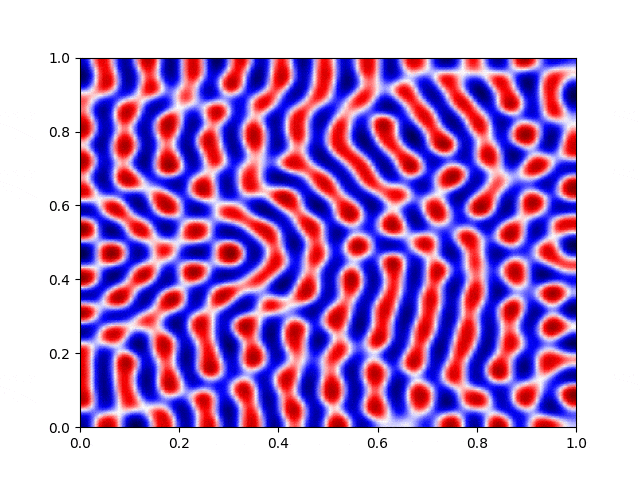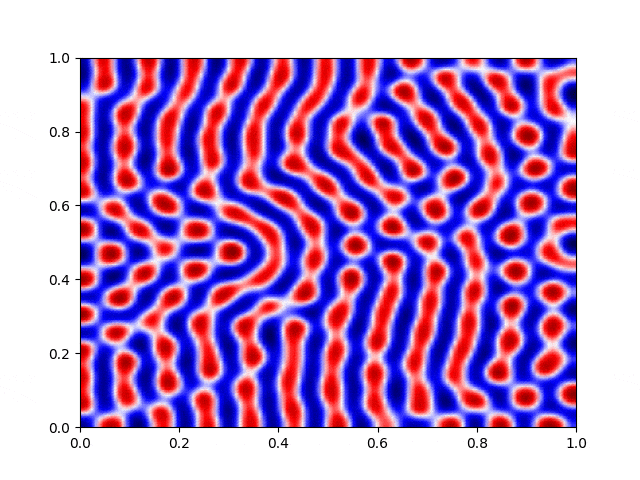
I made a python script that calls the C++ executable and gather the numerical results and produce the color plot animation. I saved the resulting GIFs, which are shown below: