This repository contains some basic code for using stochastic models in the form of Markov Chains.
For the time being the discount curve is given by a Nelson-Siegel or a Nelson-Svennson-Siegel model. A cubic spline implementation is although straightforward and recommended.
A hard-coded day counting convention of ACT/365 is used. A DayCounter object should be created for keeping track of the relevant information.
I provided a minimal set of Unit Tests to verify that the models match the respective closed formula, and that they produce exactly the same discount factor as the one from the input curve.
The Curve library provides the interface DiscountCurve, which is inherited by the chosen curve model, e.g. Nelson-Siegel. The DiscountCurve interface expects that the curve model implements the SpotRate method.
The NumericalLibrary module provides an Optimizer, which is just a wrapper of scipy minimizers. For single-dimension problem brent_method should generally work, as it is paired with a root bracketing algorithm, inspired by the golden ratio method.
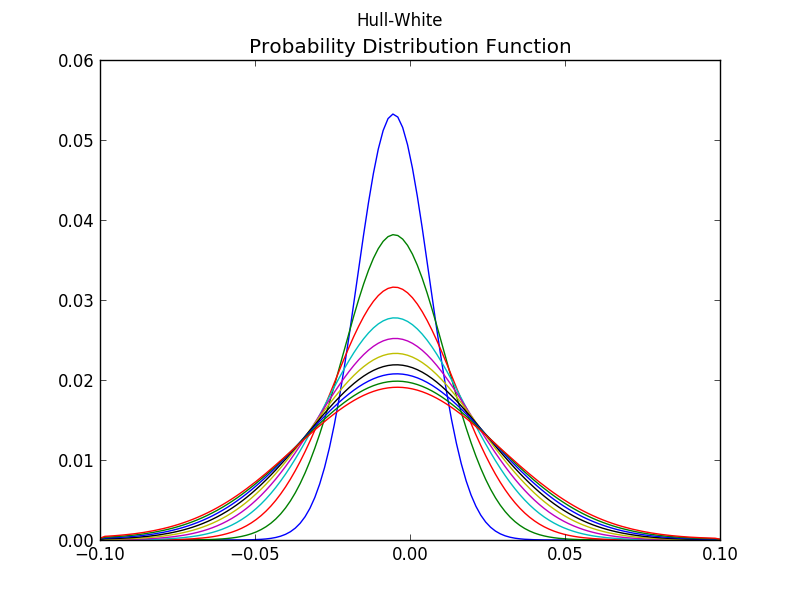
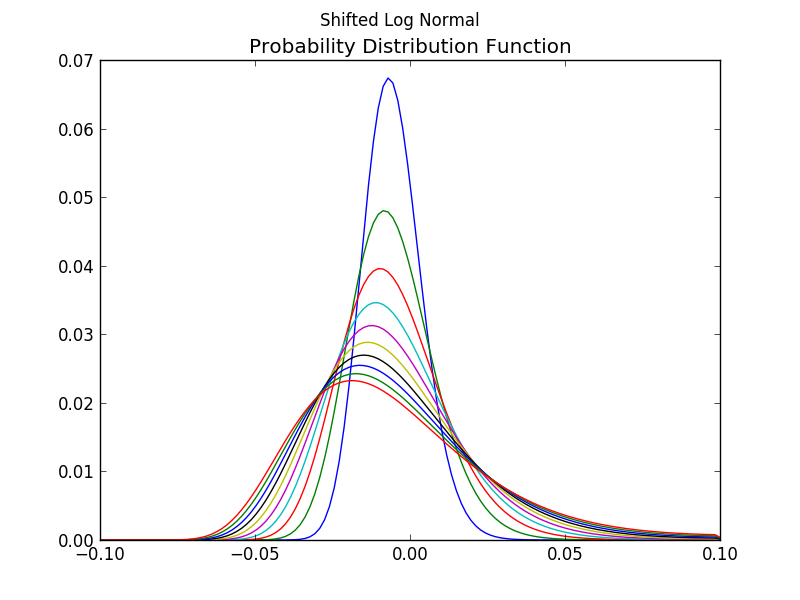
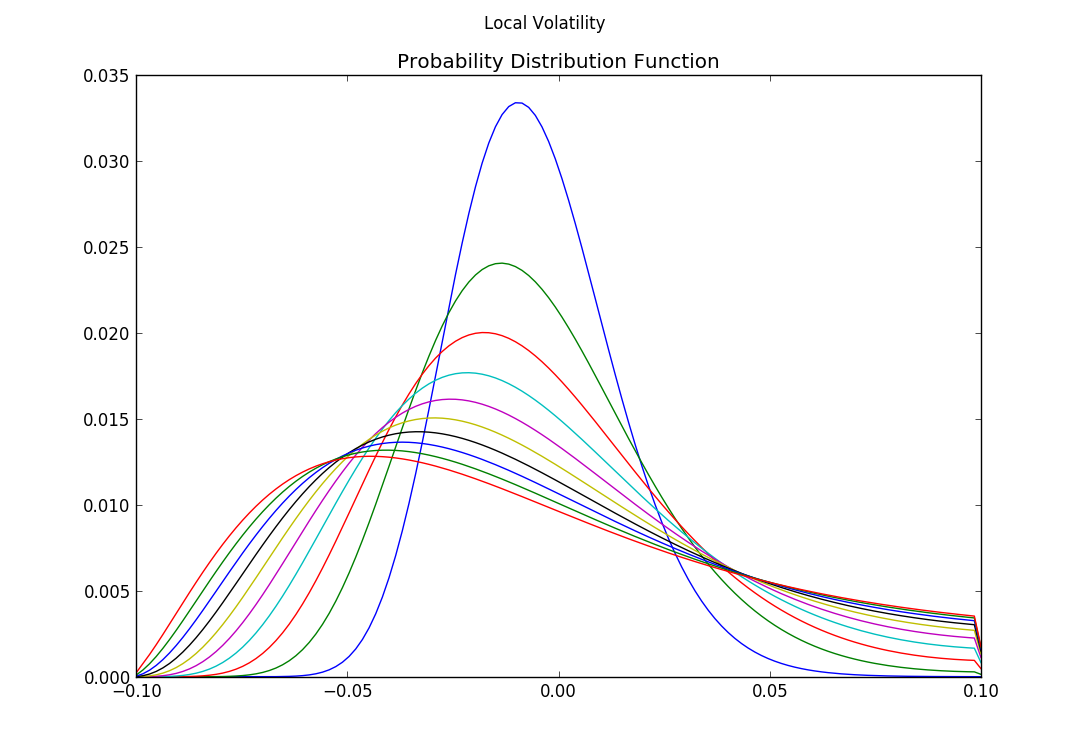
The StochasticModels library is the core of this repo. Its submodule ClosedFormModels contains the usual formulae found in every text book for Black-Scholes and Hull-White. The LatticeModels submodule contains the relevant code.
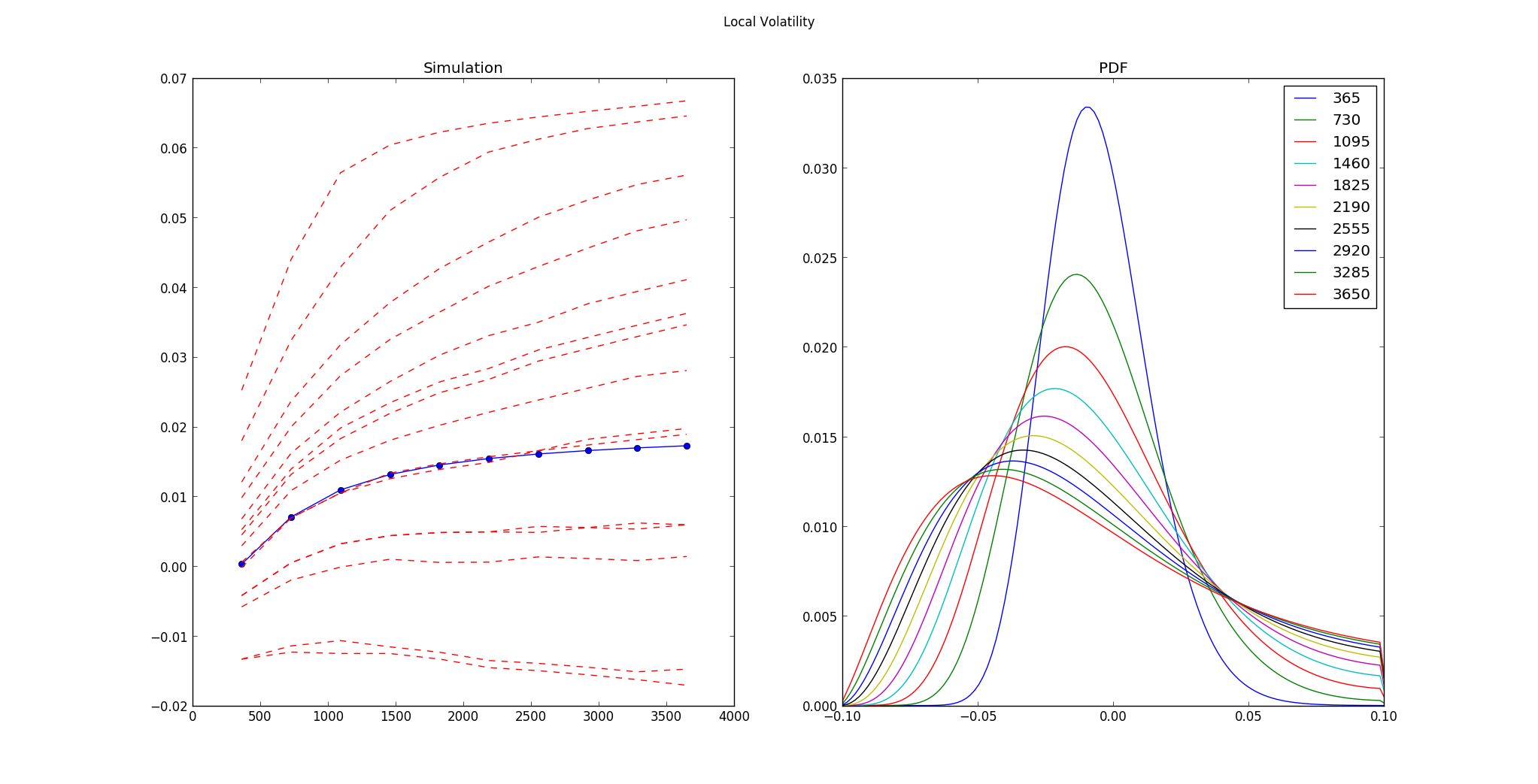
The main.py function stochastic_model_sk can be run for producing the following output:
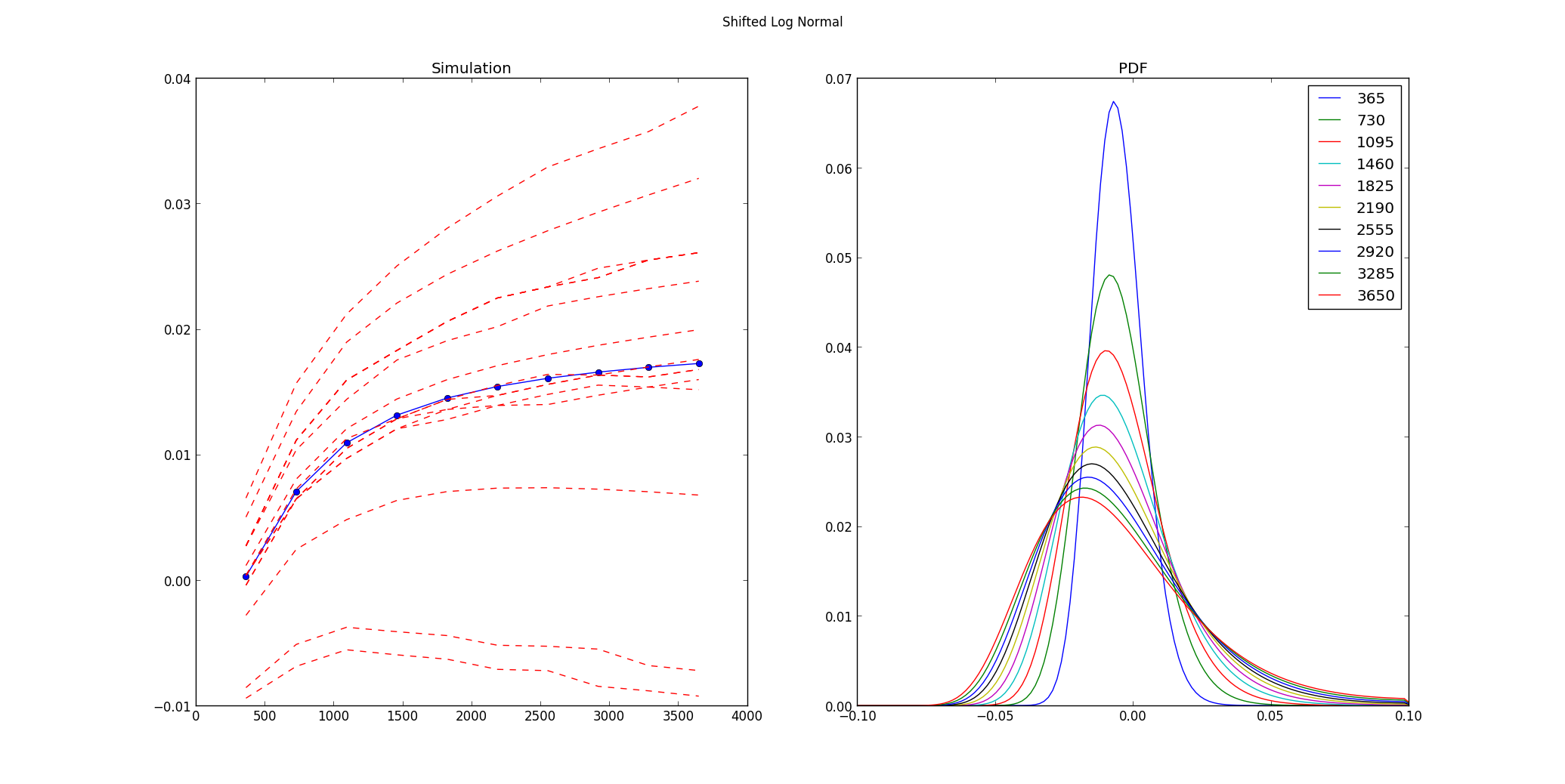
The MonteCarloModels module solves the Stochastic Differential Equation associated with the model in a more accurate way than the usual discretization. Since in this framework we are able to calculate the CDF with virtually no effort, we can generate uniform number in [0, 1] and find the inverse CDF. In this way is possible to have a simulated path that distributes according to the model PDF.
The main.py function monte_carlo_simulation can be run for producing the following output: