Doc and Vignettes updates

1. Doc updates.
2 Add a BO vignette.

.Rbuildignore

@@ -16,4 +16,5 @@
 ^vignettes/linked_DGP.Rmd$
 ^vignettes/seq_design.Rmd$
 ^vignettes/seq_design_2.Rmd$
+^vignettes/bayes_opt.Rmd$
 ^LICENSE\.md$

R/serialization.R

@@ -14,8 +14,9 @@
 #'
 #' @details See further examples and tutorials at <`r get_docs_url()`>.
 #' @note Since the constructed emulators are 'python' objects, they cannot be directly exported to other R processes for parallel
-#'     processing in multi-session workers. This function provides a way to convert the emulators into serialized objects, which can be
-#'     restored using [deserialize()] for multi-session processing.
+#'    processing in multi-session workers created through spawning. This function provides a solution by converting the emulators
+#'    into serialized objects, which can be restored using [deserialize()] for multi-session processing. Note that in forking,
+#'    serialization is generally not required.
 #' @examples
 #' \dontrun{
 #'
@@ -113,6 +114,7 @@ serialize <- function(object, light = TRUE) {
 #' @return The S3 class of a GP emulator, a DGP emulator, a linked (D)GP emulator, or a bundle of (D)GP emulators.
 #'
 #' @details See further examples and tutorials at <`r get_docs_url()`>.
+#' @note See the *Note* section in [serialize()].
 #' @examples
 #' \dontrun{
 #'

_pkgdown.yml

@@ -23,47 +23,24 @@ development:
   mode: auto
 
 articles:
-- title: DGP Emulation with the Heteroskedastic Gaussian Likelihood
-  desc: DGP modeling of the motorcycle accident data.
-  navbar: ~
-  contents:
-  - motorcycle
-
 - title: A Quick Guide to dgpsi
-  desc: A quick guide to dgpsi by emulating a step function.
+  desc: A quick introduction to dgpsi by emulating a step function.
   navbar: ~
   contents:
   - dgpsi
 
-- title: Linked (D)GP Emulation
-  desc: Linked (D)GP emulation of a synthetic system of three linked computer models.
+- title: A Deep Dive to dgpsi
+  desc: >
+    These articles provide an in-depth exploration of dgpsi and its diverse capabilities.
   navbar: ~
   contents:
+  - large_scale_emulation
   - linked_DGP
-
-- title: Sequential Design I
-  desc: Sequential design and dynamic pruning for the DGP emulator of a non-stationary simulator.
-  navbar: ~
-  contents:
+  - motorcycle
+  - classification
   - seq_design
-
-- title: Sequential Design II
-  desc: Sequential design for a bundle of DGP emulators with a stopping rule.
-  navbar: ~
-  contents:
   - seq_design_2
-
-- title: Large-scale Emulation with the Vecchia Approximation
-  desc: Large-scale DGP emulation using a Vecchia implementation under the SI.
-  navbar: ~
-  contents:
-  - large_scale_emulation
-
-- title: DGP Classification using dgpsi
-  desc: DGP classification of the iris data set.
-  navbar: ~
-  contents:
-  - classification
+  - bayes_opt
 
 reference:
 - title: "Initalization"

vignettes/bayes_opt.Rmd

@@ -0,0 +1,258 @@
+---
+title: "Customized Sequential Design for Bayesian Optimization"
+output: rmarkdown::html_vignette
+bibliography: references.bib 
+description: >
+  Customized sequential design to implement Bayesian optimization for the Shubert function.
+vignette: >
+  %\VignetteIndexEntry{Customized Sequential Design for Bayesian Optimization}
+  %\VignetteEngine{knitr::rmarkdown}
+  %\VignetteEncoding{UTF-8}
+---
+
+```{r setup, include = FALSE}
+knitr::opts_chunk$set(
+  echo = TRUE,
+  eval = FALSE
+)
+```
+
+This vignette demonstrates how to utilize and repurpose my favorite `design()` function in `dgpsi` to implement Bayesian optimization using the (D)GP surrogate models provided by the package.
+
+## Load the packages
+
+```{r}
+library(tidyverse)
+library(lhs)
+library(patchwork)
+library(ggplot2)
+library(dgpsi)
+```
+
+## Define the target function
+
+We consider a version of the Shubert function [@surjanovic] defined over the domain $[0,1]^2$ as follows:
+
+```{r}
+shubert <- function(x)
+{
+  N <- nrow(x)
+  x1 <- x[,1] * 4 - 2
+  x2 <- x[,2] * 4 - 2
+  ii <- c(1:5)
+  
+  y <- sapply(1:N, function(i) {
+    sum(ii * cos((ii+1)*x1[i]+ii)) * sum(ii * cos((ii+1)*x2[i]+ii))
+    })
+  
+  y <- matrix(y, ncol = 1)
+  return(y)
+}
+```
+
+To pass the Shubert function to `design()`, we defined it such that both its input `x` and output are matrices. Next, we generate the contour of the Shubert function:
+
+```{r}
+x1 <- seq(0, 1, length.out = 200)
+x2 <- seq(0, 1, length.out = 200)
+dat <- expand_grid(x1 = x1, x2 = x2)
+dat <- mutate(dat, f = shubert(cbind(x1, x2)))
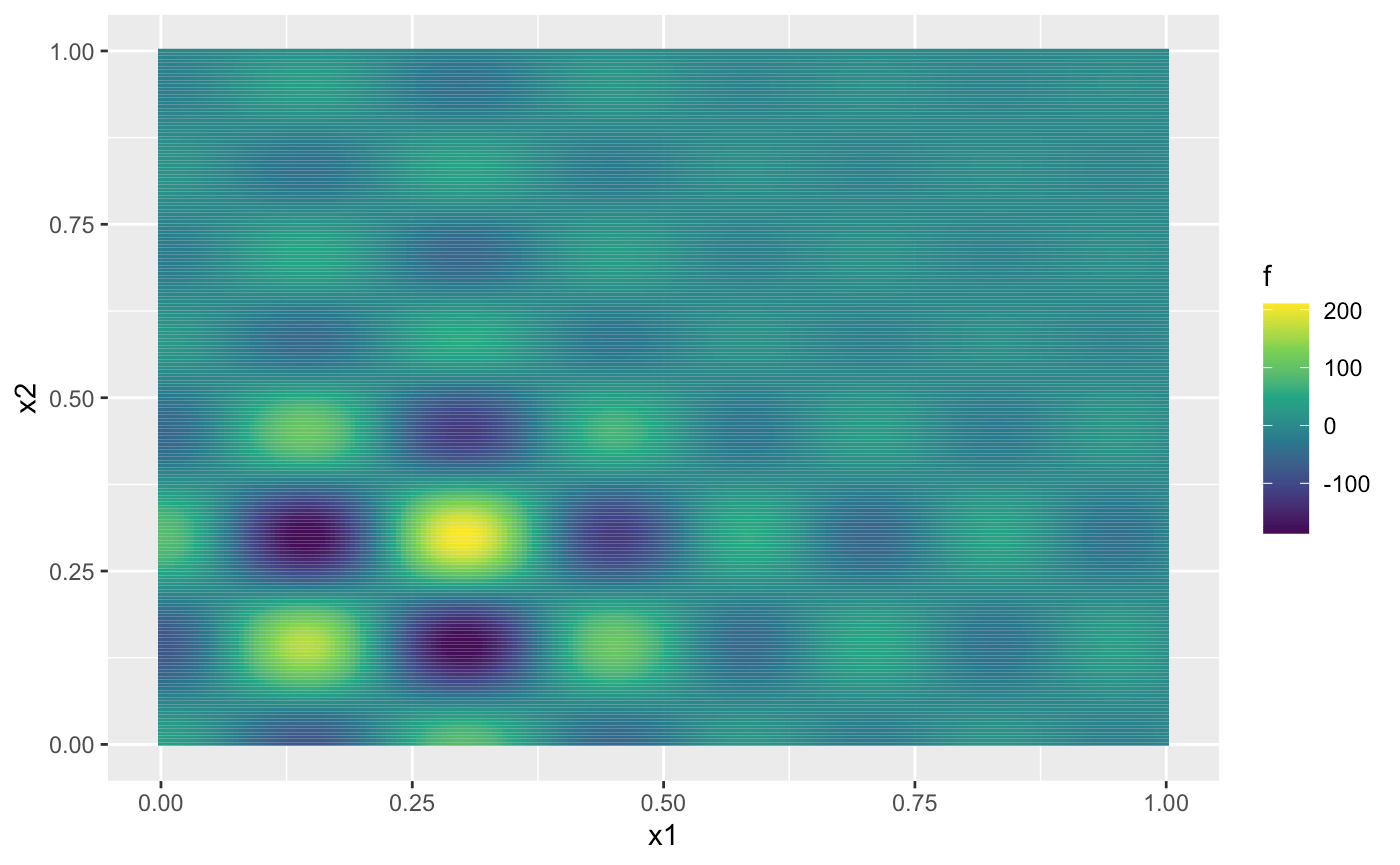
+ggplot(dat, aes(x1, x2, fill = f)) + geom_tile() + 
+  scale_fill_continuous(type = "viridis")
+```
+
+![](https://raw.githubusercontent.com/mingdeyu/dgpsi-R/master/vignettes/images/shubert.png){width=100%}
+
+From the figure above, we can observe that the Shubert function has several local minima and two global minima located at $(0.1437, 0.2999)$ and $(0.2999, 0.1437)$, both with values around $-186.7309$. In the remainder of this vignette, we will use Expected Improvement (EI) as the acquisition function to identify the global minima.
+
+## Initial emulator construction
+
+To ensure the reproducibility of this vignette, we set a seed using the `set_seed()` function from the package:
+
+```{r}
+set_seed(99)
+```
+
+Next, we generate an initial design of 20 points using the maximin Latin hypercube sampler:
+
+```{r}
+X <- maximinLHS(20, 2)
+Y <- shubert(X)
+```
+
+to construct the initial DGP surrogate model of the Shubert function:
+
+```{r}
+m <- dgp(X, Y, name = 'matern2.5')
+```
+
+```
+## Auto-generating a 2-layered DGP structure ... done
+## Initializing the DGP emulator ... done
+## Training the DGP emulator: 
+## Iteration 500: Layer 2: 100%|██████████| 500/500 [00:02<00:00, 249.19it/s]
+## Imputing ... done
+```
+
+## Bayesian optimization using Expected Improvement (EI)
+
+To begin Bayesian optimization with `design()`, we first need to define the Expected Improvement (EI) acquisition function, adhering to the rules specified for the `method` argument in `design()`:
+
+```{r}
+ei <- function(object, limits, n_starts = 10, ...) {
+  # Expected Improvement (EI) function
+  ei_function <- function(x) {
+    x <- matrix(x, nrow = 1)
+    # Extract mean and variance from the 'object'
+    pred <- predict(object, x, ...)$results
+    mu <- pred$mean
+    sigma <- sqrt(pred$var)
+    
+    # Handle numerical precision issues with very small sigma values
+    sigma[sigma < 1e-10] <- 1e-10
+    
+    # Best observed minimum value
+    best_value <- min(object$data$Y)
+    
+    # Calculate improvement
+    improvement <- best_value - mu
+    
+    # Calculate Expected Improvement (EI)
+    z <- improvement / sigma
+    ei <- improvement * pnorm(z) + sigma * dnorm(z)
+    ei <- ifelse(ei < 0, 0, ei)  # Ensure non-negative EI
+    
+    return(-ei)  # Return negative EI because `optim()` minimizes by default
+  }
+  
+  # Number of input dimensions
+  num_dims <- nrow(limits)
+  
+  # Generate initial points using Latin Hypercube Sampling (LHS)
+  lhd_samples <- maximinLHS(n_starts, num_dims)
+  lhd_points <- sapply(1:num_dims, function(i) {
+    limits[i, 1] + lhd_samples[, i] * (limits[i, 2] - limits[i, 1])
+  })
+  
+  # Perform optimization with multiple starts using `optim()`
+  results <- lapply(1:n_starts, function(i) {
+    optim(
+      par = lhd_points[i, ],
+      fn = ei_function,
+      method = "L-BFGS-B",
+      lower = limits[, 1],
+      upper = limits[, 2]
+    )
+  })
+  
+  # Find the result with the minimum (most negative) EI
+  best_result <- results[[which.min(sapply(results, `[[`, "value"))]]
+  
+  # Return the next best point `x` as a single-row matrix
+  return(matrix(best_result$par, nrow = 1))
+}
+
+```
+
+The `ei` function defined above takes the emulator as its first argument, `object`, along with the additional arguments: `limits`, a two-column matrix where the first column specifies the lower bounds and the second column specifies the upper bounds of the input dimensions, and `n_starts`, which defines the number of multi-start points used to search for the location corresponding to the minimum (most negative) EI. You can, of course, replace `ei` with your own acquisition function, provided it adheres to the rules of the `method` argument in `design()` (see `?design` for details).
+
+To track the identified minimum value of the Shubert function during Bayesian optimization, we define a monitor function, `opt_monitor`, to be passed to the `eval` argument of `design()`:
+
+```{r}
+opt_monitor <- function(object) {
+  return(min(object$data$Y))
+}
+```
+
+The domain of the input parameters for our Bayesian optimization, within which the global minima are searched, is defined as $[0,1]^2$:
+
+```{r}
+lim <- rbind(c(0, 1), c(0, 1))
+```
+
+With all the ingredients ready, we can now run the Bayesian optimization using `design()` with 80 iterations:
+
+```{r}
+m <- design(m, N = 80, limits = lim, f = shubert, method = ei, eval = opt_monitor)
+```
+
+```
+## Initializing ... done
+##  * Metric: -125.203479
+## Iteration 1:
+##  - Locating ... done
+##  * Next design point: 0.352375 0.142570
+##  - Updating and re-fitting ... done
+##  - Validating ... done
+##  * Metric: -125.203479
+## 
+## ...
+## 
+## Iteration 6:
+##  - Locating ... done
+##  * Next design point: 0.299331 0.125606
+##  - Updating and re-fitting ... done
+##  - Transiting to a GP emulator ... done
+##  - Validating ... done
+##  * Metric: -186.039545
+## 
+## ...
+## 
+## Iteration 80:
+##  - Locating ... done
+##  * Next design point: 0.907645 0.000000
+##  - Updating and re-fitting ... done
+##  - Validating ... done
+##  * Metric: -186.728582
+```
+
+During the Bayesian optimization, our dynamic pruning mechanism transitioned the DGP emulator to a GP emulator at iteration 6, leading to faster optimizations in the remaining iterations while maintaining the emulator's quality. After 80 iterations, we identified a minimum of the Shubert function with a value of $-186.7286$, which is very close to the global minimum of $-186.7309$. We can inspect the progress of the minima search conducted by `design()` by applying `draw()` to `m`:
+
+```{r}
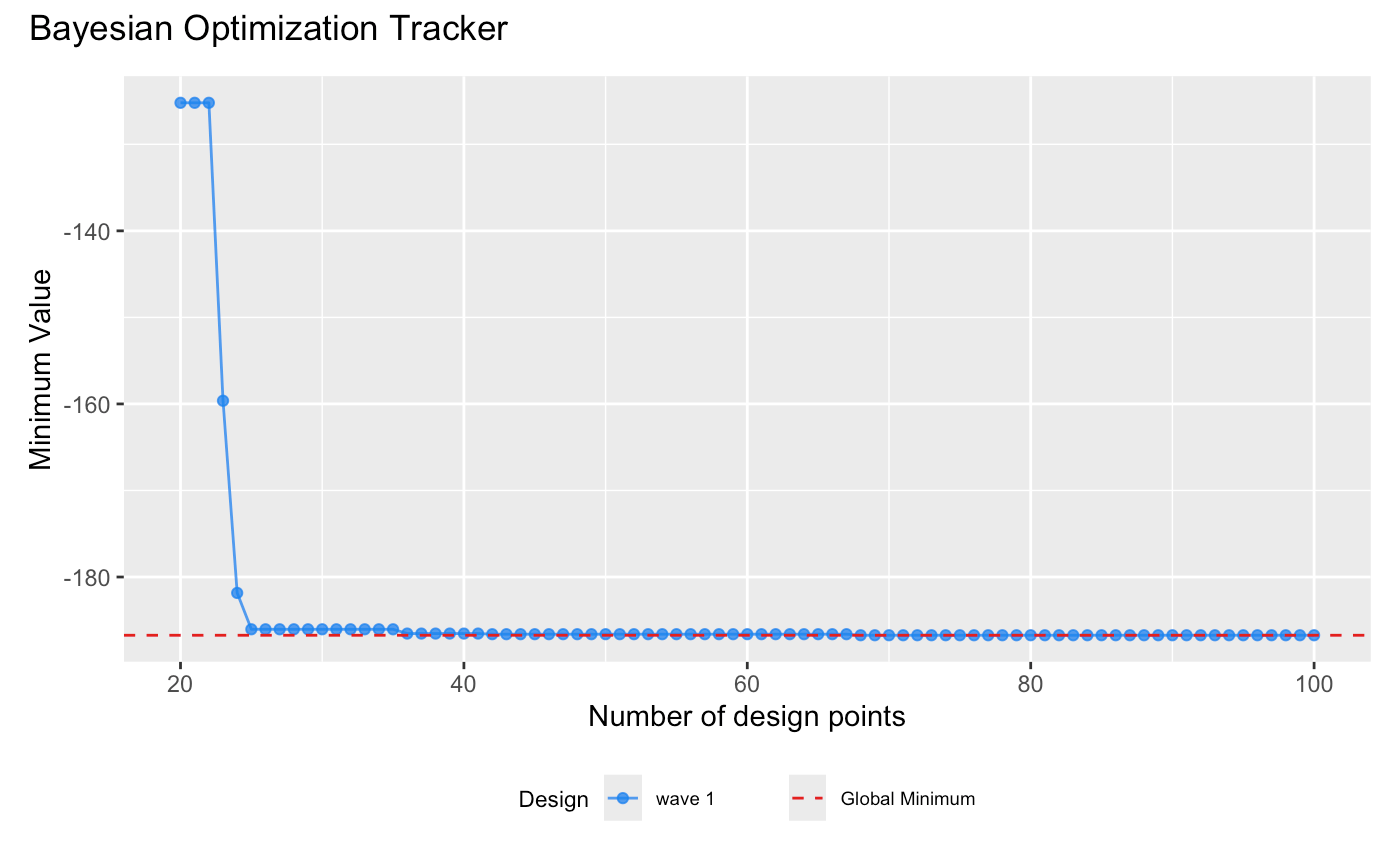
+draw(m) +
+  plot_annotation(title = 'Bayesian Optimization Tracker') +
+  labs(y = "Minimum Value") +
+  # Add a horizontal line to represent the global minimum for benchmarking
+  geom_hline(
+    aes(yintercept = y, linetype = "Global Minimum"), # Global minimum
+    data = data.frame(y = -186.7309),
+    color = "#E31A1C",
+    size = 0.5
+  ) +
+  scale_linetype_manual(
+    values = c("Global Minimum" = "dashed"),
+    name = "" # Remove the legend title
+  )
+```
+
+![](https://raw.githubusercontent.com/mingdeyu/dgpsi-R/master/vignettes/images/bo_tracker.png){width=100%}
+
+The figure above shows that Bayesian optimization using our (D)GP emulator quickly identifies a low value of the Shubert function within 5 iterations. Notably, the lowest value, $-186.7286$, was achieved by `design()` after 48 iterations.
+
+We can also inspect the locations identified during the process by applying `draw()` to `m` with `type = 'design'`:
+
+```{r}
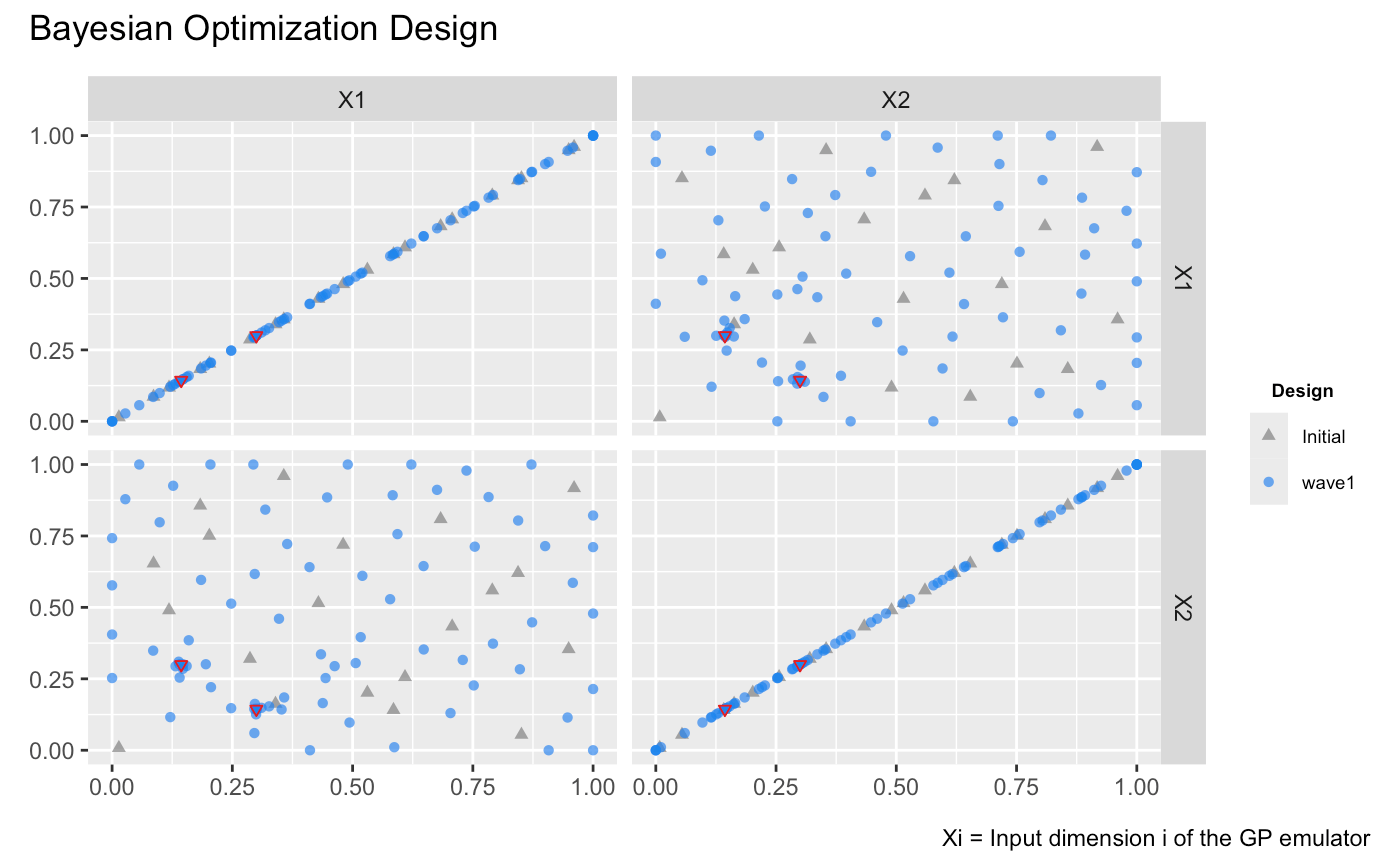
+draw(m, type = 'design') + 
+  plot_annotation(title = 'Bayesian Optimization Design') +
+  # Highlight the global minima on the design plot
+  geom_point(
+    data = data.frame(
+      .panel_x = c("X1", "X2"),  # x labels of panels
+      .panel_y = c("X2", "X1"),  # y labels of panels
+      X1 = c(0.1437, 0.2999),    # X1 values for the global minima
+      X2 = c(0.2999, 0.1437)     # X2 values for the global minima
+    ),
+    aes(x = .panel_x, y = .panel_y),
+    size = 1.25, 
+    shape = 6,
+    color = "#E31A1C"           
+  )
+```
+
+![](https://raw.githubusercontent.com/mingdeyu/dgpsi-R/master/vignettes/images/bo_design.png){width=100%}
+
+The figure above illustrates that Bayesian optimization successfully identifies the regions around the two global minima, represented as red inverted triangles, by adding design points concentrated near these two locations.
+
+### References
+
+

vignettes/dgpsi.Rmd

@@ -30,7 +30,7 @@ get_article_url <- function(article) {
 }
 ```
 
-The `dgpsi` package offers a flexible toolbox for Gaussian process (GP), deep Gaussian process (DGP), and linked (D)GP emulation. In this guide, we show how to use the package to emulate a step function using a three-layered DGP structure. Additional examples showcasing the package's functionality are available in the [Articles](`r get_article_url("/articles/index.html")`) section of the package website. Topics include [linked DGPs](`r get_article_url("/articles/linked_DGP.html")`), [scalable DGPs](`r get_article_url("/articles/large_scale_emulation.html")`), [DGPs for classification](`r get_article_url("/articles/classification.html")`), [non-Gaussian problems](`r get_article_url("/articles/motorcycle.html")`), and [sequential design and active learning for DGPs](`r get_article_url("/articles/seq_design.html")`). A detailed reference for all available functions is provided in the [Reference](`r get_article_url("/reference/index.html")`) section of the package website.
+The `dgpsi` package offers a flexible toolbox for Gaussian process (GP), deep Gaussian process (DGP), and linked (D)GP emulation. In this guide, we show how to use the package to emulate a step function using a three-layered DGP structure. Additional examples showcasing the package's functionality are available in the [Articles](`r get_article_url("/articles/index.html")`) section of the package website. Topics include [linked DGPs](`r get_article_url("/articles/linked_DGP.html")`), [scalable DGPs](`r get_article_url("/articles/large_scale_emulation.html")`), [DGPs for classification](`r get_article_url("/articles/classification.html")`), [non-Gaussian problems](`r get_article_url("/articles/motorcycle.html")`), [sequential design and active learning for (D)GPs](`r get_article_url("/articles/seq_design.html")`), and [Bayesian optimization with (D)GPs](`r get_article_url("/articles/bayes_opt.html")`). A detailed reference for all available functions is provided in the [Reference](`r get_article_url("/reference/index.html")`) section of the package website.
 
 ## Load the package
 

vignettes/references.bib

@@ -25,3 +25,10 @@ @article{anderson1935irises
   pages={2--5},
   year={1935}
 }
+
+@misc{surjanovic,
+  author       = {Surjanovic, Simon and  Bingham, Derek},
+  title        = {Virtual Library of Simulation Experiments: Test Functions and Datasets},
+  howpublished = {\url{https://www.sfu.ca/~ssurjano/index.html}},
+  note         = {Accessed: 13 December, 2024}
+}