qtl2pleio is a software package for use with the R statistical
computing environment. qtl2pleio is
freely available for download and use. I share it under the MIT
license. The user will
also want to download and install the qtl2 R
package.
Click
here
to explore qtl2pleio within a live Rstudio
session in “the cloud”.
We eagerly welcome contributions to qtl2pleio. All pull requests will
be considered. Features requests and bug reports may be filed as Github
issues. All contributors must abide by the code of
conduct.
For technical support, please open a Github issue. If you’re just
getting started with qtl2pleio, please examine the
vignettes on the package’s web
site. You can also email
[email protected] for assistance.
The goal of qtl2pleio is, for a pair of traits that show evidence for
a QTL in a common region, to distinguish between pleiotropy (the null
hypothesis, that they are affected by a common QTL) and the alternative
that they are affected by separate QTL. It extends the likelihood ratio
test of Jiang and Zeng
(1995) for
multiparental populations, such as Diversity Outbred mice, including the
use of multivariate polygenic random effects to account for population
structure. qtl2pleio data structures are those used in the
rqtl/qtl2 package.
To install qtl2pleio, use install_github() from the
devtools package.
install.packages("qtl2pleio")You may also wish to install the R/qtl2. We will use it below.
install.packages("qtl2")Below, we walk through an example analysis with Diversity Outbred mouse
data. We need a number of preliminary steps before we can perform our
test of pleiotropy vs. separate QTL. Many procedures rely on the R
package qtl2. We first load the qtl2 and qtl2pleio packages.
library(qtl2)
library(qtl2pleio)
library(ggplot2)We’ll consider the
DOex data in the
qtl2data repository. We’ll
download the DOex.zip file before calculating founder allele dosages.
file <- paste0("https://raw.githubusercontent.com/rqtl/",
"qtl2data/master/DOex/DOex.zip")
DOex <- read_cross2(file)probs <- calc_genoprob(DOex)Let’s calculate the founder allele dosages from the 36-state genotype probabilities.
pr <- genoprob_to_alleleprob(probs)We now have an allele probabilities object stored in pr.
names(pr)
#> [1] "2" "3" "X"
dim(pr$`2`)
#> [1] 261 8 127We see that pr is a list of 3 three-dimensional arrays - one array for
each of 3 chromosomes.
For our statistical model, we need a kinship matrix. We get one with the
calc_kinship function in the rqtl/qtl2 package.
kinship <- calc_kinship(probs = pr, type = "loco")We use the multivariate linear mixed effects model:
vec(Y) = Xvec(B) + vec(G) + vec(E)
where Y contains phenotypes, X contains founder allele probabilities and covariates, and B contains founder allele effects. G is the polygenic random effects, while E is the random errors. We provide more details in the vignette.
The function to simulate phenotypes in qtl2pleio is sim1.
# set up the design matrix, X
pp <- pr[[2]] #we'll work with Chr 3's genotype data#Next, we prepare a design matrix X
X <- gemma2::stagger_mats(pp[ , , 50], pp[ , , 50])# assemble B matrix of allele effects
B <- matrix(data = c(-1, -1, -1, -1, 1, 1, 1, 1, -1, -1, -1, -1, 1, 1, 1, 1), nrow = 8, ncol = 2, byrow = FALSE)
# set.seed to ensure reproducibility
set.seed(2018-01-30)
Sig <- calc_Sigma(Vg = diag(2), Ve = diag(2), kinship = kinship[[2]])
# call to sim1
Ypre <- sim1(X = X, B = B, Sigma = Sig)
Y <- matrix(Ypre, nrow = 261, ncol = 2, byrow = FALSE)
rownames(Y) <- rownames(pp)
colnames(Y) <- c("tr1", "tr2")Let’s perform univariate QTL mapping for each of the two traits in the Y matrix.
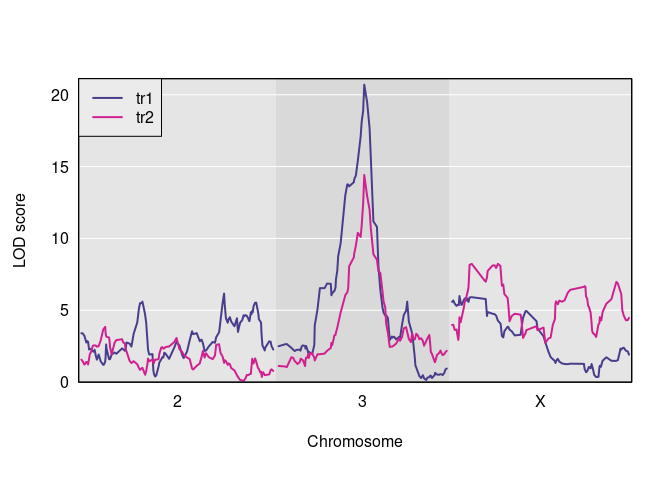
s1 <- scan1(genoprobs = pr, pheno = Y, kinship = kinship)Here is a plot of the results.
And here are the observed QTL peaks with LOD > 8.
find_peaks(s1, map = DOex$pmap, threshold=8)
#> lodindex lodcolumn chr pos lod
#> 1 1 tr1 3 82.77806 20.703383
#> 2 2 tr2 3 82.77806 14.417924
#> 3 2 tr2 X 48.10040 8.231551We now have the inputs that we need to do a pleiotropy vs. separate QTL
test. We have the founder allele dosages for one chromosome, i.e., Chr
3, in the R object pp, the matrix of two trait measurements in Y,
and a LOCO-derived kinship matrix, kinship[[2]].
out <- suppressMessages(scan_pvl(probs = pp,
pheno = Y,
kinship = kinship[[2]], # 2nd entry in kinship list is Chr 3
start_snp = 38,
n_snp = 25
))To visualize results from our two-dimensional scan, we calculate profile
LOD for each trait. The code below makes use of the R package ggplot2
to plot profile LODs over the scan region.
library(dplyr)
out %>%
calc_profile_lods() %>%
add_pmap(pmap = DOex$pmap$`3`) %>%
ggplot() + geom_line(aes(x = marker_position, y = profile_lod, colour = trait))We use the function calc_lrt_tib to calculate the likelihood ratio
test statistic value for the specified traits and specified genomic
region.
(lrt <- calc_lrt_tib(out))
#> [1] 0Before we call boot_pvl, we need to identify the index (on the
chromosome under study) of the marker that maximizes the likelihood
under the pleiotropy constraint. To do this, we use the qtl2pleio
function find_pleio_peak_tib.
(pleio_index <- find_pleio_peak_tib(out, start_snp = 38))
#> log10lik13
#> 50set.seed(2018-11-25) # set for reproducibility purposes.
b_out <- suppressMessages(boot_pvl(probs = pp,
pheno = Y,
pleio_peak_index = pleio_index,
kinship = kinship[[2]], # 2nd element in kinship list is Chr 3
nboot = 10,
start_snp = 38,
n_snp = 25
))(pvalue <- mean(b_out >= lrt))
#> [1] 1citation("qtl2pleio")
#>
#> To cite qtl2pleio in publications use:
#>
#> Boehm FJ, Chesler EJ, Yandell BS, Broman KW (2019) Testing pleiotropy
#> vs. separate QTL in multiparental populations G3
#> https://www.g3journal.org/content/9/7/2317
#>
#> A BibTeX entry for LaTeX users is
#>
#> @Article{Boehm2019testing,
#> title = {Testing pleiotropy vs. separate QTL in multiparental populations},
#> author = {Frederick J. Boehm and Elissa J. Chesler and Brian S. Yandell and Karl W. Broman},
#> journal = {G3},
#> year = {2019},
#> volume = {9},
#> issue = {7},
#> url = {https://www.g3journal.org/content/9/7/2317},
#> eprint = {https://www.g3journal.org/content/ggg/9/7/2317.full.pdf},
#> }