A demo repo to study on resource sharing algorithm in EDA, aimed to decrease the circuits' area.
We measured the compile result of Design Compiler, and find out that its resource sharing algorithm is greedy, which means it can't achieve a best sharing decision. For example:
// test.v
module top(input CLK,
input [31:0] a,
input [31:0] b,
input [31:0] c,
input [31:0] d,
input [31:0] e,
input [31:0] f,
input [1:0] state,
output reg[31:0] out
);
always @(posedge CLK) begin
if (state == 0) begin
o = a + b + c;
end
else if (state == 1) begin
o = a + b + d;
end
else begin
if (state == 2) begin
o = b + c + e;
end
else begin
o = c + e + f;
end
end
end
endmoduleif we manually do the resource sharing, it should be:
// test_manual.v
if (state == 0) begin
tmp1 = a;
tmp2 = b;
tmp3 = c;
end
else if (state == 1) begin
tmp1 = a;
tmp2 = b;
tmp3 = d;
end
else begin
if (state == 2) begin
tmp1 = e;
tmp2 = b;
tmp3 = c;
end
else begin
tmp1 = e;
tmp2 = f;
tmp3 = c;
end
end
o = tmp1 + tmp2 + tmp3and the result is, for every tmp, it only has to choose from two different input, which means it only needs a two input mux to choose value which needed the tmp reg to hold.
But to Design Compiler, it seems to choose to first share b and e (since 3 of 4 branches have the input b), and then share a and c, lastly share c,d,e,f.
The problem is, this sharing decision is apparently not the best one. it use 2 two input mux and 1 four input mux.
// part of test_mapped.v generated by design compiler
// share b and e
OAI21_X1 U476 ( .B1(n387), .B2(n394), .A(n490), .ZN(\U3/U2/Z_8 ) );
NAND2_X1 U477 ( .A1(b[8]), .A2(n489), .ZN(n490) );
INV_X1 U478 ( .A(e[8]), .ZN(n394) );
// share a and c
AOI22_X1 U374 ( .A1(c[1]), .A2(n353), .B1(a[1]), .B2(n354), .ZN(n384) );
// share e,c,d,f
INV_X1 U526 ( .A(e[21]), .ZN(n442) );
INV_X1 U430 ( .A(c[21]), .ZN(n443) );
OAI221_X1 U428 ( .B1(n388), .B2(n442), .C1(n443), .C2(n391), .A(n444), .ZN(
\U3/U3/Z_21 ) );
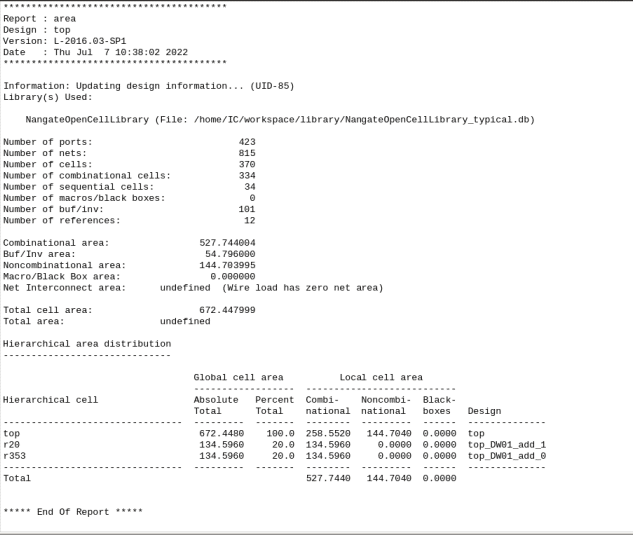
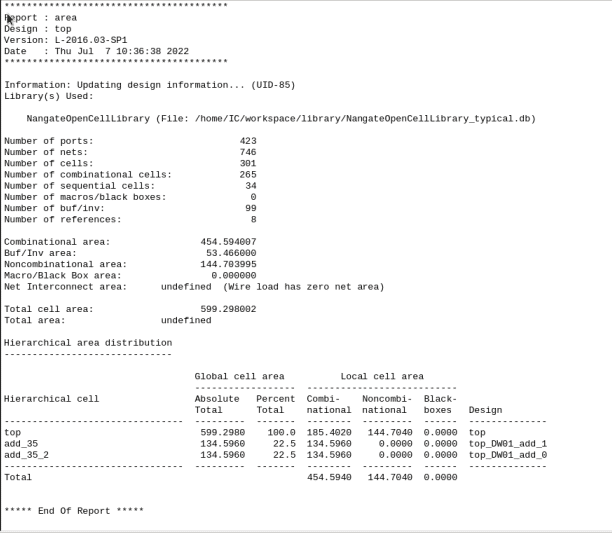
AOI22_X1 U429 ( .A1(d[21]), .A2(n351), .B1(f[21]), .B2(n393), .ZN(n444) );And we measured the area of those two type of resource sharing. We first let the Design compiler do a compile process to the origin code test.v, and then disable its resource sharing (use command set hlo_resource_allocation none) , and let it compile the test_manual.v. And we got those results: (former one is design compiler's resource sharing)
So, how to manual do this better resource sharing?
Take the following case as an example, before we start, make sure the equations do not have brackets:
branch1:
o = a + b - c * e;
branch2:
o = a - b * d + f;
branch3:
o = b - c + e * f;
branch4:
o = a + e * f - a;
Even though we know that plus operation is similar to minus operation, we still don't want to import more other operations (like use invert the input and plus one), which will increase the area. So we choose to preserve the operators, and 'align' those equations. Aligned equations should be like:
branch1:
o = a + b - c * e;
branch2:
o = a + f - b * d;
branch3:
o = b + e * f - c;
branch4:
o = a + e * f - a;
This indicates that for the output reg o, every branch includes one plus, one multiply and one minus operators. (Later we will discuss about the branches with different numbers of operators).
We first use share the multiply operations first (also discuss later), and it becomes:
branch1:
o = (a + b) - (tmp);
branch2:
o = (a + f) - (tmp);
branch3:
o = (b + tmp) - (c);
branch4:
o = (a + tmp) - (a);
reg tmp means the multiply results. And then, we can divide this code into two parts, in each part the operators only consists plus. And those parts do resource sharing seperately.
For the first part, it looks like:
branch1:
o1 = (a + b)
branch2:
o1 = (a + f)
branch3:
o1 = (b + tmp)
branch4:
o1 = (a + tmp)
and we can form a table, 1s means the branch has such inputs, zero means hasn't.
| a | b | f | tmp | |
|---|---|---|---|---|
| branch1 | 1 | 1 | 0 | 0 |
| branch2 | 1 | 0 | 1 | 0 |
| branch3 | 0 | 1 | 0 | 1 |
| branch4 | 1 | 0 | 0 | 1 |
Then use the table to form a matrix:
$$
A=\begin{bmatrix}
1 & 1 & 0 & 0 \
1 & 0 & 1 & 0 \
0 & 1 & 0 & 1 \
1 & 0 & 0 & 1
\end{bmatrix}
$$
And the problem becomes:
$$
\begin{align}
(1)&Define\ a\ matrix\ A\ with\ m\ rows\ n\ columns\ ,a\ constant\ number\ c. \
&m\ equals\ to\ the\ number\ of\ branches,n\ equals\ to\ the\ number\ of\ inputs, c\ equals\ to\ the\ number\ of\ plus\ operators.\
&Therefore\ the\ elements\ in\ A\ can\ only\ be\ 0\ or\ 1,the\ number\ of\ 1s\ equal\ to\ c\ times\ m.\
&Apparently, if\ we\ add\ up\ all\ columns,we'll\ get \begin{bmatrix}c\c\c\c\\end{bmatrix}.\
(2)&Define\ \vec{i}\ as\ a\ representation\ of\ the\ i\ th\ column\ vector\ of\ matrix\ A.\
Problem:&Use\ as\ little\ as\ possible\ 'vector\ plus'\ operation\ and\ all\ columns\ to\ get\ c\ \begin{bmatrix}1\1\...\1\end{bmatrix}.\
Example:&A=\begin{bmatrix}
1 & 1 & 0 & 0 \
1 & 0 & 1 & 0 \
0 & 1 & 0 & 1 \
1 & 0 & 0 & 1
\end{bmatrix}\\
&\vec{1}+\vec{2}=\begin{bmatrix}1\1\1\1\\end{bmatrix},and\ A\ become\ A_1=
\begin{bmatrix}
1 & 0 & 0 \
0 & 1 & 0 \
0 & 0 & 1 \
0 & 0 & 1
\end{bmatrix}
\\
&\vec{2}+\vec{3}+\vec{4}=\begin{bmatrix}1\1\1\1\\end{bmatrix},and\ we\ get\ two\ (c = 2)\ \begin{bmatrix}1\1\1\1\end{bmatrix}\\
&so,the\ result\ is\ 3\ times\ of\ vector\ plus \ operation.
\end{align}
$$
So
In last part, we convert the problem into a math problem. But one thing need to be pay attention to, that is our algorithm need to be global optimum rather than local optimum. This means we can't use greedy strategy, which lead to the simulation of more consequences. Take the former case as an example. We can't claim that
We define the process of choosing two columns to do vector plus as an 'operation'. As far as you can see, for a 4*4 matrix, if we randomly choose two columns to do 'operation',it may cost at most m=4 times of 'operations' to get a [1,1,1,1] vector. So we can roughly calculate the scale of all consequences: $$ m \times C_n^2 \times c=O(mn^2c) $$. This complexity isn't durable. So we need to use some methods to decrease it.
First, this problem can form
The worst case is just similar to the Monte Carlo Method. We need to enumerate all situation to find the best consequence.