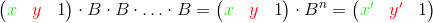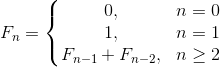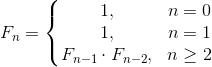cpmoptimize

Decorator for automatic algorithms optimization via fast matrix exponentiation

Installation

You can install the latest version of the library using pip:

sudo pip install git+https://github.com/borzunov/cpmoptimize.git

Or install previously downloaded and extracted package:

sudo python setup.py install

Dependencies (byteplay >= 0.2) will be installed automatically.

Basic Example

Let we want to calculate ten millionth Fibonacci number in Python. The function with trivial algorithm is rather slow:

def fib(n):
    a = 0
    b = 1
    for i in xrange(n):
        a, b = b, a + b
    return a

print fib(10 ** 7)

# Time: 25 min 31 sec

But if we use the described decorator the function will be able to figure out the answer much faster:

from cpmoptimize import cpmoptimize

@cpmoptimize()
def fib(n):
    a = 0
    b = 1
    for i in xrange(n):
        a, b = b, a + b
    return a

print fib(10 ** 7)

# Time: 18 sec (85x faster)

Explanation

Actually the decorator disassembles and analyzes function's bytecode and tries to optimize applied algorithm and reduce its complexity.

Disassembling bytecode performs using pretty byteplay library. This is the reason that the project is written in Python 2 branch.

The decorator uses the method implemented by Alexander Skidanov in his experimental simple optimizing interpreter.

This interpreter supports the following operations with numeric variables:

# Assign another variable or a constant
x = y
x = 2

# Add or subtract another variable or a constant
x += y
x += 2
x -= y
x -= 3

# Multiply by a constant
x *= 4

# Run a loop with a constant number of iterations
loop 100000
    ...
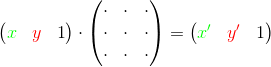
end

The interpreter can represent every supported operation as a special square matrix. To perform the operation is necessary to multiply a vector with old variables' values by this matrix and obtain a vector with new values:

To perform a sequence of the operations is necessary to multiply vector by all corresponding matrices. Another method is to multiply matrices first and then multiply source vector by the resulting product (using associativity of matrix multiplication):

To perform the loop we should compute a number n (number of loop's iterations) and a matrix B (product of the corresponding matrices in the loop's body). Then we should multiply source vector by B for n times. Another method is to construct the n-th power of the matrix B and then multiply source vector to the result:

To speed up these operations and reduce their complexity we can use the algorithm of exponentiation by squaring.

If the loop isn't operates with big numbers and arbitrary-precision arithmetic, it allows to change loop's complexity from O(n) to O(log n). In this case we can execute a loops with 10 ** 1000 iterations less than one second:

from cpmoptimize import cpmoptimize, xrange

@cpmoptimize()
def f(n):
    step1 = 1
    step2 = 1
    res = 1
    for i in xrange(n):
        res += step2
        step2 += step1
        step1 += 1
    return res

print f(10 ** 1000)

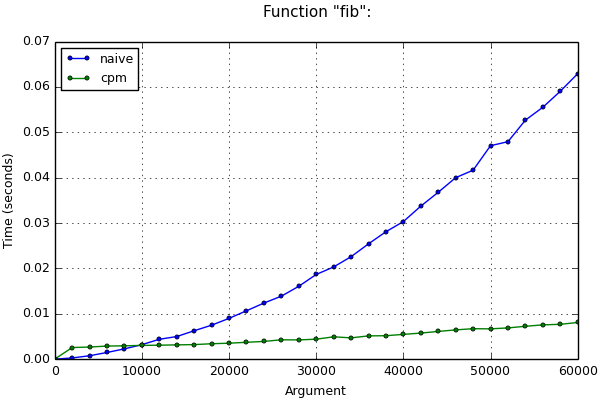
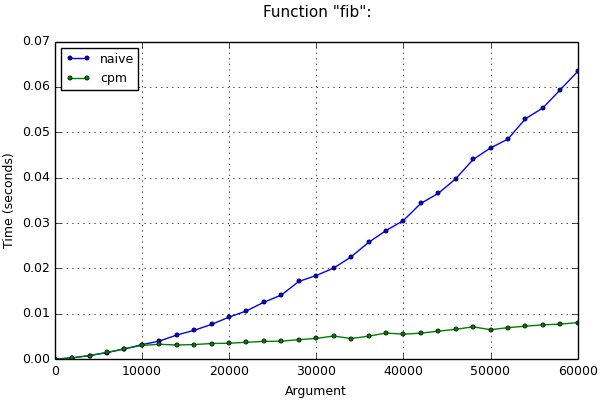
# Time: 445 ms

Even if loop operates with big numbers (as in the example with the Fibonacci numbers above), complexity is also reduced (but not so much). This can be seen in the following chart:

Application

When decades ago a programmer needed to multiply a variable by 4, he didn't use built-in multiplication operator, instead he used its faster equivalent - bit shifting to the left by 2. Nowadays compilers are able to apply such optimizations themselves. In the need of reducing development time new highly abstract languages, new convenient technologies and libraries were developed. Programmers spend more and more time telling computers what to do (multiply a variable by 4), not how to do it efficiently (use the bit shift). So now creating efficient code is partially the task of compilers and interpreters.

Currently compilers are able to replace the various operations to the more efficient ones, to predict expressions' values, to delete or swap some parts of the code. But they still can't replace the computation algorithm, written by programmer, to the new one with better complexity.

I tried to implement this idea in the described library. If you use it, it's enough to add a single line with the decorator before the function you want to speed up. The decorator optimizes loops if it's possible and never breaks the program, so it can be applied in real projects.

Let's look at one example. There is fast but nontrivial algorithm for calculating Fibonacci numbers, based on the same idea of computing the power of a matrices (you can see its implementation in the sample at "tests/fib.py"). An experienced programmer can implement this algorithm in a few minutes. If he don't need to perform the calculations quickly, most likely, he would prefer to save his working time and write a naive and slow algorithm.

Otherwise, if the calculations must work quickly, the programmer has two ways: to write the complex algorithm or to use the automatic optimization (apply the decorator). If n is sufficiently large, performance of the program will be similar in both cases, but the programmer will spend less working time in the second case.

In practice, you can also meet the following situation. If the sequence isn't given by known recurrent formula:

But given by more complicated formula, e.g.:

Then you can't google the corresponding fast algorithm and you should spend some efforts to make it. Nevertheless, you can write naive solution and apply the decorator, then the computer will build a fast algorithm for you itself:

from cpmoptimize import cpmoptimize

@cpmoptimize()
def f(n):
    prev3 = 0
    prev2 = 1
    prev1 = 1
    for i in xrange(3, n + 3):
        cur = 7 * (2 * prev1 + 3 * prev2) + 4 * prev3 + 5 * i + 6
        prev3, prev2, prev1 = prev2, prev1, cur
    return prev3

More Examples

You can see the comparison of the execution time with other algorithms for computing Fibonacci numbers and learn more benchmarks in "tests/" directory in the project sources. If matplotlib is installed on your system, you can also make the corresponding plots (they will be saved to "tests/plots" directory).

Library Interface

Library name comes from the words "compute the power of a matrix and optimize". It contains two elements.

Reimplemented xrange

cpmoptimize.xrange(stop)

cpmoptimize.xrange(start, stop[, step])

Built-in xrange in Python 2 doesn't support long integers as their arguments (passing them leads to OverflowError).

Since the library can run loops with 10 ** 1000 and more iterations in a short time, it provides its own implementation of xrange. This implementation supports all features of original xrange and moreover arguments with type long.

However, if in your case the number of iterations in the loops is small, you can continue to use built-in xrange.

Function cpmoptimize

cpmoptimize.cpmoptimize(strict=False, iters_limit=5000, types=(int, long), opt_min_rows=True, opt_clear_stack=True, verbose=None)

Applying the decorator

cpmoptimize function accepts optimization settings and returns the decorator that consider these settings. You can apply this decorator with special syntax with "@" symbol or without it:

from cpmoptimize import cpmoptimize

@cpmoptimize()
def f(n):
    # Code

def naive_g(n):
    # Code

smart_g = cpmoptimize()(naive_g)

Before modifying function's bytecode will be copied. Thus in code above only f and smart_g functions will be optimized.

Search for loops

The decorator look for normal for loops in function's bytecode. while loops, generator expressions and list comprehensions are ignored. Nested loops are not supported yet (only innermost loop is optimized). Constructions for-else are handled correctly.

Allowed types

Complex types can have user-defined side effects on application different operators. Changing the order of application of these operators can disrupt the proper program's behavior.

Further, during operations with matrices variables are added and multiplied implicitly, so the types of variables are shuffling. If one of the constants or variables have type float, the variables that would have type int after the code could also get the type float (since the addition of int and float returns float). This behavior can cause errors and is also unacceptable.

For these reasons, decorator optimizes loops only if all the variables and constants in them have one of an allowed types. By default only int and long types and their heirs are allowed (shuffling of these types usually does not cause undesirable effects).

To change set of allowed types, you should place a tuple of the relevant types to the types argument. Types from this tuple and their heirs will be considered as allowed (it will be checked by calling isinstance(value, types)).

Loop optimization conditions

Every found loop must satisfy a number of conditions. Some of them are checked at the stage of application of the decorator (during the bytecode analysis):

1. Loop's body must contain only assignment instructions and unary and binary operations, which may be arranged in a complex expressions. It can't contain conditions, function calls, return and yield operators etc.

2. Operands must satisfy the predictability conditions (their value must be the same at each iteration and mustn't depend on result of any computations in the previous iteration):

   • All operands of addition and subtraction and operand of the unary minus can be unpredictable.

   • At least one operand of multiplication must be predictable (similarly that only multiplication by a constant is allowed in the original interpreter).

   • All operands of exponentiation, division, taking the remainder and bitwise operations must be predictable.

3. All constant used in the loop must have allowed type.

If these conditions are satisfied, a special hook is installed to bytecode before the loop (the loop's original bytecode isn't removed). This hook will check the remaining conditions, which can be checked only immediately before the start of the loop due the dynamic typing in Python:

1. The object that the loop iterates must have built-in type xrange or its reimplementation cpmoptimize.xrange. Slow range function isn't supported.

2. Values of all variables used in the loop must have allowed type.

If the hook has concluded that optimization is admissible, the corresponding matrices will be calculated, and then values of used variables will change to the new ones. Otherwise the loop's original bytecode will be executed.

Loop-invariant code motion

Despite the fact that the described method doesn't support exponentiation and bitwise operations, the following code will be optimized:

@cpmoptimize()
def f(n, k):
    res = 0
    for i in xrange(n):
        m = 3
        res += ((k ** m) & 676) + i
    return res

When analyzing the bytecode the decorator concludes that the values of variables k and m in the expression (k ** m) & 676 don't depend on which iteration of the loop they are used, therefore the value of the whole expression doesn't change. It's enough to compute this value once moving relevant instructions and executing them immediately before the start of the loop. The source code will be converted to a code similar to the following:

@cpmoptimize()
def f(n, k):
    res = 0
    m = 3
    _const1 = (k ** m) & 676
    for i in xrange(n):
        res += _const1 + i
    return res

It's important that the invariant values are calculated every time on calling function because they can depend on global variables and function's parameters (for example, _const1 depends on parameter k). Now it's easy to optimize the resulting code via operations with a matrices.

The aforesaid checking of values predictability is perfomed at the same time. For example, if one of operands of bitwise AND have been unpredictable, this operation can no longer be taken out of the loop and optimization could not be applied.

Also the decorator partially supports multiple assignments. If they contains a few elements, Python generate supported bytecode without using tuples:

a, b = b, a + b

Parameter iters_limit

An optimized loop may run slower on a small number of iterations (it can be seen at the chart above) because it requires some time to construct the matrices and check the types. You can set the iters_limit parameter to neutralize this effect. Then hook will check number of the iterations in the loop before executing optimization and will cancel optimization if this number doesn't exceed the given parameter.

The limit is set to 5000 by default. It can't be set lesser than 2 iterations.

It's clear that the best value of the parameter is the point of intersection of the lines on the chart corresponding to the execution time of the original and optimized variants of the function. Then the function can choose the fastest algorithm in each case:

Flag strict

Sometimes it's necessary to apply the optimization. For example, program will hang if a loop with 10 ** 1000 iterations will not be optimized. Flag strict is created for such cases. It's disabled by default, but if you enable it, program will throw exception if one of normal for loops will not be optimized.

If the optimization fails at the stage of application the decorator, cpmoptimize.recompiler.RecompilationError will be raised. For example, let's try to multiply two unpredictable variables:

>>> from cpmoptimize import cpmoptimize
>>>
>>> @cpmoptimize(strict=True)
... def f(n, k):
...     res = 0
...     for i in xrange(n):
...         res += i * res
...     return res
... 
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
  File "cpmoptimize/__init__.py", line 100, in upgrade_func
    index += analyze_loop(settings, code, index) + 1
  File "cpmoptimize/__init__.py", line 59, in analyze_loop
    raise err
cpmoptimize.recompiler.RecompileError: Multiplication of two unpredictable values is unsupported

If the optimization fails during the checks in the hook (it was found that the iterator or variables types aren't supported), TypeError will be raised:

>>> from cpmoptimize import cpmoptimize
>>>
>>> @cpmoptimize(strict=True)
... def f(iterable):
...     res = 0
...     for elem in iterable:
...         res += elem
...     return res
... 
>>> f(xrange(30))
435
>>> f(range(30))
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
  File "<stdin>", line 4, in f
  File "cpmoptimize/hook.py", line 170, in exec_loop
    raise err
TypeError: Iterator in optimized loops must have type "xrange" instead of <type 'list'>

Options of advanced optimization

Flags opt_min_rows and opt_clear_stack are responsible for using additional methods of optimizing during constructing of the matrices. They are enabled by default and can be disabled only for demonstration purposes.

Usually the multiplication of long numbers in some cells of generated matrices takes most of the execution time of the optimized code. Multiplication of the other cells is negligible in comparison with this time-consuming process.

During recompilation the decorator creates temporary, virtual variables corresponding to the positions of the Python's interpreter stack. After complex computations they can contain long numbers that already saved in another, real variables. Actually we don't need to save these values and multiply they again during matrices multiplication. Option opt_clear_stack enables mechanism of clearing these variables: if we assign them to zero at the end of their use, long values therein will disappear.

This option is particularly effective when program operates with very big numbers. Excluding of excess multiplications can speed up the program more than two times.

Option opt_min_rows activates algorithm of reducing size of the used square matrices. Unnecessary rows and columns corresponding to unused and predictable variables will be excluded.

This option can speed up the program on a small number of the iterations, when the numbers were not very big yet and the dimensions of the matrix are important for execution time.

If you use both options at the same time, virtual variables begin to have predictable value (zero) and opt_min_rows works more efficiently. Therefore effectiveness of both options together is greater than effectiveness of each option separately.

The following chart shows the execution time for computing Fibonacci numbers during disabling different options ("-m" means that opt_min_rows is disabled, "-c" means that opt_clear_stack is disabled, "-mc" means that both options are disabled):

Parameter verbose

Option verbose allows you to collect more information about failed and successful optimizations to profile your program and find reasons for which optimizations weren't applied. The parameter is set to None by default. To enable the option you should assign to the parameter a stream that will be used for writing debug messages (for example, sys.stderr).

Why Python?

During developing the library I used the fact that you can analyze and modify the bytecode generated by Python interpreter at run-time without modifying the interpreter. Actually it gives great opportunities for extending the language and the interpreter. Also, the advantages of the described method particularly occurs during use arbitrary-precision arithmetic, which is built in Python.

Therefore, implementation of the described optimization in Python has become a more interesting problem for me, although, of course, its application in C++ compilers would create more fast programs. Nevertheless, the optimized by the decorator Python code outperforms naive C++ code due to better algorithm complexity.

What's next?

Changing the set of operations

Let's say that our method supports a pair of operations 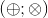if it's possible to:

• Apply operation to two variables or to a variable and a constant;

• Apply operation to a variable and a constant.

We already know that our method supports the pair of operations because it's possible to:

• Add two variables or a variable and a constant;

• Multiply a variable by a constant.

Exactly these operations are implemented in the decorator now. But it turns out that described method supports another pairs of operations, e.g. (pair of multiplication and exponentiation).

For example, we can try to find n-th number in the sequence given by the following recurrent formula:

If the decorator supports the pair , we could multiply a variable by another variable (but couldn't add variables). Then naive solution for described problem could be accelerated by the decorator:

def f(n):
    a = 1
    b = 1
    for i in xrange(n):
        a, b = b, a * b
    return a

To implement the pair we could operate not with variables' values, but with logarithms of these values. Then multiplication will be replaced by addition of this logarithms and constructing of a constant power will be replaced by multiplying a number by the constant. It reduces the problem to the considered case with the pair .

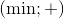
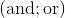
It's possible to proof that the method also supports pairs , and (where and is bitwise AND and or is bitwise OR) because the associativity of matrix multiplication or similar properties are maintained in this cases.

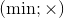
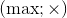
In case of positive numbers it's also possible to work with pairs and .

Nested loops

We can modify algorithm that analyzes loops in the bytecode to support a code like this:

def f():
    res = 0
    for i in xrange(10 ** 50):
        for j in xrange(10 ** 100):
            res += i * 2 + j
    return res

Predictable conditions

The condition in the loop at the following code is predictable. We can find out its truth before starting of the loop and remove non-executed branch of the code. The resulting code can be optimized:

def f(mode):
    res = 0
    for i in xrange(10 ** 50):
        if mode == 1:
            res += 3
        else:
            res += 5
    return res

Author

Copyright (c) 2014 Alexander Borzunov

A detailed article and discussion in Russian: http://habrahabr.ru/post/236689/