CBIR

• Javier Gil Domínguez
• Jorge Saénz de Miera Marzo
• Pablo Martín Escobar
• Nicolás Vega Muñoz

Como usar

Es tan sencillo como ejecutar el archivo 'CBIR_gui.py'. Posteriormente tan solo deberas elegir la imagen de consulta y el algoritmo deseado.

Índice

Introducción

Metodología

Histogramas

Harris

ORB

SIFT

CNN

CNN + SIFT

Interfaz Gráfica

Conclusiones

Referencias

INTRODUCCIÓN

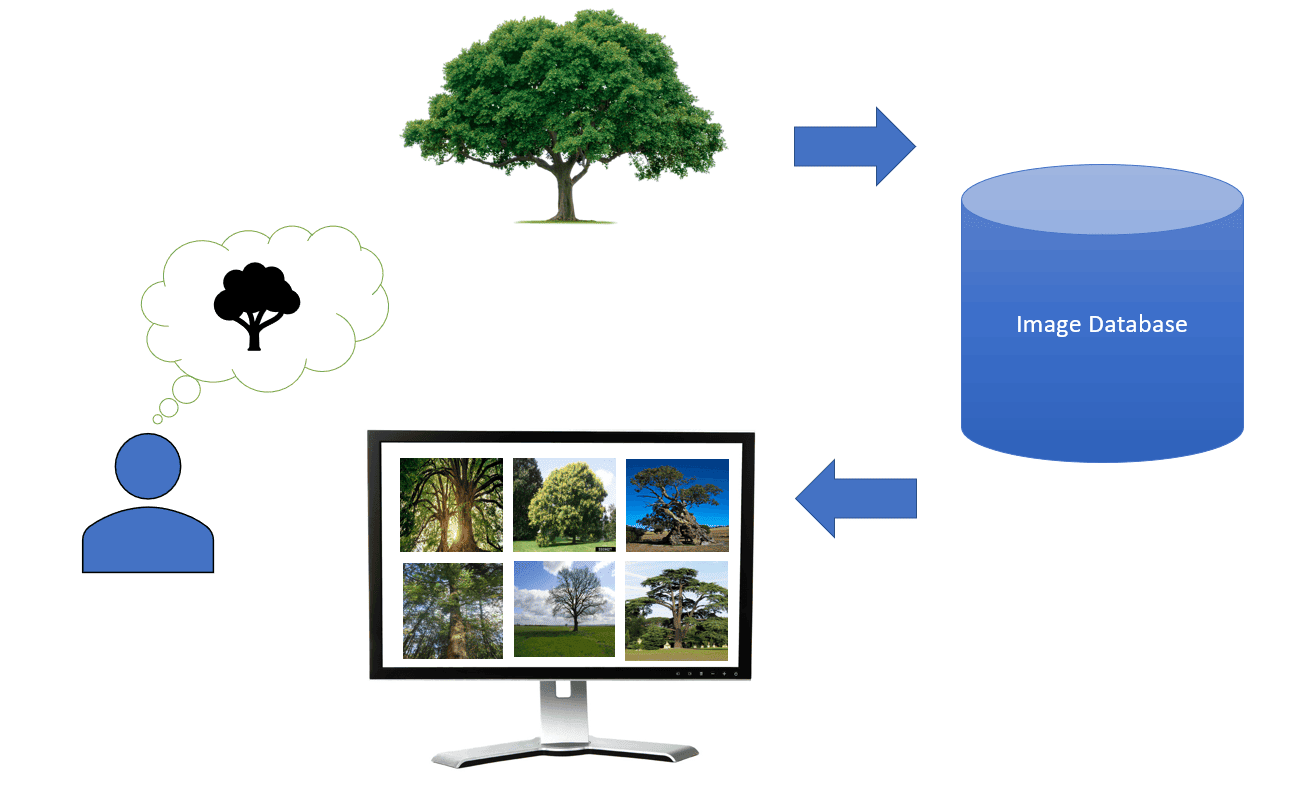
El CBIR (Content-Based Image Retrieval) es un tipo de búsqueda de imágenes que utiliza el contenido de ellas para recuperar otras similares. Esto significa que, a diferencia de la búsqueda de imágenes basada en etiquetas, el CBIR no requiere que las imágenes estén etiquetadas con palabras clave o metadatos para que se puedan recuperar.

El CBIR funciona extrayendo características de las imágenes. Estas características pueden ser de naturaleza visual, como el color, la textura o la forma, o de naturaleza semántica, como el contenido de la imagen. Una vez que se han extraído las características, se pueden utilizar para comparar las imágenes y recuperar las que son más similares.

Hemos implementado dos enfoques principales para el diseño de un sistema CBIR:

• Basados en características locales (Harris, Fast, SIFT...)

• Basados en características globales (histogramas de color/texturas, CNN.)

El CBIR es una tecnología en constante evolución. A medida que las técnicas de extracción de características y comparación de imágenes mejoran, el CBIR se vuelve más preciso y eficiente.

Realizaremos distintas implementaciones del sistema CBIR y evaluaremos los resultados para cada una de ellas. Las distintas implementaciones serán:

• Histograma de color
• Histograma de texturas
• Harris
• ORB
• SIFT
• CNN
• CNN + SIFT

METODOLOGÍA

Para la evaluación de cada implementación definimos las siguientes métricas:

• Precision: Mide la proporción de imágenes recuperadas que son relevantes.

Precision = (Imágenes relevantes recuperadas) / (Número total de imágenes recuperadas)

• Recall: Mide la proporción de imágenes relevantes que han sido recuperadas

Recall = (Imágenes relevantes recuperadas) / (Número total de imágenes relevantes)

El número total de imágenes relevantes lo establecemos a 100 debido a que tenemos 100 imágenes de cada categoría. Aún así es posible que se dé el caso de una imagen, por ejemplo un coche concreto perteneciente a la categoría 'coches', y haya a la vez una imagen que contenga ese mismo coche en una imagen de la categoría 'ciudad'. Bajo nuestro punto de vista ésta imagen también sería relevante pese a no pertenecer exactamente a la categoría 'coche', pero ante la imposibilidad de supervisar manualmente todas las posibles imágenes relevantes optamos por fijar a 100 este valor.

Para evaluar los sistemas CBIR observaremos los valores de ambas métricas, así como el tiempo de ejecución medio, pues deseamos mantener un equilibrio entre resultados y recursos computacionales. Para cada sistema CBIR realizaremos 10 consultas y obtendremos la media de los valores de precision y recall para obtener unos valores más acordes a la realidad, ya que hemos comprobado experimentalmente que hay categorías que funcionan mejor con ciertos modelos que con otros.

Usaremos siempre las mismas 10 imágenes para evaluar cada sistema CBIR. Esta elección se basa en nuestra observación de que ciertas clases tienden a ser más frecuentes en algunas implementaciones. El objetivo es evitar que un sistema CBIR obtenga una precisión sesgada, ya sea más baja o más alta, debido a la presencia variable de imágenes que podrían favorecer o perjudicar el rendimiento del modelo.

Las imágenes de evaluación han sido obtenidas seleccionando aleatoriamente 10 categorías distintas, y posteriormente obteniendo una imagen aleatoria de cada categoría.

Éstas son:

Perro Mono Coche IPod Autobús Puente Helado Plátano Pizza Mar

DATASET

El dataset usado para entrenar y evaluar nuestros sistemas CBIR es un subconjunto de ImageNet. Este dataset consiste de 14 millones de imágenes de resolución 64x64 etiquetadas en más de 1000 clases distintas. Nuestro problema no consiste en la clasificación, por lo que podemos descartar las etiquetas para entrenar el modelo.

Hemos obtenido un subconjunto de este debido a la gran cantidad de imágenes y espacio de almacenamiento que requiere este dataset. Hemos muestreado manualmente las imágenes del dataset original, seleccionando 20 clases aleatoriamente y cogiendo de cada clase las 100 primeras imágenes, obteniendo así un total de 2000 imágenes para entrenar los modelos.

Las clases seleccionadas aleatoriamente son:

• Autobús
• Clavos
• Coche
• Collarín
• Desatascador
• Gatos
• Mono
• Puente
• Silla
• Perro
• Pato
• Pizza
• Mar
• iPod
• Plátano
• Máscara de gas
• Pajarita
• Mosca
• Helado
• Cañón

HISTOGRAMAS

Nuestra primera implementacion, y la más sencilla, se basa en los histogramas de color y de texturas. Son técnicas similares pero con una diferencia de enfoque inicial. Estas son las principales características:

HISTOGRAMAS DE COLOR :

• Representación de la información cromática : Los histogramas de color se centran en la distribución de colores en una imagen. Ayudan a describir la apariencia de la imagen en términos de sus componentes de color (por ejemplo, rojo, verde y azul en el modelo RGB).

• Invariante a la textura : Los histogramas de color no capturan información sobre la textura de una imagen. Dos imágenes con los mismos colores pero diferentes texturas pueden tener histogramas de color similares.

HISTOGRAMAS DE TEXTURAS :

• Representación de patrones repetitivos : Los histogramas de texturas se utilizan para capturar patrones repetitivos o texturas en una imagen. Estos patrones pueden ser pequeñas estructuras repetitivas (como patrones de puntos) o características más grandes y complejas.

• Basados en la distribución de niveles de gris : Los histogramas de texturas generalmente se crean a partir de los niveles de gris de una imagen. Pueden describir cómo los niveles de gris están distribuidos en una imagen y cómo los patrones de textura se manifiestan en esta distribución.

• Sensible a la textura : A diferencia de los histogramas de color, los histogramas de texturas están diseñados específicamente para capturar información sobre la textura de una imagen. Por lo tanto, dos imágenes con la misma distribución de colores pero con texturas diferentes tendrán histogramas de texturas distintos.

En ambos casos, la evaluación de los modelos es subjetiva ya que, en el caso de los histogramas de color por ejemplo, puede funcionar bien si muestra imágenes con los mismos colores que la imagen de entrada pero puede que estas imágenes no se parezcan en nada en cuanto a contenido, por lo que en este apartado, no vamos a medir el rendimiento del modelo a partir de precision y recall.

Antes de evaluar el modelo nuestra hipótesis es que no vamos a obtener buenos resultados. Nos basamos en que desde ésta aproximación no estamos teniendo en cuenta en ningún momento el contenido de la imagen, que es en lo que se basa un sistema de recuperación de contenido. Las imágenes que recuperemos tendrán una distribucion de color similar, pero el contenido de las mismas no tendrá por que serlo.

Ejemplo consulta histograma de color:

Vemos que, como hemos supuesto antes, respecto al color sí que es una buena solución ya que los colores son más o menos constantes durante todas las imágenes, aunque esto no ocurre igual para el contenido.

Otro ejemplo de consulta histograma de color:

Vemos que pueden darse casos en los que coincidan tanto color como contenido por lo que estas serían las mejores soluciones usando los histogramas de color.

Ejemplo ejecución histograma de texturas:

Procedemos a evaluar el CBIR implementado el Histograma de Color :

Ejecucion	Precision	Recall	Tiempo ejec (s)
1	0.2	0.02	0.03
2	0.2	0.02	0.03
3	0.1	0.01	0.02
4	0.1	0.01	0.02
5	0	0	0.03
6	0.2	0.02	0.02
7	0.1	0.01	0.02
8	0	0	0.02
9	0.9	0.09	0.02
10	0.3	0.03	0.03
AVG	0.21	0.021	0,123

Y ahora procedemos a evaluar el CBIR implementado el Histograma de textura:

Ejecucion	Precision	Recall	Tiempo ejec (s)
1	0.3	0.03	0,06
2	0	0	0,07
3	0.1	0.01	0,08
4	0	0	0,05
5	0.1	0.01	0,05
6	0.1	0.01	0,06
7	0	0	0,06
8	0	0	0,06
9	0.5	0.05	0,07
10	0	0	0,06
AVG	0.11	0.011	0,062

Como conclusión, podemos decir que este tipo de soluciones (realizadas mediante histogramas), si bien pueden tener un enfoque inicial distinto en el que el contenido de la imagen no es lo principal a detectar sino que lo son otros áreas, como puede ser el área cromática, no es la mejor solución que estamos buscando ya que nuestro objetivo principal es describir el contenido de cada imagen.

HARRIS

Este método se basa en la detección de cambios abruptos en la intensidad de píxeles en diferentes direcciones, lo que indica la presencia de una esquina. El propósito principal de Harris Corner Detection es identificar puntos de interés (esquinas) que son invariantes a la rotación, cambio de escala y cambios en la iluminación.

Pasos que realiza el algoritmo :

• Aplicar un operador de Sobel para buscar los valores de gradiente en 'x' y en 'y' para cada píxel en la imagen en tonos grises.
• Para cada píxel 'p' en la imagen en tonos de grises, considerar una ventana de 3x3 alrededor de cada píxel que calculo la función de intensidad.
• Encontrar todos los píxeles que excedan un cierto valor de umbral y sean los máximos locales dentro de una cierta ventana (para prevenir detectar más de una vez la característica).

La principal ventaja de este algoritmo es la rapidez con la que se calcula y la sencillez a la hora de entender y aplicar esta técnica. Sin embargo, la precisión con la que reconoce el contenido no es la ideal ya que tenemos que tener en cuenta que el algoritmo Harris no está específicamente diseñado para la comparación de similitud entre dos imágenes, sino más bien para la detección de esquinas en imágenes. Por lo tanto, no es la mejor opción para comparar la similitud global entre dos imágenes.

Procedemos a evaluar el CBIR implementado HARRIS:

Ejecucion	Precision	Recall	Tiempo ejec (s)
1	0.1	0.01	4.61
2	0.1	0.01	1.57
3	0	0	2.47
4	0.1	0.01	2.14
5	0	0	1.72
6	0	0	2.07
7	0	0	2.36
8	0.1	0.01	3.89
9	0.1	0.1	2.57
10	0.1	0.01	2.23
AVG	0.06	0.006	2,58

Ejemplo ejecución:

ORB

El algoritmo ORB (Oriented FAST and Rotated BRIEF) es una alternativa eficiente a SIFT y SURF, que son algoritmos patentados. ORB es capaz de detectar características de manera efectiva y es mucho más rápido que SURF y SIFT.

Las contribuciones principales de ORB son las siguientes:

• Agregó una componente de orientación rápida y precisa a la detección de puntos clave FAST.
• Calcula eficientemente características BRIEF orientadas.
• Analiza la varianza y la correlación de las características BRIEF orientadas.

Implementa un método de aprendizaje para descorrelacionar características BRIEF bajo la invariancia rotacional, lo que mejora el rendimiento en aplicaciones de búsqueda de vecinos más cercanos.

Para describir los puntos clave, ORB utiliza BRIEF (Binary Robust Independent Elementary Features), que convierte los puntos clave en vectores binarios. Cada punto clave se describe mediante un vector de características binarias de 128 a 512 bits.

Otra característica de gran importancia, es que a la hora de la implementación de este algoritmo se puede elegir el tipo de puntuación utilizado para clasificar las características. Puede ser HARRIS_SCORE (utiliza el algoritmo Harris) o FAST_SCORE (un poco más rápido pero produce características ligeramente menos estables).

Vamos a implementar ORB, pero es bastante parecido en cuanto a sus virtudes y defectos, al algoritmo Harris. Estamos hablando de un algoritmo que nos permite obtener de forma rápida características y es fácilmente manejable, sin embargo en cuanto a rendimiento es bastante mejorable en cuanto a precisión hablamos.

No obstante, podemos ver como su precisión es mejor que el del detector de caracteristicas anteriores.Puede no ser tan robusto en comparación con algoritmos más avanzados como SIFT o SURF en ciertos escenarios, pero es una opción sólida para aplicaciones en las que la velocidad y la eficiencia son consideraciones clave.

Ejecucion	Precision	Recall	Tiempo ejec (s)
1	0.1	0.01	6.45
2	0	0	5.07
3	0.4	0.04	6.75
4	0.1	0.01	3.10
5	0.1	0.01	3.81
6	0.7	0.07	2.88
7	0	0	4.20
8	0	0	2.80
9	0.2	0.02	7.22
10	0.3	0.3	1.66
AVG	0.19	0.019	4.39

Ejemplo ejecución:

SIFT

Ahora haremos uso de los descriptores SIFT de una imagen para hallar imágenes similares.

Los descriptores SIFT (Scale-Invariant Feature Transform) son representaciones numéricas que se utilizan para describir las características clave o puntos de interés en una imagen. Estos descriptores son invariantes a cambios de escala, rotación, iluminación y perspectiva, lo que los hace útiles en tareas de reconocimiento de objetos y coincidencia de imágenes. Cada descriptor SIFT se calcula en función de la información de los píxeles en una región alrededor de un punto clave detectado en la imagen, y se utiliza para identificar y comparar características visuales en imágenes.

Un vector SIFT es un vector de características locales consistente de 128 valores. Cada imagen tiene un número variable de descriptores SIFT. Al tratarse de un vector de características locales no podemos encontrar imágenes similares a partir de un único descriptor, por lo que tendremos que encontrar los descriptores más similares de cada descriptor de nuestra imagen de consulta. Hemos realizado distintas implementaciones de este.

• Basado en distancias
• Basado en cuentas
• Basado en matching

Todas éstas implementaciones tienen un procedimiento similar. La medida de distancia entre descriptores será la euclídea. Haremos usó de KNN para obtener las distancias y los n vecinos más cercanos de un descriptor dado, para posteriormente obtener la distancia media o contar las apariciones de cada imagen como imagen cercana.

Basado en distancias

Nuestra primera implementación se basa en usar la media de las distancias de cada descriptor de la imagen de consulta a los descriptores de otra imagen para medir la similitud entre éstas.

El procedimiento es el siguiente:

1. Obtenemos todos los descriptores de la imagen de consulta.
2. Calculamos la distancia euclídea de cada descriptor de la imagen de consulta a todo el resto de descriptores, obteniendo los ID de las imágenes a los que pertenecen y almacenando las distancias entre estos descriptores. De ésta forma almacenamos para cada imagen la suma de todas las distancias que ha habido con cada descriptor.
3. Calculamos la media de las distancias a cada imagen.
4. Ordenamos las imágenes de menor a mayor distancia.

El principal inconveniente de esta implementación es que permite que una imagen con tan sólo 1 descriptor similar al de consulta aparezca como más similar que otra imagen con muchos descriptores similares con una distancia mayor. Este sería el caso extremo, pero de forma general se podría decir que imágenes con pocos descriptores tienen más posibilidades de aparecer como más cercanos.

Procedemos a evaluar el sistema CBIR:

Ejecucion	Precision	Recall	Tiempo ejec (s)
1	0	0	19.381
2	0.1	0.01	13.353
3	0	0	12.541
4	0	0	10.159
5	0	0	16.922
6	0.3	0.03	14.709
7	0	0	10.425
8	0	0	5.027
9	0.5	0.05	23.727
10	0.7	0.07	3.276
AVG	0.16	0.016	12.956

Obtenemos una precisión bastante baja, además de unos tiempos de ejecución sorprendentemente largos. No parece que esta sea una buena implementación.

Ejemplo de consulta:

Basado en cuentas

Ésta implementación es similar a la anterior, pero en vez de calcular la distancia de cada descriptor de consulta con todo el resto de descriptores tan sólo obtenemos los n descriptores más cercanos. Ésta vez no calcularemos la distancia entre los descriptores, sino que tan solo observaremos cuantas veces aparece un descriptor de una imagen como uno de los n más similares. Desde este punto de vista consideramos que 2 imágenes son más similares que otra si éstas tienen más descriptores comunes entre los n más cercanos, siendo n un número a elegir que recomendablemente adoptará un valor bajo pues en este enfoque no deseamos calcular todas las distancias entre todos los descriptores, sino obtener siempre descriptores de mínima distancia. El número de vecinos cercanos lo fijamos en 50 pues queremos que sea un número bajo ya que sólo queremos descriptores verdaderamente similares, este valor podría modificarse ligeramente sin experimentar grandes cambios.

La estrategia para determinar las imágenes más similares será la siguiente:

1. Obtenemos para cada descriptor de la imagen de consulta sus n descriptores más cercanos.
2. Obtenemos los ID de las imágenes a las que pertenecen dichos descriptores.
3. Contabilizamos las veces que aparece un descriptor de una imagen entre los 50 más cercanos.
4. Recuperamos las n imágenes con mayor número de apariciones.

El principal inconveniente de esta implementación sucede en el caso de que cada descriptor sea muy similar únicamente al descriptor de otra imagen. De ésta forma cada descriptor de la imagen de consulta sugiere que la imagen más similar es una distinta para cada descriptor, con el mismo número de ocurrencias para cada imagen.

Procedemos a evaluar el sistema CBIR:

Ejecucion	Precision	Recall	Tiempo ejec (s)
1	0.3	0.03	0.992
2	0	0	0.956
3	0.1	0.01	0.906
4	0.8	0.06	0.704
5	0.4	0.04	1.21
6	0.7	0.08	1.035
7	0.3	0.03	0.742
8	0	0	0.432
9	0.1	0.01	1.982
10	0.3	0.03	0.267
AVG	0.3	0.03	0.9226

Bajo este enfoque hemos logrado prácticamente aumentar la precisión del modelo al doble, manteniendo los tiempos de ejecución por debajo del segundo.

Ejemplo consulta:

Basado en matching

Hacemos usó de los descriptores SIFT con un enfoque distinto. En este caso haremos usó de BFMatcher para hallar imágenes similares. Para ello tan sólo nos es necesario obtener todos los descriptores de la imagen de consulta y hallar los matches. Una vez hallado queremos descartar aquellos matches que no sean de calidad, esto lo logramos mediante el usó del Lowe´s ratio, en nuestro caso será de 0.85. Esto quiere decir que si la distancia entre la mejor coincidencia es menor que el 85% de la distancia de la segunda mejor coincidencia , entonces se considera que esta coincidencia es de buena calidad y se guarda. El valor de 0.85 ha sido establecido por conveniencia, puesto que usando el predeterminado, 0.7, no se obtenían resultados.

A la hora de evaluar este sistema nos surge una complicación debido a que en este caso el número de imágenes similares que devuelve es un número variable, que depende de cuantas imágenes hayan superado el umbral fijado. Generalmente se devuelven pocas imágenes debido a este motivo.

Una vez tenemos nuestras 'buenas' coincidencias simplemente obtenemos los índices de las imágenes a las que corresponden y las consideramos como imágenes similares.

Procedemos a evaluar el modelo:

Ejecución	Precision	Recall	Tiempo ejec (s)
1	0	0	0.044
2	0	0	0.038
3	0	0	0.034
4	0	0	0.034
5	0.5	0.01	0.045
6	0.6	0.03	0.046
7	0	0	0.030
8	0	0	0.026
9	0	0	0.024
10	0	0	0.021
AVG	0.11	0.004	0.034

Como era de esperar no obtenemos unos buenos resultados.

Ejemplo de consulta:

CNN

Este es nuestro enfoque más optimista debido al aumento de complejidad del modelo y a la mejor eficacia que presentan las CNNs para entender semánticamente el contenido de la imagen.

Procedemos en ésta ocasión a trabajar con un descriptor de características globales en vez de uno de características locales. El vector lo obtendremos de una red convolucional preentrenada, concretamente la VGG16. El vector será el correspondiente a la última capa de la red convolucional, de longitud 25088 una vez aplanado.

Esta implementación es más sencilla que la anterior puesto que al tratarse de un vector de características globales es este directamente el que introduciremos en el modelo de KNN para obtener las imágenes más similares. Al igual que hemos hecho ya previamente en primer lugar calcularemos los vectores de características de todas las imágenes y los almacenaremos en una matriz numpy ('CNN_matrix.npy'), añadiendo 2 valores iniciales que corresponden a la carpeta e id de la imagen para posteriormente poder recuperarla.

Procedemos a evaluar el CBIR implementado con CNN:

Ejecucion	Precision	Recall	Tiempo ejec (s)
1	1	0.1	0.359
2	0.1	0.01	0.364
3	0	0	0.362
4	0.2	0.02	0.405
5	0.5	0.05	0.362
6	0.6	0.06	0.374
7	0.1	0.01	0.366
8	0.4	0.04	0.402
9	0.6	0.06	0.364
10	1	0.1	0.371
AVG	0.45	0.045	0.365

Como preveíamos este modelo nos brinda los mejores resultados hasta ahora, y en tiempos de ejecución mínimos. Obtenemos una precision de 0.45, lo que significa que el 45% de las imágenes que recuperemos serán relevantes. Se trata de un resultado bastante satisfactorio.

Ejemplo de ejecución:

CNN + SIFT

Los resultados anteriores ciertamente son mejores que la búsqueda aleatoria, pero aún así aspiramos a obtener mejores resultados. Por ello optamos por una implementación que combine los resultados de CNN y SIFT, las 2 implementaciones que mejores resultados nos han dado.

En ésta implementación estamos combinando un vector de características globales (CNN) con uno de características locales (SIFT). La implementación será análoga a la realizada en SIFT basado en cuentas, incorporando los 25088 valores de la CNN al vector.

El primer paso será normalizar los vectores de características por separado pues la magnitud de los valores tomados en ellos es distinta:

El resto es análogo a la implementación realizada con SIFT basado en cuentas.

La implementación de este sistema CBIR es complicada, o incluso imposible bajo los recursos computacionales de los que disponemos. Tan sólo calcular la matriz numpy que almacenará todos los descriptores requiere que se calcule por lotes y tras una larga ejecución logramos obtenrerla, ocupando unos 14 GB de almacenamiento. Esto sólo lo hemos logrado sin normalizar los datos de ambos, pues al tratar de normalizarlos obtenemos errores de RAM e incluso el reinicio automático de nuestra máquina debido a la falta de memoria (disponemos de 16GB de RAM en local y en Google Colab disponemos de 12 GB).

La evaluación es incluso más complicada, puesto que sólo funciona el modelo sin normalizar los datos, lo que teóricamente no es correcto, y experimentalmente vemos que obtenemos resultados muy similares a los obtenidos por CNN. Esto es debido a que la parte del vector correspondiente a CNN es mucho mayor que la correspondiente a SIFT (25088>>128). Es cierto que los valores SIFT sin normalizar son más grandes que los de CNN, pero no llega a ser compensado por lo anterior.

Por todo ello no podemos estar seguros de si ésta implementación es más adecuada que el resto, nuestra hipótesis es que sí lo sería, pero no tenemos forma de comprobarlo. Aún así habría que tener en cuenta cuánto mejora la precisión a costa de la notable carga computacional que ésta implementación conlleva y los gastos asociados.

INTERFAZ GRÁFICA

Para la interfaz gráfica hemos utilizado la librería Tkinter. Para desplegarla basta con ejecutar el archivo CBIR_gui.py y se nos abrirá una ventana en nuestro ordenador como esta:

Para utilizar la aplicación, debemos hacer click en el botón "Elegir imagen". Al darle, veremos que se nos abre el navegador de archivos del ordenador en una nueva ventana. Ahí deberemos elegir la imagen con la que queremos realizar la búsqueda.

Esta imagen puede ser cualquiera, pero debemos tener en cuenta que los algoritmos que utiliza la aplicación, se han entrenado con imágenes de un tamaño específico (32x32) y con imágenes pertenecientes a unas clases específicas, por lo que, al utilizar cualquier imagen que se salga de esto, seguramente no se obtengan buenos resultados. Por esto, recomendamos utilizar alguna de las imágenes que están en la carpeta dataset/test/ en el GitHub. Estas imágenes son del mismo tamaño que las utilizadas para entrenar a los algoritmos, y de las mismas clases.

Una vez seleccionemos la imagen para hacer la búsqueda, se abrirá en nuestra ventana, quedando así:

Lo siguiente que debemos hacer es seleccionar uno de los algoritmos que se proponen (CNN, SIFT, COLOR HISTOGRAM, HARRIS, ORB). Todos ellos utilizan el mismo código de los notebooks, que ya se han comentado. Hemos decidido poner estos, porque representan bien todas las pruebas realizadas, CNN es el que mejor funciona, de SIFT nos hemos quedado con la versión basándonos en cuentas, Color Histogram, devuelve las imágenes esperadas (aquellas con colores similares), y ORB que funciona razonablemente bien, y es bastante rápido

Además tenemos que elegir el número de imágenes que queremos como resultado con la scrollbar de abajo.

Con estos dos parámetros, y con la imagen abierta, nos quedaría la ventana de la siguiente forma:

Una vez seleccionados los parámetros, ya podemos hacer click en "Calcular imágenes". Esto ejecutará el algoritmo seleccionado con la imagen elegida, y mostrará el número de imágenes especificado que más se parece, dentro de nuestro dataset, quedando algo así:

CONCLUSIONES

Los resultados obtenidos no son perfectos, creemos que esto es debido a diferentes motivos:

• 'Pocos' datos de entrenamiento de cada categoría: 100 imágenes por categoría.
• Capacidad de cómputo limitada: incapacidad para normalizar en CNN+SIFT.
• Baja resolución de imágenes: 64x64, limitada por recursos computacionales.
• Falta de tiempo para aplicar un sistema más completo: ColorHist+CNN+SIFT por ejemplo.

Aún así creemos que hemos logrado unos resultados sorprendentemente buenos teniendo en cuenta los recursos y el tiempo disponible.

Inicialmente, sin sistema de recuperación de contenido alguno, la probabilidad de obtener una imagen similar dada una de consulta es la correspondiente a la búsqueda aleatoria:

nº imágenes relevantes / total imágenes = 100 / 2000 = 0.05

Esto es, dada una imagen de consulta, si seleccionamos una imagen aleatoriamente, la probabilidad de que ésta sea relevante es de un 5%.

Hemos evaluado nuestros modelos principalmente mediante la métrica 'precision', definida:

Precision = (Imágenes relevantes recuperadas) / (Número total de imágenes recuperadas)

Bajo ésta métrica, el modelo aleatorio evaluando sobre la recuperación de 10 imágenes aleatorias obtendrá una precisión también de 0.05.

Bajo nuestro sistema CBIR con mayor precisión, CNN, conseguimos aumentar la precisión de 0.05 a 0.45, y con unos tiempos de ejecución bastante buenos, tardando 0.365s de media en devolver 10 imágenes 'similares'.

Teniendo en cuenta estos resultados, consideramos que se ha llegado a un resultado verdaderamente competitivo teniendo en cuenta las limitaciones mencionadas.

REFERENCIAS

• CBIR research '2011 International Conference on Physics Science and Technology (ICPST 2011) Content-Based Image Retrieval Research'

https://www.sciencedirect.com/science/article/pii/S1875389211007279

• OpenCv Guideline

https://docs.opencv.org/3.4/index.html

• Solano, G. (2021, enero). GUI con Tkinter y OpenCV en Python | Imágenes ?️_: GUI usando Tkinter y OpenCV con Python._ Omes. https://omes-va.com/tkinter-opencv-imagen/
• Tkinter — Interface de Python para Tcl/Tk

https://docs.python.org/es/3/library/tkinter.html

25