给你一个二维字符网格数组 grid ,大小为 m x n ,你需要检查 grid 中是否存在 相同值 形成的环。
一个环是一条开始和结束于同一个格子的长度 大于等于 4 的路径。对于一个给定的格子,你可以移动到它上、下、左、右四个方向相邻的格子之一,可以移动的前提是这两个格子有 相同的值 。
同时,你也不能回到上一次移动时所在的格子。比方说,环 (1, 1) -> (1, 2) -> (1, 1) 是不合法的,因为从 (1, 2) 移动到 (1, 1) 回到了上一次移动时的格子。
如果 grid 中有相同值形成的环,请你返回 true ,否则返回 false 。
示例 1:
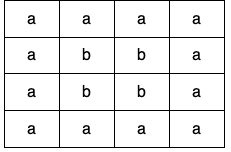
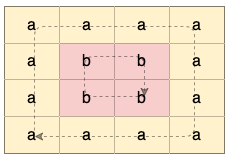
输入:grid = [["a","a","a","a"],["a","b","b","a"],["a","b","b","a"],["a","a","a","a"]] 输出:true 解释:如下图所示,有 2 个用不同颜色标出来的环:
示例 2:
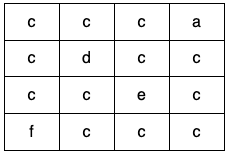
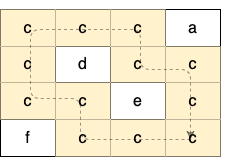
输入:grid = [["c","c","c","a"],["c","d","c","c"],["c","c","e","c"],["f","c","c","c"]] 输出:true 解释:如下图所示,只有高亮所示的一个合法环: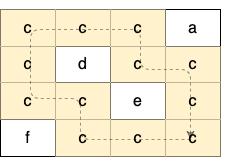
示例 3:
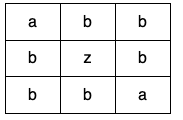
输入:grid = [["a","b","b"],["b","z","b"],["b","b","a"]] 输出:false
提示:
m == grid.lengthn == grid[i].length1 <= m <= 5001 <= n <= 500grid只包含小写英文字母。
构造并查集,遍历每个坐标 (i, j),如果下方或者右侧的元素 (x, y) 与当前元素 (i, j) 相同,进行合并操作。若是,若此前两个坐标已经处于连通状态,再进行合并时会形成环,直接返回 true。否则遍历结束返回 false。
并查集模板:
模板 1——朴素并查集:
# 初始化,p存储每个点的父节点
p = list(range(n))
# 返回x的祖宗节点
def find(x):
if p[x] != x:
# 路径压缩
p[x] = find(p[x])
return p[x]
# 合并a和b所在的两个集合
p[find(a)] = find(b)模板 2——维护 size 的并查集:
# 初始化,p存储每个点的父节点,size只有当节点是祖宗节点时才有意义,表示祖宗节点所在集合中,点的数量
p = list(range(n))
size = [1] * n
# 返回x的祖宗节点
def find(x):
if p[x] != x:
# 路径压缩
p[x] = find(p[x])
return p[x]
# 合并a和b所在的两个集合
if find(a) != find(b):
size[find(b)] += size[find(a)]
p[find(a)] = find(b)模板 3——维护到祖宗节点距离的并查集:
# 初始化,p存储每个点的父节点,d[x]存储x到p[x]的距离
p = list(range(n))
d = [0] * n
# 返回x的祖宗节点
def find(x):
if p[x] != x:
t = find(p[x])
d[x] += d[p[x]]
p[x] = t
return p[x]
# 合并a和b所在的两个集合
p[find(a)] = find(b)
d[find(a)] = distanceclass Solution:
def containsCycle(self, grid: List[List[str]]) -> bool:
def find(x):
if p[x] != x:
p[x] = find(p[x])
return p[x]
m, n = len(grid), len(grid[0])
p = list(range(m * n))
for i in range(m):
for j in range(n):
for a, b in [[0, 1], [1, 0]]:
x, y = i + a, j + b
if x < m and y < n and grid[x][y] == grid[i][j]:
if find(x * n + y) == find(i * n + j):
return True
p[find(x * n + y)] = find(i * n + j)
return Falseclass Solution {
private int[] p;
public boolean containsCycle(char[][] grid) {
int m = grid.length;
int n = grid[0].length;
p = new int[m * n];
for (int i = 0; i < p.length; ++i) {
p[i] = i;
}
int[] dirs = {0, 1, 0};
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
for (int k = 0; k < 2; ++k) {
int x = i + dirs[k];
int y = j + dirs[k + 1];
if (x < m && y < n && grid[i][j] == grid[x][y]) {
if (find(x * n + y) == find(i * n + j)) {
return true;
}
p[find(x * n + y)] = find(i * n + j);
}
}
}
}
return false;
}
private int find(int x) {
if (p[x] != x) {
p[x] = find(p[x]);
}
return p[x];
}
}class Solution {
public:
vector<int> p;
bool containsCycle(vector<vector<char>>& grid) {
int m = grid.size(), n = grid[0].size();
p.resize(m * n);
for (int i = 0; i < p.size(); ++i) p[i] = i;
vector<int> dirs = {0, 1, 0};
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
for (int k = 0; k < 2; ++k) {
int x = i + dirs[k], y = j + dirs[k + 1];
if (x < m && y < n && grid[x][y] == grid[i][j]) {
if (find(x * n + y) == find(i * n + j)) return 1;
p[find(x * n + y)] = find(i * n + j);
}
}
}
}
return 0;
}
int find(int x) {
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
};impl Solution {
#[allow(dead_code)]
pub fn contains_cycle(grid: Vec<Vec<char>>) -> bool {
let n = grid.len();
let m = grid[0].len();
let mut d_set: Vec<usize> = vec![0; n * m];
// Initialize the disjoint set
for i in 0..n * m {
d_set[i] = i;
}
// Traverse the grid
for i in 0..n {
for j in 0..m {
if i + 1 < n && grid[i + 1][j] == grid[i][j] {
// Check the below cell
let p_curr = Self::find(i * m + j, &mut d_set);
let p_below = Self::find((i + 1) * m + j, &mut d_set);
if p_curr == p_below {
return true;
}
// Otherwise, union the two cells
Self::union(p_curr, p_below, &mut d_set);
}
// Same to the right cell
if j + 1 < m && grid[i][j + 1] == grid[i][j] {
let p_curr = Self::find(i * m + j, &mut d_set);
let p_right = Self::find(i * m + (j + 1), &mut d_set);
if p_curr == p_right {
return true;
}
// Otherwise, union the two cells
Self::union(p_curr, p_right, &mut d_set);
}
}
}
false
}
#[allow(dead_code)]
fn find(x: usize, d_set: &mut Vec<usize>) -> usize {
if d_set[x] != x {
d_set[x] = Self::find(d_set[x], d_set);
}
d_set[x]
}
#[allow(dead_code)]
fn union(x: usize, y: usize, d_set: &mut Vec<usize>) {
let p_x = Self::find(x, d_set);
let p_y = Self::find(y, d_set);
d_set[p_x] = p_y;
}
}func containsCycle(grid [][]byte) bool {
m, n := len(grid), len(grid[0])
p := make([]int, m*n)
for i := range p {
p[i] = i
}
var find func(x int) int
find = func(x int) int {
if p[x] != x {
p[x] = find(p[x])
}
return p[x]
}
dirs := []int{1, 0, 1}
for i := 0; i < m; i++ {
for j := 0; j < n; j++ {
for k := 0; k < 2; k++ {
x, y := i+dirs[k], j+dirs[k+1]
if x < m && y < n && grid[x][y] == grid[i][j] {
if find(x*n+y) == find(i*n+j) {
return true
}
p[find(x*n+y)] = find(i*n + j)
}
}
}
}
return false
}/**
* @param {character[][]} grid
* @return {boolean}
*/
var containsCycle = function (grid) {
const m = grid.length;
const n = grid[0].length;
let p = Array.from({ length: m * n }, (_, i) => i);
function find(x) {
if (p[x] != x) {
p[x] = find(p[x]);
}
return p[x];
}
const dirs = [0, 1, 0];
for (let i = 0; i < m; ++i) {
for (let j = 0; j < n; ++j) {
for (let k = 0; k < 2; ++k) {
const x = i + dirs[k];
const y = j + dirs[k + 1];
if (x < m && y < n && grid[x][y] == grid[i][j]) {
if (find(x * n + y) == find(i * n + j)) {
return true;
}
p[find(x * n + y)] = find(i * n + j);
}
}
}
}
return false;
};