有 n 个网络节点,标记为 1 到 n。
给你一个列表 times,表示信号经过 有向 边的传递时间。 times[i] = (ui, vi, wi),其中 ui 是源节点,vi 是目标节点, wi 是一个信号从源节点传递到目标节点的时间。
现在,从某个节点 K 发出一个信号。需要多久才能使所有节点都收到信号?如果不能使所有节点收到信号,返回 -1 。
示例 1:
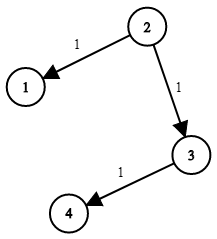
输入:times = [[2,1,1],[2,3,1],[3,4,1]], n = 4, k = 2 输出:2
示例 2:
输入:times = [[1,2,1]], n = 2, k = 1 输出:1
示例 3:
输入:times = [[1,2,1]], n = 2, k = 2 输出:-1
提示:
1 <= k <= n <= 1001 <= times.length <= 6000times[i].length == 31 <= ui, vi <= nui != vi0 <= wi <= 100- 所有
(ui, vi)对都 互不相同(即,不含重复边)
设 n 表示点数,m 表示边数。
方法一:朴素 Dijkstra 算法
时间复杂度
方法二:堆优化 Dijkstra 算法
时间复杂度
方法三:Bellman Ford 算法
时间复杂度
方法四:SPFA 算法
时间复杂度,平均情况下
朴素 Dijkstra 算法:
class Solution:
def networkDelayTime(self, times: List[List[int]], n: int, k: int) -> int:
INF = 0x3F3F
dist = [INF] * n
vis = [False] * n
g = [[INF] * n for _ in range(n)]
for u, v, w in times:
g[u - 1][v - 1] = w
dist[k - 1] = 0
for _ in range(n):
t = -1
for j in range(n):
if not vis[j] and (t == -1 or dist[t] > dist[j]):
t = j
vis[t] = True
for j in range(n):
dist[j] = min(dist[j], dist[t] + g[t][j])
ans = max(dist)
return -1 if ans == INF else ans堆优化 Dijkstra 算法:
class Solution:
def networkDelayTime(self, times: List[List[int]], n: int, k: int) -> int:
INF = 0x3F3F
g = defaultdict(list)
for u, v, w in times:
g[u - 1].append((v - 1, w))
dist = [INF] * n
dist[k - 1] = 0
q = [(0, k - 1)]
while q:
_, u = heappop(q)
for v, w in g[u]:
if dist[v] > dist[u] + w:
dist[v] = dist[u] + w
heappush(q, (dist[v], v))
ans = max(dist)
return -1 if ans == INF else ansBellman Ford 算法:
class Solution:
def networkDelayTime(self, times: List[List[int]], n: int, k: int) -> int:
INF = 0x3F3F
dist = [INF] * n
dist[k - 1] = 0
for _ in range(n):
backup = dist[:]
for u, v, w in times:
dist[v - 1] = min(dist[v - 1], dist[u - 1] + w)
ans = max(dist)
return -1 if ans == INF else ansSPFA 算法:
class Solution:
def networkDelayTime(self, times: List[List[int]], n: int, k: int) -> int:
INF = 0x3F3F
dist = [INF] * n
vis = [False] * n
g = defaultdict(list)
for u, v, w in times:
g[u - 1].append((v - 1, w))
k -= 1
dist[k] = 0
q = deque([k])
vis[k] = True
while q:
u = q.popleft()
vis[u] = False
for v, w in g[u]:
if dist[v] > dist[u] + w:
dist[v] = dist[u] + w
if not vis[v]:
q.append(v)
vis[v] = True
ans = max(dist)
return -1 if ans == INF else ans朴素 Dijkstra 算法:
class Solution {
private static final int INF = 0x3f3f;
public int networkDelayTime(int[][] times, int n, int k) {
int[][] g = new int[n][n];
int[] dist = new int[n];
boolean[] vis = new boolean[n];
for (int i = 0; i < n; ++i) {
dist[i] = INF;
Arrays.fill(g[i], INF);
}
for (int[] t : times) {
g[t[0] - 1][t[1] - 1] = t[2];
}
dist[k - 1] = 0;
for (int i = 0; i < n; ++i) {
int t = -1;
for (int j = 0; j < n; ++j) {
if (!vis[j] && (t == -1 || dist[t] > dist[j])) {
t = j;
}
}
vis[t] = true;
for (int j = 0; j < n; ++j) {
dist[j] = Math.min(dist[j], dist[t] + g[t][j]);
}
}
int ans = 0;
for (int d : dist) {
ans = Math.max(ans, d);
}
return ans == INF ? -1 : ans;
}
}堆优化 Dijkstra 算法:
class Solution {
private static final int INF = 0x3f3f;
public int networkDelayTime(int[][] times, int n, int k) {
List<int[]>[] g = new List[n];
int[] dist = new int[n];
for (int i = 0; i < n; ++i) {
dist[i] = INF;
g[i] = new ArrayList<>();
}
for (int[] t : times) {
g[t[0] - 1].add(new int[] {t[1] - 1, t[2]});
}
dist[k - 1] = 0;
PriorityQueue<int[]> q = new PriorityQueue<>(Comparator.comparingInt(a -> a[0]));
q.offer(new int[] {0, k - 1});
while (!q.isEmpty()) {
int[] p = q.poll();
int u = p[1];
for (int[] ne : g[u]) {
int v = ne[0], w = ne[1];
if (dist[v] > dist[u] + w) {
dist[v] = dist[u] + w;
q.offer(new int[] {dist[v], v});
}
}
}
int ans = 0;
for (int d : dist) {
ans = Math.max(ans, d);
}
return ans == INF ? -1 : ans;
}
}Bellman Ford 算法:
class Solution {
private static final int INF = 0x3f3f;
public int networkDelayTime(int[][] times, int n, int k) {
int[] dist = new int[n];
int[] backup = new int[n];
Arrays.fill(dist, INF);
dist[k - 1] = 0;
for (int i = 0; i < n; ++i) {
System.arraycopy(dist, 0, backup, 0, n);
for (int[] t : times) {
int u = t[0] - 1, v = t[1] - 1, w = t[2];
dist[v] = Math.min(dist[v], backup[u] + w);
}
}
int ans = 0;
for (int i = 0; i < n; ++i) {
ans = Math.max(ans, dist[i]);
}
return ans == INF ? -1 : ans;
}
}SPFA 算法:
class Solution {
private static final int INF = 0x3f3f;
public int networkDelayTime(int[][] times, int n, int k) {
int[] dist = new int[n];
boolean[] vis = new boolean[n];
List<int[]>[] g = new List[n];
for (int i = 0; i < n; ++i) {
dist[i] = INF;
g[i] = new ArrayList<>();
}
for (int[] t : times) {
int u = t[0] - 1, v = t[1] - 1, w = t[2];
g[u].add(new int[] {v, w});
}
--k;
dist[k] = 0;
Deque<Integer> q = new ArrayDeque<>();
q.offer(k);
vis[k] = true;
while (!q.isEmpty()) {
int u = q.poll();
vis[u] = false;
for (int[] ne : g[u]) {
int v = ne[0], w = ne[1];
if (dist[v] > dist[u] + w) {
dist[v] = dist[u] + w;
if (!vis[v]) {
q.offer(v);
vis[v] = true;
}
}
}
}
int ans = 0;
for (int i = 0; i < n; ++i) {
ans = Math.max(ans, dist[i]);
}
return ans == INF ? -1 : ans;
}
}朴素 Dijkstra 算法:
func networkDelayTime(times [][]int, n int, k int) int {
const inf = 0x3f3f
dist := make([]int, n)
vis := make([]bool, n)
g := make([][]int, n)
for i := range dist {
dist[i] = inf
g[i] = make([]int, n)
for j := range g[i] {
g[i][j] = inf
}
}
for _, t := range times {
g[t[0]-1][t[1]-1] = t[2]
}
dist[k-1] = 0
for i := 0; i < n; i++ {
t := -1
for j := 0; j < n; j++ {
if !vis[j] && (t == -1 || dist[t] > dist[j]) {
t = j
}
}
vis[t] = true
for j := 0; j < n; j++ {
dist[j] = min(dist[j], dist[t]+g[t][j])
}
}
ans := slices.Max(dist)
if ans == inf {
return -1
}
return ans
}堆优化 Dijkstra 算法:
const Inf = 0x3f3f3f3f
type pair struct {
first int
second int
}
var _ heap.Interface = (*pairs)(nil)
type pairs []pair
func (a pairs) Len() int { return len(a) }
func (a pairs) Less(i int, j int) bool {
return a[i].first < a[j].first || a[i].first == a[j].first && a[i].second < a[j].second
}
func (a pairs) Swap(i int, j int) { a[i], a[j] = a[j], a[i] }
func (a *pairs) Push(x any) { *a = append(*a, x.(pair)) }
func (a *pairs) Pop() any { l := len(*a); t := (*a)[l-1]; *a = (*a)[:l-1]; return t }
func networkDelayTime(times [][]int, n int, k int) int {
graph := make([]pairs, n)
for _, time := range times {
from, to, time := time[0]-1, time[1]-1, time[2]
graph[from] = append(graph[from], pair{to, time})
}
dis := make([]int, n)
for i := range dis {
dis[i] = Inf
}
dis[k-1] = 0
vis := make([]bool, n)
h := make(pairs, 0)
heap.Push(&h, pair{0, k - 1})
for len(h) > 0 {
from := heap.Pop(&h).(pair).second
if vis[from] {
continue
}
vis[from] = true
for _, e := range graph[from] {
to, d := e.first, dis[from]+e.second
if d < dis[to] {
dis[to] = d
heap.Push(&h, pair{d, to})
}
}
}
ans := slices.Max(dis)
if ans == Inf {
return -1
}
return ans
}Bellman Ford 算法:
func networkDelayTime(times [][]int, n int, k int) int {
const inf = 0x3f3f
dist := make([]int, n)
backup := make([]int, n)
for i := range dist {
dist[i] = inf
}
dist[k-1] = 0
for i := 0; i < n; i++ {
copy(backup, dist)
for _, e := range times {
u, v, w := e[0]-1, e[1]-1, e[2]
dist[v] = min(dist[v], backup[u]+w)
}
}
ans := slices.Max(dist)
if ans == inf {
return -1
}
return ans
}SPFA 算法:
func networkDelayTime(times [][]int, n int, k int) int {
const inf = 0x3f3f
dist := make([]int, n)
vis := make([]bool, n)
g := make([][][]int, n)
for i := range dist {
dist[i] = inf
}
for _, t := range times {
u, v, w := t[0]-1, t[1]-1, t[2]
g[u] = append(g[u], []int{v, w})
}
k--
dist[k] = 0
q := []int{k}
vis[k] = true
for len(q) > 0 {
u := q[0]
q = q[1:]
vis[u] = false
for _, ne := range g[u] {
v, w := ne[0], ne[1]
if dist[v] > dist[u]+w {
dist[v] = dist[u] + w
if !vis[v] {
q = append(q, v)
vis[v] = true
}
}
}
}
ans := slices.Max(dist)
if ans == inf {
return -1
}
return ans
}朴素 Dijkstra 算法:
class Solution {
public:
const int inf = 0x3f3f;
int networkDelayTime(vector<vector<int>>& times, int n, int k) {
vector<vector<int>> g(n, vector<int>(n, inf));
for (auto& t : times) g[t[0] - 1][t[1] - 1] = t[2];
vector<bool> vis(n);
vector<int> dist(n, inf);
dist[k - 1] = 0;
for (int i = 0; i < n; ++i) {
int t = -1;
for (int j = 0; j < n; ++j) {
if (!vis[j] && (t == -1 || dist[t] > dist[j])) {
t = j;
}
}
vis[t] = true;
for (int j = 0; j < n; ++j) {
dist[j] = min(dist[j], dist[t] + g[t][j]);
}
}
int ans = *max_element(dist.begin(), dist.end());
return ans == inf ? -1 : ans;
}
};堆优化 Dijkstra 算法:
class Solution {
public:
const int inf = 0x3f3f;
int networkDelayTime(vector<vector<int>>& times, int n, int k) {
vector<vector<vector<int>>> g(n);
for (auto& t : times) g[t[0] - 1].push_back({t[1] - 1, t[2]});
vector<int> dist(n, inf);
dist[k - 1] = 0;
priority_queue<vector<int>, vector<vector<int>>, greater<vector<int>>> q;
q.push({0, k - 1});
while (!q.empty()) {
auto p = q.top();
q.pop();
int u = p[1];
for (auto& ne : g[u]) {
int v = ne[0], w = ne[1];
if (dist[v] > dist[u] + w) {
dist[v] = dist[u] + w;
q.push({dist[v], v});
}
}
}
int ans = *max_element(dist.begin(), dist.end());
return ans == inf ? -1 : ans;
}
};Bellman Ford 算法:
class Solution {
public:
int inf = 0x3f3f;
int networkDelayTime(vector<vector<int>>& times, int n, int k) {
vector<int> dist(n, inf);
dist[k - 1] = 0;
for (int i = 0; i < n; ++i) {
vector<int> backup = dist;
for (auto& e : times) {
int u = e[0] - 1, v = e[1] - 1, w = e[2];
dist[v] = min(dist[v], backup[u] + w);
}
}
int ans = *max_element(dist.begin(), dist.end());
return ans == inf ? -1 : ans;
}
};SPFA 算法:
class Solution {
public:
const int inf = 0x3f3f;
int networkDelayTime(vector<vector<int>>& times, int n, int k) {
vector<int> dist(n, inf);
vector<vector<vector<int>>> g(n);
for (auto& e : times) {
int u = e[0] - 1, v = e[1] - 1, w = e[2];
g[u].push_back({v, w});
}
vector<bool> vis(n);
--k;
queue<int> q{{k}};
vis[k] = true;
dist[k] = 0;
while (!q.empty()) {
int u = q.front();
q.pop();
vis[u] = false;
for (auto& ne : g[u]) {
int v = ne[0], w = ne[1];
if (dist[v] > dist[u] + w) {
dist[v] = dist[u] + w;
if (!vis[v]) {
q.push(v);
vis[v] = true;
}
}
}
}
int ans = *max_element(dist.begin(), dist.end());
return ans == inf ? -1 : ans;
}
};