给定一个 m x n 整数矩阵 matrix ,找出其中 最长递增路径 的长度。
对于每个单元格,你可以往上,下,左,右四个方向移动。 你 不能 在 对角线 方向上移动或移动到 边界外(即不允许环绕)。
示例 1:
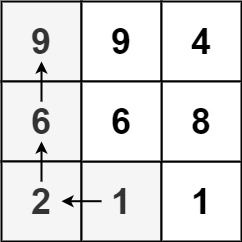
输入:matrix = [[9,9,4],[6,6,8],[2,1,1]]
输出:4
解释:最长递增路径为 [1, 2, 6, 9]。
示例 2:
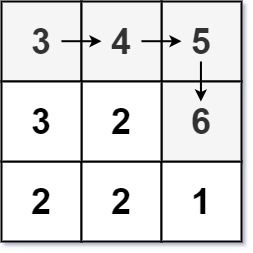
输入:matrix = [[3,4,5],[3,2,6],[2,2,1]]
输出:4
解释:最长递增路径是 [3, 4, 5, 6]。注意不允许在对角线方向上移动。
示例 3:
输入:matrix = [[1]] 输出:1
提示:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 2000 <= matrix[i][j] <= 231 - 1
方法一:记忆化搜索
我们设计一个函数
函数
- 如果
$(i, j)$ 已经被访问过,直接返回$\textit{f}(i, j)$ ; - 否则对
$(i, j)$ 进行搜索,搜索四个方向的坐标$(x, y)$ ,如果满足$0 \le x < m, 0 \le y < n$ 以及$matrix[x][y] \gt matrix[i][j]$ ,那么对$(x, y)$ 进行搜索。搜索结束后,将$\textit{f}(i, j)$ 更新为$\textit{f}(i, j) = \max(\textit{f}(i, j), \textit{f}(x, y) + 1)$ 。最后返回$\textit{f}(i, j)$ 。
时间复杂度
相似题目:2328. 网格图中递增路径的数目。
class Solution:
def longestIncreasingPath(self, matrix: List[List[int]]) -> int:
@cache
def dfs(i: int, j: int) -> int:
ans = 0
for a, b in pairwise((-1, 0, 1, 0, -1)):
x, y = i + a, j + b
if 0 <= x < m and 0 <= y < n and matrix[x][y] > matrix[i][j]:
ans = max(ans, dfs(x, y))
return ans + 1
m, n = len(matrix), len(matrix[0])
return max(dfs(i, j) for i in range(m) for j in range(n))class Solution {
private int m;
private int n;
private int[][] matrix;
private int[][] f;
public int longestIncreasingPath(int[][] matrix) {
m = matrix.length;
n = matrix[0].length;
f = new int[m][n];
this.matrix = matrix;
int ans = 0;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
ans = Math.max(ans, dfs(i, j));
}
}
return ans;
}
private int dfs(int i, int j) {
if (f[i][j] != 0) {
return f[i][j];
}
int[] dirs = {-1, 0, 1, 0, -1};
for (int k = 0; k < 4; ++k) {
int x = i + dirs[k];
int y = j + dirs[k + 1];
if (x >= 0 && x < m && y >= 0 && y < n && matrix[x][y] > matrix[i][j]) {
f[i][j] = Math.max(f[i][j], dfs(x, y));
}
}
return ++f[i][j];
}
}class Solution {
public:
int longestIncreasingPath(vector<vector<int>>& matrix) {
int m = matrix.size(), n = matrix[0].size();
int f[m][n];
memset(f, 0, sizeof(f));
int ans = 0;
int dirs[5] = {-1, 0, 1, 0, -1};
function<int(int, int)> dfs = [&](int i, int j) -> int {
if (f[i][j]) {
return f[i][j];
}
for (int k = 0; k < 4; ++k) {
int x = i + dirs[k], y = j + dirs[k + 1];
if (x >= 0 && x < m && y >= 0 && y < n && matrix[x][y] > matrix[i][j]) {
f[i][j] = max(f[i][j], dfs(x, y));
}
}
return ++f[i][j];
};
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
ans = max(ans, dfs(i, j));
}
}
return ans;
}
};func longestIncreasingPath(matrix [][]int) (ans int) {
m, n := len(matrix), len(matrix[0])
f := make([][]int, m)
for i := range f {
f[i] = make([]int, n)
}
dirs := [5]int{-1, 0, 1, 0, -1}
var dfs func(i, j int) int
dfs = func(i, j int) int {
if f[i][j] != 0 {
return f[i][j]
}
for k := 0; k < 4; k++ {
x, y := i+dirs[k], j+dirs[k+1]
if 0 <= x && x < m && 0 <= y && y < n && matrix[x][y] > matrix[i][j] {
f[i][j] = max(f[i][j], dfs(x, y))
}
}
f[i][j]++
return f[i][j]
}
for i := 0; i < m; i++ {
for j := 0; j < n; j++ {
ans = max(ans, dfs(i, j))
}
}
return
}function longestIncreasingPath(matrix: number[][]): number {
const m = matrix.length;
const n = matrix[0].length;
const f: number[][] = Array(m)
.fill(0)
.map(() => Array(n).fill(0));
const dirs = [-1, 0, 1, 0, -1];
const dfs = (i: number, j: number): number => {
if (f[i][j] > 0) {
return f[i][j];
}
for (let k = 0; k < 4; ++k) {
const x = i + dirs[k];
const y = j + dirs[k + 1];
if (x >= 0 && x < m && y >= 0 && y < n && matrix[x][y] > matrix[i][j]) {
f[i][j] = Math.max(f[i][j], dfs(x, y));
}
}
return ++f[i][j];
};
let ans = 0;
for (let i = 0; i < m; ++i) {
for (let j = 0; j < n; ++j) {
ans = Math.max(ans, dfs(i, j));
}
}
return ans;
}