参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
《代码随想录》算法视频公开课:讲透二叉树的层序遍历 | 广度优先搜索 | LeetCode:102.二叉树的层序遍历,相信结合视频再看本篇题解,更有助于大家对本题的理解。
学会二叉树的层序遍历,可以一口气打完以下十题:
- 102.二叉树的层序遍历
- 107.二叉树的层次遍历II
- 199.二叉树的右视图
- 637.二叉树的层平均值
- 429.N叉树的层序遍历
- 515.在每个树行中找最大值
- 116.填充每个节点的下一个右侧节点指针
- 117.填充每个节点的下一个右侧节点指针II
- 104.二叉树的最大深度
- 111.二叉树的最小深度
给你一个二叉树,请你返回其按 层序遍历 得到的节点值。 (即逐层地,从左到右访问所有节点)。
我们之前讲过了三篇关于二叉树的深度优先遍历的文章:
接下来我们再来介绍二叉树的另一种遍历方式:层序遍历。
层序遍历一个二叉树。就是从左到右一层一层的去遍历二叉树。这种遍历的方式和我们之前讲过的都不太一样。
需要借用一个辅助数据结构即队列来实现,队列先进先出,符合一层一层遍历的逻辑,而用栈先进后出适合模拟深度优先遍历也就是递归的逻辑。
而这种层序遍历方式就是图论中的广度优先遍历,只不过我们应用在二叉树上。
使用队列实现二叉树广度优先遍历,动画如下:
这样就实现了层序从左到右遍历二叉树。
代码如下:这份代码也可以作为二叉树层序遍历的模板,打十个就靠它了。
c++代码如下:
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
queue<TreeNode*> que;
if (root != NULL) que.push(root);
vector<vector<int>> result;
while (!que.empty()) {
int size = que.size();
vector<int> vec;
// 这里一定要使用固定大小size,不要使用que.size(),因为que.size是不断变化的
for (int i = 0; i < size; i++) {
TreeNode* node = que.front();
que.pop();
vec.push_back(node->val);
if (node->left) que.push(node->left);
if (node->right) que.push(node->right);
}
result.push_back(vec);
}
return result;
}
};# 递归法
class Solution {
public:
void order(TreeNode* cur, vector<vector<int>>& result, int depth)
{
if (cur == nullptr) return;
if (result.size() == depth) result.push_back(vector<int>());
result[depth].push_back(cur->val);
order(cur->left, result, depth + 1);
order(cur->right, result, depth + 1);
}
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> result;
int depth = 0;
order(root, result, depth);
return result;
}
};// 102.二叉树的层序遍历
class Solution {
public List<List<Integer>> resList = new ArrayList<List<Integer>>();
public List<List<Integer>> levelOrder(TreeNode root) {
//checkFun01(root,0);
checkFun02(root);
return resList;
}
//BFS--递归方式
public void checkFun01(TreeNode node, Integer deep) {
if (node == null) return;
deep++;
if (resList.size() < deep) {
//当层级增加时,list的Item也增加,利用list的索引值进行层级界定
List<Integer> item = new ArrayList<Integer>();
resList.add(item);
}
resList.get(deep - 1).add(node.val);
checkFun01(node.left, deep);
checkFun01(node.right, deep);
}
//BFS--迭代方式--借助队列
public void checkFun02(TreeNode node) {
if (node == null) return;
Queue<TreeNode> que = new LinkedList<TreeNode>();
que.offer(node);
while (!que.isEmpty()) {
List<Integer> itemList = new ArrayList<Integer>();
int len = que.size();
while (len > 0) {
TreeNode tmpNode = que.poll();
itemList.add(tmpNode.val);
if (tmpNode.left != null) que.offer(tmpNode.left);
if (tmpNode.right != null) que.offer(tmpNode.right);
len--;
}
resList.add(itemList);
}
}
}# 利用长度法
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
if not root:
return []
queue = collections.deque([root])
result = []
while queue:
level = []
for _ in range(len(queue)):
cur = queue.popleft()
level.append(cur.val)
if cur.left:
queue.append(cur.left)
if cur.right:
queue.append(cur.right)
result.append(level)
return result#递归法
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
if not root:
return []
levels = []
def traverse(node, level):
if not node:
return
if len(levels) == level:
levels.append([])
levels[level].append(node.val)
traverse(node.left, level + 1)
traverse(node.right, level + 1)
traverse(root, 0)
return levels/**
102. 二叉树的递归遍历
*/
func levelOrder(root *TreeNode) [][]int {
arr := [][]int{}
depth := 0
var order func(root *TreeNode, depth int)
order = func(root *TreeNode, depth int) {
if root == nil {
return
}
if len(arr) == depth {
arr = append(arr, []int{})
}
arr[depth] = append(arr[depth], root.Val)
order(root.Left, depth+1)
order(root.Right, depth+1)
}
order(root, depth)
return arr
}/**
102. 二叉树的层序遍历 使用container包
*/
func levelOrder(root *TreeNode) [][]int {
res := [][]int{}
if root == nil{//防止为空
return res
}
queue := list.New()
queue.PushBack(root)
var tmpArr []int
for queue.Len() > 0 {
length := queue.Len() //保存当前层的长度,然后处理当前层(十分重要,防止添加下层元素影响判断层中元素的个数)
for i := 0; i < length; i++ {
node := queue.Remove(queue.Front()).(*TreeNode) //出队列
if node.Left != nil {
queue.PushBack(node.Left)
}
if node.Right != nil {
queue.PushBack(node.Right)
}
tmpArr = append(tmpArr, node.Val) //将值加入本层切片中
}
res = append(res, tmpArr) //放入结果集
tmpArr = []int{} //清空层的数据
}
return res
}
/**
102. 二叉树的层序遍历 使用切片
*/
func levelOrder(root *TreeNode) [][]int {
res := make([][]int, 0)
if root == nil {
return res
}
queue := make([]*TreeNode, 0)
queue = append(queue, root)
for len(queue) > 0 {
size := len(queue)
level := make([]int, 0)
for i := 0; i < size; i++ {
node := queue[0]
queue = queue[1:]
level = append(level, node.Val)
if node.Left != nil {
queue = append(queue, node.Left)
}
if node.Right != nil {
queue = append(queue, node.Right)
}
}
res = append(res, level)
}
return res
}
/**
102. 二叉树的层序遍历:使用切片模拟队列,易理解
*/
func levelOrder(root *TreeNode) (res [][]int) {
if root == nil {
return
}
curLevel := []*TreeNode{root} // 存放当前层节点
for len(curLevel) > 0 {
nextLevel := []*TreeNode{} // 准备通过当前层生成下一层
vals := []int{}
for _, node := range curLevel {
vals = append(vals, node.Val) // 收集当前层的值
// 收集下一层的节点
if node.Left != nil {
nextLevel = append(nextLevel, node.Left)
}
if node.Right != nil {
nextLevel = append(nextLevel, node.Right)
}
}
res = append(res, vals)
curLevel = nextLevel // 将下一层变成当前层
}
return
}var levelOrder = function(root) {
//二叉树的层序遍历
let res = [], queue = [];
queue.push(root);
if(root === null) {
return res;
}
while(queue.length !== 0) {
// 记录当前层级节点数
let length = queue.length;
//存放每一层的节点
let curLevel = [];
for(let i = 0;i < length; i++) {
let node = queue.shift();
curLevel.push(node.val);
// 存放当前层下一层的节点
node.left && queue.push(node.left);
node.right && queue.push(node.right);
}
//把每一层的结果放到结果数组
res.push(curLevel);
}
return res;
};function levelOrder(root: TreeNode | null): number[][] {
let helperQueue: TreeNode[] = [];
let res: number[][] = [];
let tempArr: number[] = [];
if (root !== null) helperQueue.push(root);
let curNode: TreeNode;
while (helperQueue.length > 0) {
for (let i = 0, length = helperQueue.length; i < length; i++) {
curNode = helperQueue.shift()!;
tempArr.push(curNode.val);
if (curNode.left !== null) {
helperQueue.push(curNode.left);
}
if (curNode.right !== null) {
helperQueue.push(curNode.right);
}
}
res.push(tempArr);
tempArr = [];
}
return res;
};func levelOrder(_ root: TreeNode?) -> [[Int]] {
var result = [[Int]]()
guard let root = root else { return result }
// 表示一层
var queue = [root]
while !queue.isEmpty {
let count = queue.count
var subarray = [Int]()
for _ in 0 ..< count {
// 当前层
let node = queue.removeFirst()
subarray.append(node.val)
// 下一层
if let node = node.left { queue.append(node) }
if let node = node.right { queue.append(node) }
}
result.append(subarray)
}
return result
}// 102.二叉树的层序遍历
object Solution {
import scala.collection.mutable
def levelOrder(root: TreeNode): List[List[Int]] = {
val res = mutable.ListBuffer[List[Int]]()
if (root == null) return res.toList
val queue = mutable.Queue[TreeNode]() // 声明一个队列
queue.enqueue(root) // 把根节点加入queue
while (!queue.isEmpty) {
val tmp = mutable.ListBuffer[Int]()
val len = queue.size // 求出len的长度
for (i <- 0 until len) { // 从0到当前队列长度的所有节点都加入到结果集
val curNode = queue.dequeue()
tmp.append(curNode.value)
if (curNode.left != null) queue.enqueue(curNode.left)
if (curNode.right != null) queue.enqueue(curNode.right)
}
res.append(tmp.toList)
}
res.toList
}
}use std::cell::RefCell;
use std::rc::Rc;
use std::collections::VecDeque;
impl Solution {
pub fn level_order(root: Option<Rc<RefCell<TreeNode>>>) -> Vec<Vec<i32>> {
let mut res = vec![];
let mut queue = VecDeque::new();
if root.is_some() {
queue.push_back(root);
}
while !queue.is_empty() {
let mut temp = vec![];
for _ in 0..queue.len() {
let node = queue.pop_front().unwrap().unwrap();
temp.push(node.borrow().val);
if node.borrow().left.is_some() {
queue.push_back(node.borrow().left.clone());
}
if node.borrow().right.is_some() {
queue.push_back(node.borrow().right.clone());
}
}
res.push(temp);
}
res
}
}public IList<IList<int>> LevelOrder(TreeNode root)
{
var res = new List<IList<int>>();
var que = new Queue<TreeNode>();
if (root == null) return res;
que.Enqueue(root);
while (que.Count != 0)
{
var size = que.Count;
var vec = new List<int>();
for (int i = 0; i < size; i++)
{
var cur = que.Dequeue();
vec.Add(cur.val);
if (cur.left != null) que.Enqueue(cur.left);
if (cur.right != null) que.Enqueue(cur.right);
}
res.Add(vec);
}
return res;
}此时我们就掌握了二叉树的层序遍历了,那么如下九道力扣上的题目,只需要修改模板的两三行代码(不能再多了),便可打倒!
给定一个二叉树,返回其节点值自底向上的层次遍历。 (即按从叶子节点所在层到根节点所在的层,逐层从左向右遍历)
相对于102.二叉树的层序遍历,就是最后把result数组反转一下就可以了。
C++代码:
class Solution {
public:
vector<vector<int>> levelOrderBottom(TreeNode* root) {
queue<TreeNode*> que;
if (root != NULL) que.push(root);
vector<vector<int>> result;
while (!que.empty()) {
int size = que.size();
vector<int> vec;
for (int i = 0; i < size; i++) {
TreeNode* node = que.front();
que.pop();
vec.push_back(node->val);
if (node->left) que.push(node->left);
if (node->right) que.push(node->right);
}
result.push_back(vec);
}
reverse(result.begin(), result.end()); // 在这里反转一下数组即可
return result;
}
};class Solution:
"""二叉树层序遍历II迭代解法"""
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def levelOrderBottom(self, root: TreeNode) -> List[List[int]]:
if not root:
return []
queue = collections.deque([root])
result = []
while queue:
level = []
for _ in range(len(queue)):
cur = queue.popleft()
level.append(cur.val)
if cur.left:
queue.append(cur.left)
if cur.right:
queue.append(cur.right)
result.append(level)
return result[::-1]// 107. 二叉树的层序遍历 II
public class N0107 {
/**
* 解法:队列,迭代。
* 层序遍历,再翻转数组即可。
*/
public List<List<Integer>> solution1(TreeNode root) {
List<List<Integer>> list = new ArrayList<>();
Deque<TreeNode> que = new LinkedList<>();
if (root == null) {
return list;
}
que.offerLast(root);
while (!que.isEmpty()) {
List<Integer> levelList = new ArrayList<>();
int levelSize = que.size();
for (int i = 0; i < levelSize; i++) {
TreeNode peek = que.peekFirst();
levelList.add(que.pollFirst().val);
if (peek.left != null) {
que.offerLast(peek.left);
}
if (peek.right != null) {
que.offerLast(peek.right);
}
}
list.add(levelList);
}
List<List<Integer>> result = new ArrayList<>();
for (int i = list.size() - 1; i >= 0; i-- ) {
result.add(list.get(i));
}
return result;
}
}/**
* 思路和模板相同, 对收集答案的方式做了优化, 最后不需要反转
*/
class Solution {
public List<List<Integer>> levelOrderBottom(TreeNode root) {
// 利用链表可以进行 O(1) 头部插入, 这样最后答案不需要再反转
LinkedList<List<Integer>> ans = new LinkedList<>();
Queue<TreeNode> q = new LinkedList<>();
if (root != null) q.offer(root);
while (!q.isEmpty()) {
int size = q.size();
List<Integer> temp = new ArrayList<>();
for (int i = 0; i < size; i ++) {
TreeNode node = q.poll();
temp.add(node.val);
if (node.left != null) q.offer(node.left);
if (node.right != null) q.offer(node.right);
}
// 新遍历到的层插到头部, 这样就满足按照层次反序的要求
ans.addFirst(temp);
}
return ans;
}/**
107. 二叉树的层序遍历 II
*/
func levelOrderBottom(root *TreeNode) [][]int {
queue := list.New()
res := [][]int{}
if root == nil{
return res
}
queue.PushBack(root)
for queue.Len() > 0 {
length := queue.Len()
tmp := []int{}
for i := 0; i < length; i++ {
node := queue.Remove(queue.Front()).(*TreeNode)
if node.Left != nil {
queue.PushBack(node.Left)
}
if node.Right != nil {
queue.PushBack(node.Right)
}
tmp = append(tmp, node.Val)
}
res=append(res, tmp)
}
//反转结果集
for i:=0; i<len(res)/2; i++ {
res[i], res[len(res)-i-1] = res[len(res)-i-1], res[i]
}
return res
}// 使用切片作为队列
func levelOrderBottom(root *TreeNode) [][]int {
res := make([][]int, 0)
if root == nil {
return res
}
queue := make([]*TreeNode, 0)
queue = append(queue, root)
for len(queue) > 0 {
size := len(queue)
level := make([]int, 0)
for i := 0; i < size; i++ {
node := queue[0]
queue = queue[1:]
level = append(level, node.Val)
if node.Left != nil {
queue = append(queue, node.Left)
}
if node.Right != nil {
queue = append(queue, node.Right)
}
}
res = append(res, level)
}
l, r := 0, len(res)-1
for l < r {
res[l], res[r] = res[r], res[l]
l++
r--
}
return res
}var levelOrderBottom = function (root) {
let res = [],
queue = [];
queue.push(root);
while (queue.length && root !== null) {
// 存放当前层级节点数组
let curLevel = [];
// 计算当前层级节点数量
let length = queue.length;
while (length--) {
let node = queue.shift();
// 把当前层节点存入curLevel数组
curLevel.push(node.val);
// 把下一层级的左右节点存入queue队列
node.left && queue.push(node.left);
node.right && queue.push(node.right);
}
// 从数组前头插入值,避免最后反转数组,减少运算时间
res.unshift(curLevel);
}
return res;
};function levelOrderBottom(root: TreeNode | null): number[][] {
let helperQueue: TreeNode[] = [];
let resArr: number[][] = [];
let tempArr: number[] = [];
let tempNode: TreeNode;
if (root !== null) helperQueue.push(root);
while (helperQueue.length > 0) {
for (let i = 0, length = helperQueue.length; i < length; i++) {
tempNode = helperQueue.shift()!;
tempArr.push(tempNode.val);
if (tempNode.left !== null) helperQueue.push(tempNode.left);
if (tempNode.right !== null) helperQueue.push(tempNode.right);
}
resArr.push(tempArr);
tempArr = [];
}
return resArr.reverse();
};func levelOrderBottom(_ root: TreeNode?) -> [[Int]] {
// 表示一层
var queue = [TreeNode]()
if let node = root { queue.append(node) }
var result = [[Int]]()
while !queue.isEmpty {
let count = queue.count
var subarray = [Int]()
for _ in 0 ..< count {
// 当前层
let node = queue.removeFirst()
subarray.append(node.val)
// 下一层
if let node = node.left { queue.append(node) }
if let node = node.right { queue.append(node)}
}
result.append(subarray)
}
return result.reversed()
}// 107.二叉树的层次遍历II
object Solution {
import scala.collection.mutable
def levelOrderBottom(root: TreeNode): List[List[Int]] = {
val res = mutable.ListBuffer[List[Int]]()
if (root == null) return res.toList
val queue = mutable.Queue[TreeNode]()
queue.enqueue(root)
while (!queue.isEmpty) {
val tmp = mutable.ListBuffer[Int]()
val len = queue.size
for (i <- 0 until len) {
val curNode = queue.dequeue()
tmp.append(curNode.value)
if (curNode.left != null) queue.enqueue(curNode.left)
if (curNode.right != null) queue.enqueue(curNode.right)
}
res.append(tmp.toList)
}
// 最后翻转一下
res.reverse.toList
}
use std::cell::RefCell;
use std::collections::VecDeque;
use std::rc::Rc;
impl Solution {
pub fn level_order_bottom(root: Option<Rc<RefCell<TreeNode>>>) -> Vec<Vec<i32>> {
let mut res = vec![];
let mut queue = VecDeque::new();
if root.is_some() {
queue.push_back(root);
}
while !queue.is_empty() {
let mut temp = vec![];
for _ in 0..queue.len() {
let node = queue.pop_front().unwrap().unwrap();
temp.push(node.borrow().val);
if node.borrow().left.is_some() {
queue.push_back(node.borrow().left.clone());
}
if node.borrow().right.is_some() {
queue.push_back(node.borrow().right.clone());
}
}
res.push(temp);
}
res.into_iter().rev().collect()
}
}public IList<IList<int>> LevelOrderBottom(TreeNode root)
{
var res = new List<IList<int>>();
var que = new Queue<TreeNode>();
if (root == null) return res;
que.Enqueue(root);
while (que.Count != 0)
{
var size = que.Count;
var vec = new List<int>();
for (int i = 0; i < size; i++)
{
var cur = que.Dequeue();
vec.Add(cur.val);
if (cur.left != null) que.Enqueue(cur.left);
if (cur.right != null) que.Enqueue(cur.right);
}
res.Add(vec);
}
res.Reverse();
return res;
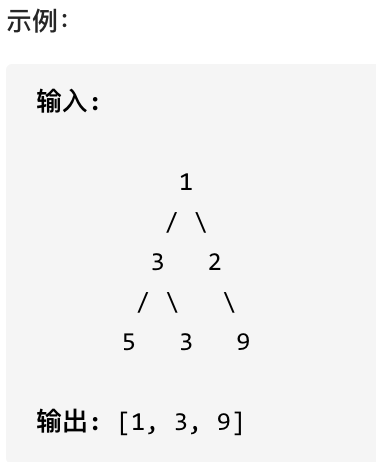
}给定一棵二叉树,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
层序遍历的时候,判断是否遍历到单层的最后面的元素,如果是,就放进result数组中,随后返回result就可以了。
C++代码:
class Solution {
public:
vector<int> rightSideView(TreeNode* root) {
queue<TreeNode*> que;
if (root != NULL) que.push(root);
vector<int> result;
while (!que.empty()) {
int size = que.size();
for (int i = 0; i < size; i++) {
TreeNode* node = que.front();
que.pop();
if (i == (size - 1)) result.push_back(node->val); // 将每一层的最后元素放入result数组中
if (node->left) que.push(node->left);
if (node->right) que.push(node->right);
}
}
return result;
}
};# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def rightSideView(self, root: TreeNode) -> List[int]:
if not root:
return []
queue = collections.deque([root])
right_view = []
while queue:
level_size = len(queue)
for i in range(level_size):
node = queue.popleft()
if i == level_size - 1:
right_view.append(node.val)
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
return right_view// 199.二叉树的右视图
public class N0199 {
/**
* 解法:队列,迭代。
* 每次返回每层的最后一个字段即可。
*
* 小优化:每层右孩子先入队。代码略。
*/
public List<Integer> rightSideView(TreeNode root) {
List<Integer> list = new ArrayList<>();
Deque<TreeNode> que = new LinkedList<>();
if (root == null) {
return list;
}
que.offerLast(root);
while (!que.isEmpty()) {
int levelSize = que.size();
for (int i = 0; i < levelSize; i++) {
TreeNode poll = que.pollFirst();
if (poll.left != null) {
que.addLast(poll.left);
}
if (poll.right != null) {
que.addLast(poll.right);
}
if (i == levelSize - 1) {
list.add(poll.val);
}
}
}
return list;
}
}/**
199. 二叉树的右视图
*/
func rightSideView(root *TreeNode) []int {
if root == nil {
return nil
}
res := make([]int, 0)
queue := list.New()
queue.PushBack(root)
for queue.Len() > 0 {
length := queue.Len()
for i := 0; i < length; i++ {
node := queue.Remove(queue.Front()).(*TreeNode)
if node.Left != nil {
queue.PushBack(node.Left)
}
if node.Right != nil {
queue.PushBack(node.Right)
}
// 取每层的最后一个元素,添加到结果集中
if i == length-1 {
res = append(res, node.Val)
}
}
}
return res
}// 使用切片作为队列
func rightSideView(root *TreeNode) []int {
res := make([]int, 0)
if root == nil {
return res
}
queue := make([]*TreeNode, 0)
queue = append(queue, root)
for len(queue) > 0 {
size := len(queue)
for i := 0; i < size; i++ {
node := queue[0]
queue = queue[1:]
if node.Left != nil {
queue = append(queue, node.Left)
}
if node.Right != nil {
queue = append(queue, node.Right)
}
if i == size-1 {
res = append(res, node.Val)
}
}
}
return res
}var rightSideView = function(root) {
//二叉树右视图 只需要把每一层最后一个节点存储到res数组
let res = [], queue = [];
queue.push(root);
while(queue.length && root!==null) {
// 记录当前层级节点个数
let length = queue.length;
while(length--) {
let node = queue.shift();
// length长度为0的时候表明到了层级最后一个节点
if(!length) {
res.push(node.val);
}
node.left && queue.push(node.left);
node.right && queue.push(node.right);
}
}
return res;
};function rightSideView(root: TreeNode | null): number[] {
let helperQueue: TreeNode[] = [];
let resArr: number[] = [];
let tempNode: TreeNode;
if (root !== null) helperQueue.push(root);
while (helperQueue.length > 0) {
for (let i = 0, length = helperQueue.length; i < length; i++) {
tempNode = helperQueue.shift()!;
if (i === length - 1) resArr.push(tempNode.val);
if (tempNode.left !== null) helperQueue.push(tempNode.left);
if (tempNode.right !== null) helperQueue.push(tempNode.right);
}
}
return resArr;
};func rightSideView(_ root: TreeNode?) -> [Int] {
// 表示一层
var queue = [TreeNode]()
if let node = root { queue.append(node) }
var result = [Int]()
while !queue.isEmpty {
let count = queue.count
for i in 0 ..< count {
// 当前层
let node = queue.removeFirst()
if i == count - 1 { result.append(node.val) }
// 下一层
if let node = node.left { queue.append(node) }
if let node = node.right { queue.append(node) }
}
}
return result
}// 199.二叉树的右视图
object Solution {
import scala.collection.mutable
def rightSideView(root: TreeNode): List[Int] = {
val res = mutable.ListBuffer[Int]()
if (root == null) return res.toList
val queue = mutable.Queue[TreeNode]()
queue.enqueue(root)
while (!queue.isEmpty) {
val len = queue.size
var curNode: TreeNode = null
for (i <- 0 until len) {
curNode = queue.dequeue()
if (curNode.left != null) queue.enqueue(curNode.left)
if (curNode.right != null) queue.enqueue(curNode.right)
}
res.append(curNode.value) // 把最后一个节点的值加入解集
}
res.toList // 最后需要把res转换为List,return关键字可以省略
}
}use std::cell::RefCell;
use std::collections::VecDeque;
use std::rc::Rc;
impl Solution {
pub fn right_side_view(root: Option<Rc<RefCell<TreeNode>>>) -> Vec<i32> {
let mut res = vec![];
let mut queue = VecDeque::new();
if root.is_some() {
queue.push_back(root);
}
while !queue.is_empty() {
let len = queue.len();
for i in 0..len {
let node = queue.pop_front().unwrap().unwrap();
if i == len - 1 {
res.push(node.borrow().val);
}
if node.borrow().left.is_some() {
queue.push_back(node.borrow().left.clone());
}
if node.borrow().right.is_some() {
queue.push_back(node.borrow().right.clone());
}
}
}
res
}
}给定一个非空二叉树, 返回一个由每层节点平均值组成的数组。
本题就是层序遍历的时候把一层求个总和再取一个均值。
C++代码:
class Solution {
public:
vector<double> averageOfLevels(TreeNode* root) {
queue<TreeNode*> que;
if (root != NULL) que.push(root);
vector<double> result;
while (!que.empty()) {
int size = que.size();
double sum = 0; // 统计每一层的和
for (int i = 0; i < size; i++) {
TreeNode* node = que.front();
que.pop();
sum += node->val;
if (node->left) que.push(node->left);
if (node->right) que.push(node->right);
}
result.push_back(sum / size); // 将每一层均值放进结果集
}
return result;
}
};
class Solution:
"""二叉树层平均值迭代解法"""
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def averageOfLevels(self, root: TreeNode) -> List[float]:
if not root:
return []
queue = collections.deque([root])
averages = []
while queue:
size = len(queue)
level_sum = 0
for i in range(size):
node = queue.popleft()
level_sum += node.val
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
averages.append(level_sum / size)
return averages// 637. 二叉树的层平均值
public class N0637 {
/**
* 解法:队列,迭代。
* 每次返回每层的最后一个字段即可。
*/
public List<Double> averageOfLevels(TreeNode root) {
List<Double> list = new ArrayList<>();
Deque<TreeNode> que = new LinkedList<>();
if (root == null) {
return list;
}
que.offerLast(root);
while (!que.isEmpty()) {
int levelSize = que.size();
double levelSum = 0.0;
for (int i = 0; i < levelSize; i++) {
TreeNode poll = que.pollFirst();
levelSum += poll.val;
if (poll.left != null) {
que.addLast(poll.left);
}
if (poll.right != null) {
que.addLast(poll.right);
}
}
list.add(levelSum / levelSize);
}
return list;
}
}/**
637. 二叉树的层平均值
*/
func averageOfLevels(root *TreeNode) []float64 {
if root == nil {
// 防止为空
return nil
}
res := make([]float64, 0)
queue := list.New()
queue.PushBack(root)
var sum int
for queue.Len() > 0 {
//保存当前层的长度,然后处理当前层(十分重要,防止添加下层元素影响判断层中元素的个数)
length := queue.Len()
for i := 0; i < length; i++ {
node := queue.Remove(queue.Front()).(*TreeNode)
if node.Left != nil {
queue.PushBack(node.Left)
}
if node.Right != nil {
queue.PushBack(node.Right)
}
// 当前层元素求和
sum += node.Val
}
// 计算每层的平均值,将结果添加到响应结果中
res = append(res, float64(sum)/float64(length))
sum = 0 // 清空该层的数据
}
return res
}// 使用切片作为队列
func averageOfLevels(root *TreeNode) []float64 {
res := make([]float64, 0)
if root == nil {
return res
}
queue := make([]*TreeNode, 0)
queue = append(queue, root)
for len(queue) > 0 {
size := len(queue)
sum := 0
for i := 0; i < size; i++ {
node := queue[0]
queue = queue[1:]
sum += node.Val
if node.Left != nil {
queue = append(queue, node.Left)
}
if node.Right != nil {
queue = append(queue, node.Right)
}
}
res = append(res, float64(sum)/float64(size))
}
return res
}var averageOfLevels = function(root) {
let res = [],
queue = [];
queue.push(root);
while (queue.length) {
// 每一层节点个数;
let lengthLevel = queue.length,
len = queue.length,
// sum记录每一层的和;
sum = 0;
while (lengthLevel--) {
const node = queue.shift();
sum += node.val;
// 队列存放下一层节点
node.left && queue.push(node.left);
node.right && queue.push(node.right);
}
// 求平均值
res.push(sum / len);
}
return res;
};function averageOfLevels(root: TreeNode | null): number[] {
let helperQueue: TreeNode[] = [];
let resArr: number[] = [];
let total: number = 0;
let tempNode: TreeNode;
if (root !== null) helperQueue.push(root);
while (helperQueue.length > 0) {
let length = helperQueue.length;
for (let i = 0; i < length; i++) {
tempNode = helperQueue.shift()!;
total += tempNode.val;
if (tempNode.left) helperQueue.push(tempNode.left);
if (tempNode.right) helperQueue.push(tempNode.right);
}
resArr.push(total / length);
total = 0;
}
return resArr;
};func averageOfLevels(_ root: TreeNode?) -> [Double] {
// 表示一层
var queue = [TreeNode]()
if let node = root { queue.append(node) }
var result = [Double]()
while !queue.isEmpty {
let count = queue.count
var sum = 0
for _ in 0 ..< count {
// 当前层
let node = queue.removeFirst()
sum += node.val
// 下一层
if let node = node.left { queue.append(node) }
if let node = node.right { queue.append(node) }
}
result.append(Double(sum) / Double(count))
}
return result
}// 637.二叉树的层平均值
object Solution {
import scala.collection.mutable
def averageOfLevels(root: TreeNode): Array[Double] = {
val res = mutable.ArrayBuffer[Double]()
val queue = mutable.Queue[TreeNode]()
queue.enqueue(root)
while (!queue.isEmpty) {
var sum = 0.0
var len = queue.size
for (i <- 0 until len) {
var curNode = queue.dequeue()
sum += curNode.value // 累加该层的值
if (curNode.left != null) queue.enqueue(curNode.left)
if (curNode.right != null) queue.enqueue(curNode.right)
}
res.append(sum / len) // 平均值即为sum/len
}
res.toArray // 最后需要转换为Array,return关键字可以省略
}
}use std::cell::RefCell;
use std::collections::VecDeque;
use std::rc::Rc;
impl Solution {
pub fn average_of_levels(root: Option<Rc<RefCell<TreeNode>>>) -> Vec<f64> {
let mut res = vec![];
let mut queue = VecDeque::new();
if root.is_some() {
queue.push_back(root);
}
while !queue.is_empty() {
let len = queue.len();
let mut sum = 0;
for _ in 0..len {
let node = queue.pop_front().unwrap().unwrap();
sum += node.borrow().val;
if node.borrow().left.is_some() {
queue.push_back(node.borrow().left.clone());
}
if node.borrow().right.is_some() {
queue.push_back(node.borrow().right.clone());
}
}
res.push((sum as f64) / len as f64);
}
res
}
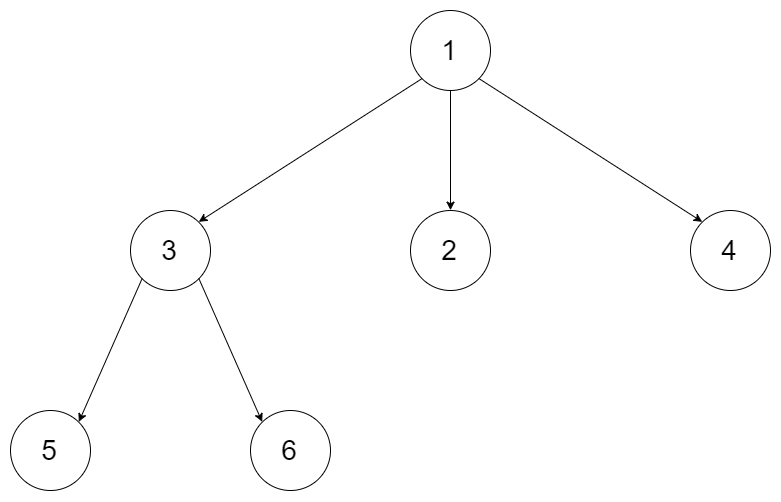
}给定一个 N 叉树,返回其节点值的层序遍历。 (即从左到右,逐层遍历)。
例如,给定一个 3叉树 :
返回其层序遍历:
[ [1], [3,2,4], [5,6] ]
这道题依旧是模板题,只不过一个节点有多个孩子了
C++代码:
class Solution {
public:
vector<vector<int>> levelOrder(Node* root) {
queue<Node*> que;
if (root != NULL) que.push(root);
vector<vector<int>> result;
while (!que.empty()) {
int size = que.size();
vector<int> vec;
for (int i = 0; i < size; i++) {
Node* node = que.front();
que.pop();
vec.push_back(node->val);
for (int i = 0; i < node->children.size(); i++) { // 将节点孩子加入队列
if (node->children[i]) que.push(node->children[i]);
}
}
result.push_back(vec);
}
return result;
}
};"""
# Definition for a Node.
class Node:
def __init__(self, val=None, children=None):
self.val = val
self.children = children
"""
class Solution:
def levelOrder(self, root: 'Node') -> List[List[int]]:
if not root:
return []
result = []
queue = collections.deque([root])
while queue:
level_size = len(queue)
level = []
for _ in range(level_size):
node = queue.popleft()
level.append(node.val)
for child in node.children:
queue.append(child)
result.append(level)
return result# LeetCode 429. N-ary Tree Level Order Traversal
# 递归法
class Solution:
def levelOrder(self, root: 'Node') -> List[List[int]]:
if not root: return []
result=[]
def traversal(root,depth):
if len(result)==depth:result.append([])
result[depth].append(root.val)
if root.children:
for i in range(len(root.children)):traversal(root.children[i],depth+1)
traversal(root,0)
return result// 429. N 叉树的层序遍历
public class N0429 {
/**
* 解法1:队列,迭代。
*/
public List<List<Integer>> levelOrder(Node root) {
List<List<Integer>> list = new ArrayList<>();
Deque<Node> que = new LinkedList<>();
if (root == null) {
return list;
}
que.offerLast(root);
while (!que.isEmpty()) {
int levelSize = que.size();
List<Integer> levelList = new ArrayList<>();
for (int i = 0; i < levelSize; i++) {
Node poll = que.pollFirst();
levelList.add(poll.val);
List<Node> children = poll.children;
if (children == null || children.size() == 0) {
continue;
}
for (Node child : children) {
if (child != null) {
que.offerLast(child);
}
}
}
list.add(levelList);
}
return list;
}
class Node {
public int val;
public List<Node> children;
public Node() {}
public Node(int _val) {
val = _val;
}
public Node(int _val, List<Node> _children) {
val = _val;
children = _children;
}
}
}/**
429. N 叉树的层序遍历
*/
func levelOrder(root *Node) [][]int {
queue := list.New()
res := [][]int{} //结果集
if root == nil{
return res
}
queue.PushBack(root)
for queue.Len() > 0 {
length := queue.Len() //记录当前层的数量
var tmp []int
for T := 0; T < length; T++ { //该层的每个元素:一添加到该层的结果集中;二找到该元素的下层元素加入到队列中,方便下次使用
myNode := queue.Remove(queue.Front()).(*Node)
tmp = append(tmp, myNode.Val)
for i := 0; i < len(myNode.Children); i++ {
queue.PushBack(myNode.Children[i])
}
}
res = append(res, tmp)
}
return res
}// 使用切片作为队列
func levelOrder(root *Node) [][]int {
res := make([][]int, 0)
if root == nil {
return res
}
queue := make([]*Node, 0)
queue = append(queue, root)
for len(queue) > 0 {
size := len(queue)
level := make([]int, 0)
for i := 0; i < size; i++ {
node := queue[0]
queue = queue[1:]
level = append(level, node.Val)
if len(node.Children) > 0 {
queue = append(queue, node.Children...)
}
}
res = append(res, level)
}
return res
}var levelOrder = function(root) {
//每一层可能有2个以上,所以不再使用node.left node.right
let res = [], queue = [];
queue.push(root);
while(queue.length && root!==null) {
//记录每一层节点个数还是和二叉树一致
let length = queue.length;
//存放每层节点 也和二叉树一致
let curLevel = [];
while(length--) {
let node = queue.shift();
curLevel.push(node.val);
//这里不再是 ndoe.left node.right 而是循坏node.children
for(let item of node.children){
item && queue.push(item);
}
}
res.push(curLevel);
}
return res;
};function levelOrder(root: Node | null): number[][] {
let helperQueue: Node[] = [];
let resArr: number[][] = [];
let tempArr: number[] = [];
if (root !== null) helperQueue.push(root);
let curNode: Node;
while (helperQueue.length > 0) {
for (let i = 0, length = helperQueue.length; i < length; i++) {
curNode = helperQueue.shift()!;
tempArr.push(curNode.val);
helperQueue.push(...curNode.children);
}
resArr.push(tempArr);
tempArr = [];
}
return resArr;
};func levelOrder(_ root: Node?) -> [[Int]] {
// 表示一层
var queue = [Node]()
if let node = root { queue.append(node) }
var result = [[Int]]()
while !queue.isEmpty {
let count = queue.count
var subarray = [Int]()
for _ in 0 ..< count {
// 当前层
let node = queue.removeFirst()
subarray.append(node.val)
// 下一层
for node in node.children { queue.append(node) }
}
result.append(subarray)
}
return result
}// 429.N叉树的层序遍历
object Solution {
import scala.collection.mutable
def levelOrder(root: Node): List[List[Int]] = {
val res = mutable.ListBuffer[List[Int]]()
if (root == null) return res.toList
val queue = mutable.Queue[Node]()
queue.enqueue(root) // 根节点入队
while (!queue.isEmpty) {
val tmp = mutable.ListBuffer[Int]() // 存储每层节点
val len = queue.size
for (i <- 0 until len) {
val curNode = queue.dequeue()
tmp.append(curNode.value) // 将该节点的值加入tmp
// 循环遍历该节点的子节点,加入队列
for (child <- curNode.children) {
queue.enqueue(child)
}
}
res.append(tmp.toList) // 将该层的节点放到结果集
}
res.toList
}
}pub struct Solution;
#[derive(Debug, PartialEq, Eq)]
pub struct Node {
pub val: i32,
pub children: Vec<Option<Rc<RefCell<Node>>>>,
}
impl Node {
#[inline]
pub fn new(val: i32) -> Node {
Node {
val,
children: vec![],
}
}
}
use std::cell::RefCell;
use std::collections::VecDeque;
use std::rc::Rc;
impl Solution {
pub fn level_order(root: Option<Rc<RefCell<Node>>>) -> Vec<Vec<i32>> {
let mut res = vec![];
let mut queue = VecDeque::new();
if root.is_some() {
queue.push_back(root);
}
while !queue.is_empty() {
let mut temp = vec![];
for _ in 0..queue.len() {
let node = queue.pop_front().unwrap().unwrap();
temp.push(node.borrow().val);
if !node.borrow().children.is_empty() {
for n in node.borrow().children.clone() {
queue.push_back(n);
}
}
}
res.push(temp)
}
res
}
}您需要在二叉树的每一行中找到最大的值。
层序遍历,取每一层的最大值
C++代码:
class Solution {
public:
vector<int> largestValues(TreeNode* root) {
queue<TreeNode*> que;
if (root != NULL) que.push(root);
vector<int> result;
while (!que.empty()) {
int size = que.size();
int maxValue = INT_MIN; // 取每一层的最大值
for (int i = 0; i < size; i++) {
TreeNode* node = que.front();
que.pop();
maxValue = node->val > maxValue ? node->val : maxValue;
if (node->left) que.push(node->left);
if (node->right) que.push(node->right);
}
result.push_back(maxValue); // 把最大值放进数组
}
return result;
}
};# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def largestValues(self, root: TreeNode) -> List[int]:
if not root:
return []
result = []
queue = collections.deque([root])
while queue:
level_size = len(queue)
max_val = float('-inf')
for _ in range(level_size):
node = queue.popleft()
max_val = max(max_val, node.val)
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
result.append(max_val)
return resultclass Solution {
public List<Integer> largestValues(TreeNode root) {
if(root == null){
return Collections.emptyList();
}
List<Integer> result = new ArrayList();
Queue<TreeNode> queue = new LinkedList();
queue.offer(root);
while(!queue.isEmpty()){
int max = Integer.MIN_VALUE;
for(int i = queue.size(); i > 0; i--){
TreeNode node = queue.poll();
max = Math.max(max, node.val);
if(node.left != null) queue.offer(node.left);
if(node.right != null) queue.offer(node.right);
}
result.add(max);
}
return result;
}
}/**
515. 在每个树行中找最大值
*/
func largestValues(root *TreeNode) []int {
if root == nil {
//防止为空
return nil
}
queue := list.New()
queue.PushBack(root)
ans := make([]int, 0)
temp := math.MinInt64
// 层序遍历
for queue.Len() > 0 {
//保存当前层的长度,然后处理当前层(十分重要,防止添加下层元素影响判断层中元素的个数)
length := queue.Len()
for i := 0; i < length; i++ {
node := queue.Remove(queue.Front()).(*TreeNode)//出队列
// 比较当前层中的最大值和新遍历的元素大小,取两者中大值
temp = max(temp, node.Val)
if node.Left != nil {
queue.PushBack(node.Left)
}
if node.Right != nil {
queue.PushBack(node.Right)
}
}
ans = append(ans, temp)
temp = math.MinInt64
}
return ans
}
func max(x, y int) int {
if x > y {
return x
}
return y
}// 使用切片作为队列
func largestValues(root *TreeNode) []int {
res := make([]int, 0)
if root == nil {
return res
}
queue := make([]*TreeNode, 0)
queue = append(queue, root)
for len(queue) > 0 {
size := len(queue)
maxValue := math.MinInt64
for i := 0; i < size; i++ {
node := queue[0]
queue = queue[1:]
if node.Val > maxValue {
maxValue = node.Val
}
if node.Left != nil {
queue = append(queue, node.Left)
}
if node.Right != nil {
queue = append(queue, node.Right)
}
}
res = append(res, maxValue)
}
return res
}var largestValues = function (root) {
let res = [],
queue = [];
queue.push(root);
if (root === null) {
return res;
}
while (queue.length) {
let lengthLevel = queue.length,
// 初始值设为负无穷大
max = -Infinity;
while (lengthLevel--) {
const node = queue.shift();
// 在当前层中找到最大值
max = Math.max(max, node.val);
// 找到下一层的节点
node.left && queue.push(node.left);
node.right && queue.push(node.right);
}
res.push(max);
}
return res;
};function largestValues(root: TreeNode | null): number[] {
let helperQueue: TreeNode[] = [];
let resArr: number[] = [];
let tempNode: TreeNode;
let max: number = 0;
if (root !== null) helperQueue.push(root);
while (helperQueue.length > 0) {
for (let i = 0, length = helperQueue.length; i < length; i++) {
tempNode = helperQueue.shift()!;
if (i === 0) {
max = tempNode.val;
} else {
max = max > tempNode.val ? max : tempNode.val;
}
if (tempNode.left) helperQueue.push(tempNode.left);
if (tempNode.right) helperQueue.push(tempNode.right);
}
resArr.push(max);
}
return resArr;
};func largestValues(_ root: TreeNode?) -> [Int] {
// 表示一层
var queue = [TreeNode]()
if let node = root { queue.append(node) }
var result = [Int]()
while !queue.isEmpty {
let count = queue.count
var max = queue[0].val
for _ in 0 ..< count {
// 当前层
let node = queue.removeFirst()
if node.val > max { max = node.val }
// 下一层
if let node = node.left { queue.append(node) }
if let node = node.right { queue.append(node) }
}
result.append(max)
}
return result
}// 515.在每个树行中找最大值
object Solution {
import scala.collection.mutable
def largestValues(root: TreeNode): List[Int] = {
val res = mutable.ListBuffer[Int]()
if (root == null) return res.toList
val queue = mutable.Queue[TreeNode]()
queue.enqueue(root)
while (!queue.isEmpty) {
var max = Int.MinValue // 初始化max为系统最小值
val len = queue.size
for (i <- 0 until len) {
val curNode = queue.dequeue()
max = math.max(max, curNode.value) // 对比求解最大值
if (curNode.left != null) queue.enqueue(curNode.left)
if (curNode.right != null) queue.enqueue(curNode.right)
}
res.append(max) // 将最大值放入结果集
}
res.toList
}
}use std::cell::RefCell;
use std::collections::VecDeque;
use std::rc::Rc;
impl Solution {
pub fn largest_values(root: Option<Rc<RefCell<TreeNode>>>) -> Vec<i32> {
let mut res = vec![];
let mut queue = VecDeque::new();
if root.is_some() {
queue.push_back(root);
}
while !queue.is_empty() {
let mut max = i32::MIN;
for _ in 0..queue.len() {
let node = queue.pop_front().unwrap().unwrap();
max = max.max(node.borrow().val);
if node.borrow().left.is_some() {
queue.push_back(node.borrow().left.clone());
}
if node.borrow().right.is_some() {
queue.push_back(node.borrow().right.clone());
}
}
res.push(max);
}
res
}
}给定一个完美二叉树,其所有叶子节点都在同一层,每个父节点都有两个子节点。二叉树定义如下:
struct Node {
int val;
Node *left;
Node *right;
Node *next;
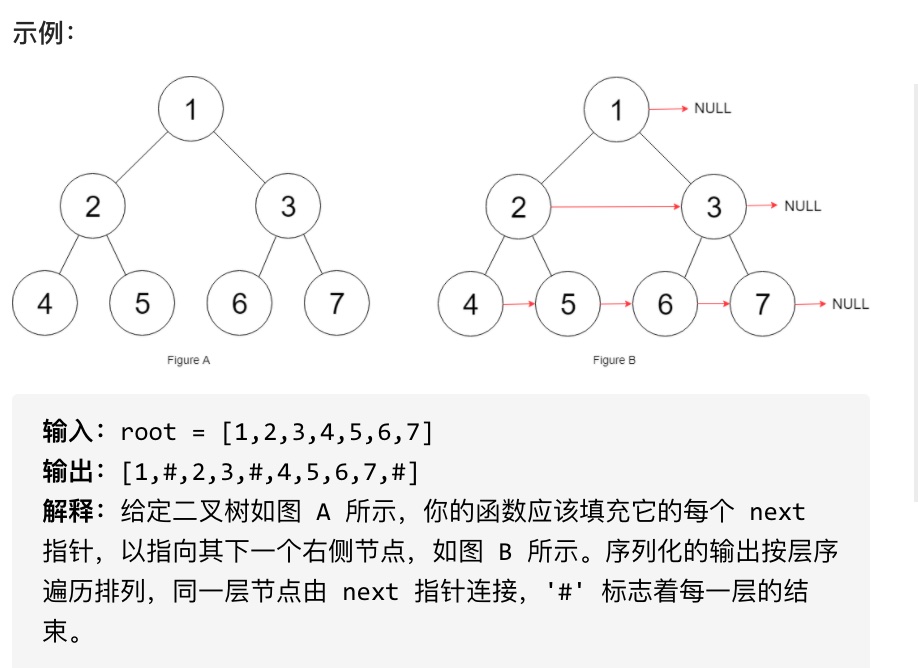
}填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL。
初始状态下,所有 next 指针都被设置为 NULL。
本题依然是层序遍历,只不过在单层遍历的时候记录一下本层的头部节点,然后在遍历的时候让前一个节点指向本节点就可以了
C++代码:
class Solution {
public:
Node* connect(Node* root) {
queue<Node*> que;
if (root != NULL) que.push(root);
while (!que.empty()) {
int size = que.size();
// vector<int> vec;
Node* nodePre;
Node* node;
for (int i = 0; i < size; i++) {
if (i == 0) {
nodePre = que.front(); // 取出一层的头结点
que.pop();
node = nodePre;
} else {
node = que.front();
que.pop();
nodePre->next = node; // 本层前一个节点next指向本节点
nodePre = nodePre->next;
}
if (node->left) que.push(node->left);
if (node->right) que.push(node->right);
}
nodePre->next = NULL; // 本层最后一个节点指向NULL
}
return root;
}
};class Solution {
public Node connect(Node root) {
Queue<Node> tmpQueue = new LinkedList<Node>();
if (root != null) tmpQueue.add(root);
while (tmpQueue.size() != 0){
int size = tmpQueue.size();
Node cur = tmpQueue.poll();
if (cur.left != null) tmpQueue.add(cur.left);
if (cur.right != null) tmpQueue.add(cur.right);
for (int index = 1; index < size; index++){
Node next = tmpQueue.poll();
if (next.left != null) tmpQueue.add(next.left);
if (next.right != null) tmpQueue.add(next.right);
cur.next = next;
cur = next;
}
}
return root;
}
}"""
# Definition for a Node.
class Node:
def __init__(self, val: int = 0, left: 'Node' = None, right: 'Node' = None, next: 'Node' = None):
self.val = val
self.left = left
self.right = right
self.next = next
"""
class Solution:
def connect(self, root: 'Node') -> 'Node':
if not root:
return root
queue = collections.deque([root])
while queue:
level_size = len(queue)
prev = None
for i in range(level_size):
node = queue.popleft()
if prev:
prev.next = node
prev = node
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
return root/**
116. 填充每个节点的下一个右侧节点指针
117. 填充每个节点的下一个右侧节点指针 II
*/
func connect(root *Node) *Node {
if root == nil { //防止为空
return root
}
queue := list.New()
queue.PushBack(root)
tmpArr := make([]*Node, 0)
for queue.Len() > 0 {
length := queue.Len() //保存当前层的长度,然后处理当前层(十分重要,防止添加下层元素影响判断层中元素的个数)
for i := 0; i < length; i++ {
node := queue.Remove(queue.Front()).(*Node) //出队列
if node.Left != nil {
queue.PushBack(node.Left)
}
if node.Right != nil {
queue.PushBack(node.Right)
}
tmpArr = append(tmpArr, node) //将值加入本层切片中
}
if len(tmpArr) > 1 {
// 遍历每层元素,指定next
for i := 0; i < len(tmpArr)-1; i++ {
tmpArr[i].Next = tmpArr[i+1]
}
}
tmpArr = []*Node{} //清空层的数据
}
return root
}// 使用切片作为队列
func connect(root *Node) *Node {
if root == nil {
return root
}
queue := make([]*Node, 0)
queue = append(queue, root)
for len(queue) > 0 {
size := len(queue)
for i := 0; i < size; i++ {
node := queue[i]
if i != size - 1 {
queue[i].Next = queue[i+1]
}
if node.Left != nil {
queue = append(queue, node.Left)
}
if node.Right != nil {
queue = append(queue, node.Right)
}
}
queue = queue[size:]
}
return root
}/**
* // Definition for a Node.
* function Node(val, left, right, next) {
* this.val = val === undefined ? null : val;
* this.left = left === undefined ? null : left;
* this.right = right === undefined ? null : right;
* this.next = next === undefined ? null : next;
* };
*/
/**
* @param {Node} root
* @return {Node}
*/
var connect = function(root) {
if (root === null) return root;
let queue = [root];
while (queue.length) {
let n = queue.length;
for (let i = 0; i < n; i++) {
let node = queue.shift();
if (i < n-1) {
node.next = queue[0];
}
node.left && queue.push(node.left);
node.right && queue.push(node.right);
}
}
return root;
};function connect(root: Node | null): Node | null {
let helperQueue: Node[] = [];
let preNode: Node, curNode: Node;
if (root !== null) helperQueue.push(root);
while (helperQueue.length > 0) {
for (let i = 0, length = helperQueue.length; i < length; i++) {
if (i === 0) {
preNode = helperQueue.shift()!;
} else {
curNode = helperQueue.shift()!;
preNode.next = curNode;
preNode = curNode;
}
if (preNode.left) helperQueue.push(preNode.left);
if (preNode.right) helperQueue.push(preNode.right);
}
preNode.next = null;
}
return root;
};func connect(_ root: Node?) -> Node? {
// 表示一层
var queue = [Node]()
if let node = root { queue.append(node) }
while !queue.isEmpty {
let count = queue.count
var current, previous: Node!
for i in 0 ..< count {
// 当前层
if i == 0 {
previous = queue.removeFirst()
current = previous
} else {
current = queue.removeFirst()
previous.next = current
previous = current
}
// 下一层
if let node = current.left { queue.append(node) }
if let node = current.right { queue.append(node) }
}
previous.next = nil
}
return root
}// 116.填充每个节点的下一个右侧节点指针
object Solution {
import scala.collection.mutable
def connect(root: Node): Node = {
if (root == null) return root
val queue = mutable.Queue[Node]()
queue.enqueue(root)
while (!queue.isEmpty) {
val len = queue.size
val tmp = mutable.ListBuffer[Node]()
for (i <- 0 until len) {
val curNode = queue.dequeue()
tmp.append(curNode)
if (curNode.left != null) queue.enqueue(curNode.left)
if (curNode.right != null) queue.enqueue(curNode.right)
}
// 处理next指针
for (i <- 0 until tmp.size - 1) {
tmp(i).next = tmp(i + 1)
}
tmp(tmp.size-1).next = null
}
root
}
}这道题目说是二叉树,但116题目说是完整二叉树,其实没有任何差别,一样的代码一样的逻辑一样的味道
C++代码:
class Solution {
public:
Node* connect(Node* root) {
queue<Node*> que;
if (root != NULL) que.push(root);
while (!que.empty()) {
int size = que.size();
vector<int> vec;
Node* nodePre;
Node* node;
for (int i = 0; i < size; i++) {
if (i == 0) {
nodePre = que.front(); // 取出一层的头结点
que.pop();
node = nodePre;
} else {
node = que.front();
que.pop();
nodePre->next = node; // 本层前一个节点next指向本节点
nodePre = nodePre->next;
}
if (node->left) que.push(node->left);
if (node->right) que.push(node->right);
}
nodePre->next = NULL; // 本层最后一个节点指向NULL
}
return root;
}
};// 二叉树之层次遍历
class Solution {
public Node connect(Node root) {
Queue<Node> queue = new LinkedList<>();
if (root != null) {
queue.add(root);
}
while (!queue.isEmpty()) {
int size = queue.size();
Node node = null;
Node nodePre = null;
for (int i = 0; i < size; i++) {
if (i == 0) {
nodePre = queue.poll(); // 取出本层头一个节点
node = nodePre;
} else {
node = queue.poll();
nodePre.next = node; // 本层前一个节点 next 指向当前节点
nodePre = nodePre.next;
}
if (node.left != null) {
queue.add(node.left);
}
if (node.right != null) {
queue.add(node.right);
}
}
nodePre.next = null; // 本层最后一个节点 next 指向 null
}
return root;
}
}# 层序遍历解法
"""
# Definition for a Node.
class Node:
def __init__(self, val: int = 0, left: 'Node' = None, right: 'Node' = None, next: 'Node' = None):
self.val = val
self.left = left
self.right = right
self.next = next
"""
class Solution:
def connect(self, root: 'Node') -> 'Node':
if not root:
return root
queue = collections.deque([root])
while queue:
level_size = len(queue)
prev = None
for i in range(level_size):
node = queue.popleft()
if prev:
prev.next = node
prev = node
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
return root/**
116. 填充每个节点的下一个右侧节点指针
117. 填充每个节点的下一个右侧节点指针 II
*/
func connect(root *Node) *Node {
if root == nil { //防止为空
return root
}
queue := list.New()
queue.PushBack(root)
tmpArr := make([]*Node, 0)
for queue.Len() > 0 {
length := queue.Len() //保存当前层的长度,然后处理当前层(十分重要,防止添加下层元素影响判断层中元素的个数)
for i := 0; i < length; i++ {
node := queue.Remove(queue.Front()).(*Node) //出队列
if node.Left != nil {
queue.PushBack(node.Left)
}
if node.Right != nil {
queue.PushBack(node.Right)
}
tmpArr = append(tmpArr, node) //将值加入本层切片中
}
if len(tmpArr) > 1 {
// 遍历每层元素,指定next
for i := 0; i < len(tmpArr)-1; i++ {
tmpArr[i].Next = tmpArr[i+1]
}
}
tmpArr = []*Node{} //清空层的数据
}
return root
}// 使用切片作为队列
func connect(root *Node) *Node {
if root == nil {
return root
}
queue := make([]*Node, 0)
queue = append(queue, root)
for len(queue) > 0 {
size := len(queue)
for i := 0; i < size; i++ {
node := queue[i]
if i != size - 1 {
queue[i].Next = queue[i+1]
}
if node.Left != nil {
queue = append(queue, node.Left)
}
if node.Right != nil {
queue = append(queue, node.Right)
}
}
queue = queue[size:]
}
return root
}/**
* // Definition for a Node.
* function Node(val, left, right, next) {
* this.val = val === undefined ? null : val;
* this.left = left === undefined ? null : left;
* this.right = right === undefined ? null : right;
* this.next = next === undefined ? null : next;
* };
*/
/**
* @param {Node} root
* @return {Node}
*/
var connect = function(root) {
if (root === null) {
return null;
}
let queue = [root];
while (queue.length > 0) {
let n = queue.length;
for (let i=0; i<n; i++) {
let node = queue.shift();
if (i < n-1) node.next = queue[0];
if (node.left != null) queue.push(node.left);
if (node.right != null) queue.push(node.right);
}
}
return root;
};function connect(root: Node | null): Node | null {
let helperQueue: Node[] = [];
let preNode: Node, curNode: Node;
if (root !== null) helperQueue.push(root);
while (helperQueue.length > 0) {
for (let i = 0, length = helperQueue.length; i < length; i++) {
if (i === 0) {
preNode = helperQueue.shift()!;
} else {
curNode = helperQueue.shift()!;
preNode.next = curNode;
preNode = curNode;
}
if (preNode.left) helperQueue.push(preNode.left);
if (preNode.right) helperQueue.push(preNode.right);
}
preNode.next = null;
}
return root;
};func connect(_ root: Node?) -> Node? {
// 表示一层
var queue = [Node]()
if let node = root { queue.append(node) }
while !queue.isEmpty {
let count = queue.count
var current, previous: Node!
for i in 0 ..< count {
// 当前层
if i == 0 {
previous = queue.removeFirst()
current = previous
} else {
current = queue.removeFirst()
previous.next = current
previous = current
}
// 下一层
if let node = current.left { queue.append(node) }
if let node = current.right { queue.append(node) }
}
previous.next = nil
}
return root
}// 117.填充每个节点的下一个右侧节点指针II
object Solution {
import scala.collection.mutable
def connect(root: Node): Node = {
if (root == null) return root
val queue = mutable.Queue[Node]()
queue.enqueue(root)
while (!queue.isEmpty) {
val len = queue.size
val tmp = mutable.ListBuffer[Node]()
for (i <- 0 until len) {
val curNode = queue.dequeue()
tmp.append(curNode)
if (curNode.left != null) queue.enqueue(curNode.left)
if (curNode.right != null) queue.enqueue(curNode.right)
}
// 处理next指针
for (i <- 0 until tmp.size - 1) {
tmp(i).next = tmp(i + 1)
}
tmp(tmp.size-1).next = null
}
root
}
}给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例:
给定二叉树 [3,9,20,null,null,15,7],
返回它的最大深度 3 。
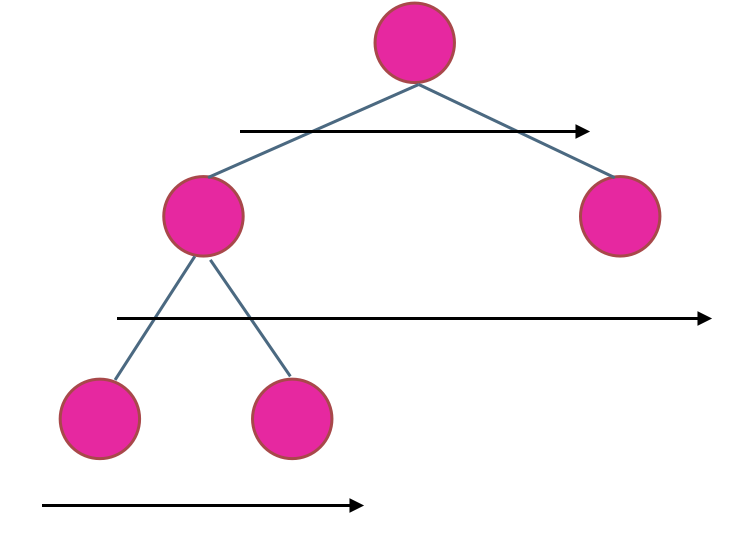
使用迭代法的话,使用层序遍历是最为合适的,因为最大的深度就是二叉树的层数,和层序遍历的方式极其吻合。
在二叉树中,一层一层的来遍历二叉树,记录一下遍历的层数就是二叉树的深度,如图所示:
所以这道题的迭代法就是一道模板题,可以使用二叉树层序遍历的模板来解决的。
C++代码如下:
class Solution {
public:
int maxDepth(TreeNode* root) {
if (root == NULL) return 0;
int depth = 0;
queue<TreeNode*> que;
que.push(root);
while(!que.empty()) {
int size = que.size();
depth++; // 记录深度
for (int i = 0; i < size; i++) {
TreeNode* node = que.front();
que.pop();
if (node->left) que.push(node->left);
if (node->right) que.push(node->right);
}
}
return depth;
}
};class Solution {
public int maxDepth(TreeNode root) {
if (root == null) return 0;
Queue<TreeNode> que = new LinkedList<>();
que.offer(root);
int depth = 0;
while (!que.isEmpty())
{
int len = que.size();
while (len > 0)
{
TreeNode node = que.poll();
if (node.left != null) que.offer(node.left);
if (node.right != null) que.offer(node.right);
len--;
}
depth++;
}
return depth;
}
}# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def maxDepth(self, root: TreeNode) -> int:
if not root:
return 0
depth = 0
queue = collections.deque([root])
while queue:
depth += 1
for _ in range(len(queue)):
node = queue.popleft()
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
return depth/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func maxDepth(root *TreeNode) int {
ans := 0
if root == nil {
return 0
}
queue := list.New()
queue.PushBack(root)
for queue.Len() > 0 {
length := queue.Len()
for i := 0; i < length; i++ {
node := queue.Remove(queue.Front()).(*TreeNode)
if node.Left != nil {
queue.PushBack(node.Left)
}
if node.Right != nil {
queue.PushBack(node.Right)
}
}
ans++//记录深度,其他的是层序遍历的板子
}
return ans
}// 使用切片作为队列
func maxDepth(root *TreeNode) int {
if root == nil {
return 0
}
depth := 0
queue := make([]*TreeNode, 0)
queue = append(queue, root)
for len(queue) > 0 {
size := len(queue)
for i := 0; i < size; i++ {
node := queue[0]
queue = queue[1:]
if node.Left != nil {
queue = append(queue, node.Left)
}
if node.Right != nil {
queue = append(queue, node.Right)
}
}
depth++
}
return depth
}/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number}
*/
var maxDepth = function (root) {
// 二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
let max = 0,
queue = [root];
if (root === null) {
return max;
}
while (queue.length) {
max++;
let length = queue.length;
while (length--) {
let node = queue.shift();
node.left && queue.push(node.left);
node.right && queue.push(node.right);
}
}
return max;
};function maxDepth(root: TreeNode | null): number {
let helperQueue: TreeNode[] = [];
let resDepth: number = 0;
let tempNode: TreeNode;
if (root !== null) helperQueue.push(root);
while (helperQueue.length > 0) {
resDepth++;
for (let i = 0, length = helperQueue.length; i < length; i++) {
tempNode = helperQueue.shift()!;
if (tempNode.left) helperQueue.push(tempNode.left);
if (tempNode.right) helperQueue.push(tempNode.right);
}
}
return resDepth;
};func maxDepth(_ root: TreeNode?) -> Int {
guard root != nil else { return 0 }
var depth = 0
var queue = [TreeNode]()
queue.append(root!)
while !queue.isEmpty {
let count = queue.count
depth += 1
for _ in 0 ..< count {
// 当前层
let node = queue.removeFirst()
// 下一层
if let node = node.left { queue.append(node) }
if let node = node.right { queue.append(node) }
}
}
return depth
}// 104.二叉树的最大深度
object Solution {
import scala.collection.mutable
def maxDepth(root: TreeNode): Int = {
if (root == null) return 0
val queue = mutable.Queue[TreeNode]()
queue.enqueue(root)
var depth = 0
while (!queue.isEmpty) {
val len = queue.length
depth += 1
for (i <- 0 until len) {
val curNode = queue.dequeue()
if (curNode.left != null) queue.enqueue(curNode.left)
if (curNode.right != null) queue.enqueue(curNode.right)
}
}
depth
}
}use std::cell::RefCell;
use std::collections::VecDeque;
use std::rc::Rc;
impl Solution {
pub fn max_depth(root: Option<Rc<RefCell<TreeNode>>>) -> i32 {
let mut queue = VecDeque::new();
let mut res = 0;
if root.is_some() {
queue.push_back(root);
}
while !queue.is_empty() {
res += 1;
for _ in 0..queue.len() {
let node = queue.pop_front().unwrap().unwrap();
if node.borrow().left.is_some() {
queue.push_back(node.borrow().left.clone());
}
if node.borrow().right.is_some() {
queue.push_back(node.borrow().right.clone());
}
}
}
res
}
}相对于 104.二叉树的最大深度 ,本题还也可以使用层序遍历的方式来解决,思路是一样的。
需要注意的是,只有当左右孩子都为空的时候,才说明遍历的最低点了。如果其中一个孩子为空则不是最低点
代码如下:(详细注释)
class Solution {
public:
int minDepth(TreeNode* root) {
if (root == NULL) return 0;
int depth = 0;
queue<TreeNode*> que;
que.push(root);
while(!que.empty()) {
int size = que.size();
depth++; // 记录最小深度
for (int i = 0; i < size; i++) {
TreeNode* node = que.front();
que.pop();
if (node->left) que.push(node->left);
if (node->right) que.push(node->right);
if (!node->left && !node->right) { // 当左右孩子都为空的时候,说明是最低点的一层了,退出
return depth;
}
}
}
return depth;
}
};class Solution {
public int minDepth(TreeNode root){
if (root == null) {
return 0;
}
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
int depth = 0;
while (!queue.isEmpty()){
int size = queue.size();
depth++;
TreeNode cur = null;
for (int i = 0; i < size; i++) {
cur = queue.poll();
//如果当前节点的左右孩子都为空,直接返回最小深度
if (cur.left == null && cur.right == null){
return depth;
}
if (cur.left != null) queue.offer(cur.left);
if (cur.right != null) queue.offer(cur.right);
}
}
return depth;
}
}# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def minDepth(self, root: TreeNode) -> int:
if not root:
return 0
depth = 0
queue = collections.deque([root])
while queue:
depth += 1
for _ in range(len(queue)):
node = queue.popleft()
if not node.left and not node.right:
return depth
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
return depth/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func minDepth(root *TreeNode) int {
ans := 0
if root == nil {
return 0
}
queue := list.New()
queue.PushBack(root)
for queue.Len() > 0 {
length := queue.Len()
for i := 0; i < length; i++ {
node := queue.Remove(queue.Front()).(*TreeNode)
if node.Left == nil && node.Right == nil { //当前节点没有左右节点,则代表此层是最小层
return ans+1 //返回当前层 ans代表是上一层
}
if node.Left != nil {
queue.PushBack(node.Left)
}
if node.Right != nil {
queue.PushBack(node.Right)
}
}
ans++//记录层数
}
return ans
}// 使用切片作为队列
func minDepth(root *TreeNode) int {
if root == nil {
return 0
}
depth := 0
queue := make([]*TreeNode, 0)
queue = append(queue, root)
for len(queue) > 0 {
size := len(queue)
depth++
for i := 0; i < size; i++ {
node := queue[0]
queue = queue[1:]
if node.Left != nil {
queue = append(queue, node.Left)
}
if node.Right != nil {
queue = append(queue, node.Right)
}
if node.Left == nil && node.Right == nil {
return depth
}
}
}
return depth
}/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number}
*/
var minDepth = function(root) {
if (root === null) return 0;
let queue = [root];
let depth = 0;
while (queue.length) {
let n = queue.length;
depth++;
for (let i=0; i<n; i++) {
let node = queue.shift();
// 如果左右节点都是null(在遇见的第一个leaf节点上),则该节点深度最小
if (node.left === null && node.right === null) {
return depth;
}
node.left && queue.push(node.left);;
node.right && queue.push(node.right);
}
}
return depth;
};function minDepth(root: TreeNode | null): number {
let helperQueue: TreeNode[] = [];
let resMin: number = 0;
let tempNode: TreeNode;
if (root !== null) helperQueue.push(root);
while (helperQueue.length > 0) {
resMin++;
for (let i = 0, length = helperQueue.length; i < length; i++) {
tempNode = helperQueue.shift()!;
if (tempNode.left === null && tempNode.right === null) return resMin;
if (tempNode.left !== null) helperQueue.push(tempNode.left);
if (tempNode.right !== null) helperQueue.push(tempNode.right);
}
}
return resMin;
};func minDepth(_ root: TreeNode?) -> Int {
guard root != nil else { return 0 }
var depth = 0
var queue = [root!]
while !queue.isEmpty {
let count = queue.count
depth += 1
for _ in 0 ..< count {
// 当前层
let node = queue.removeFirst()
if node.left == nil, node.right == nil { // 遇到叶子结点则返回
return depth
}
// 下一层
if let node = node.left { queue.append(node) }
if let node = node.right { queue.append(node) }
}
}
return depth
}// 111.二叉树的最小深度
object Solution {
import scala.collection.mutable
def minDepth(root: TreeNode): Int = {
if (root == null) return 0
var depth = 0
val queue = mutable.Queue[TreeNode]()
queue.enqueue(root)
while (!queue.isEmpty) {
depth += 1
val len = queue.size
for (i <- 0 until len) {
val curNode = queue.dequeue()
if (curNode.left != null) queue.enqueue(curNode.left)
if (curNode.right != null) queue.enqueue(curNode.right)
if (curNode.left == null && curNode.right == null) return depth
}
}
depth
}
}use std::cell::RefCell;
use std::collections::VecDeque;
use std::rc::Rc;
impl Solution {
pub fn min_depth(root: Option<Rc<RefCell<TreeNode>>>) -> i32 {
let mut res = 0;
let mut queue = VecDeque::new();
if root.is_some() {
queue.push_back(root);
}
while !queue.is_empty() {
res += 1;
for _ in 0..queue.len() {
let node = queue.pop_front().unwrap().unwrap();
if node.borrow().left.is_none() && node.borrow().right.is_none() {
return res;
}
if node.borrow().left.is_some() {
queue.push_back(node.borrow().left.clone());
}
if node.borrow().right.is_some() {
queue.push_back(node.borrow().right.clone());
}
}
}
res
}
}二叉树的层序遍历,就是图论中的广度优先搜索在二叉树中的应用,需要借助队列来实现(此时又发现队列的一个应用了)。
来吧,一口气打十个:
- 102.二叉树的层序遍历
- 107.二叉树的层次遍历II
- 199.二叉树的右视图
- 637.二叉树的层平均值
- 429.N叉树的层序遍历
- 515.在每个树行中找最大值
- 116.填充每个节点的下一个右侧节点指针
- 117.填充每个节点的下一个右侧节点指针II
- 104.二叉树的最大深度
- 111.二叉树的最小深度
致敬叶师傅!