参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！

101. 对称二叉树

力扣题目链接

给定一个二叉树，检查它是否是镜像对称的。

思路

《代码随想录》算法视频公开课：同时操作两个二叉树 | LeetCode：101. 对称二叉树，相信结合视频在看本篇题解，更有助于大家对本题的理解。

首先想清楚，判断对称二叉树要比较的是哪两个节点，要比较的可不是左右节点！

对于二叉树是否对称，要比较的是根节点的左子树与右子树是不是相互翻转的，理解这一点就知道了其实我们要比较的是两个树（这两个树是根节点的左右子树），所以在递归遍历的过程中，也是要同时遍历两棵树。

那么如何比较呢？

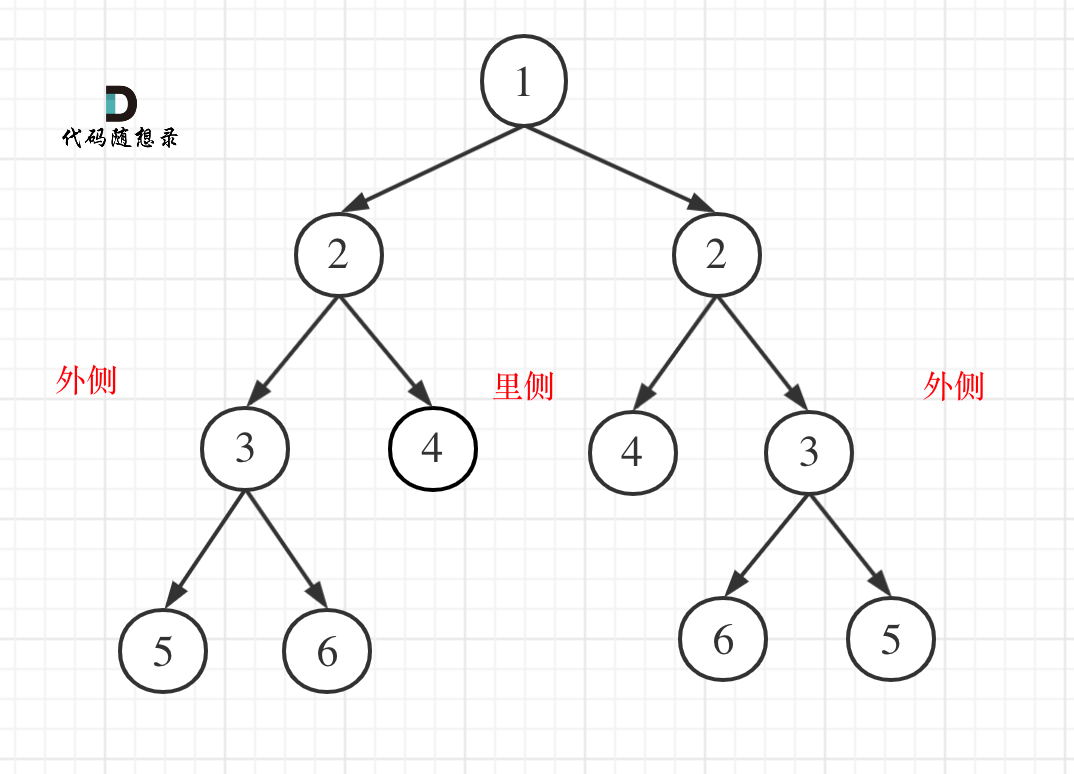
比较的是两个子树的里侧和外侧的元素是否相等。如图所示：

那么遍历的顺序应该是什么样的呢？

本题遍历只能是“后序遍历”，因为我们要通过递归函数的返回值来判断两个子树的内侧节点和外侧节点是否相等。

正是因为要遍历两棵树而且要比较内侧和外侧节点，所以准确的来说是一个树的遍历顺序是左右中，一个树的遍历顺序是右左中。

但都可以理解算是后序遍历，尽管已经不是严格上在一个树上进行遍历的后序遍历了。

其实后序也可以理解为是一种回溯，当然这是题外话，讲回溯的时候会重点讲的。

说到这大家可能感觉我有点啰嗦，哪有这么多道理，上来就干就完事了。别急，我说的这些在下面的代码讲解中都有身影。

那么我们先来看看递归法的代码应该怎么写。

递归法

递归三部曲

确定递归函数的参数和返回值

因为我们要比较的是根节点的两个子树是否是相互翻转的，进而判断这个树是不是对称树，所以要比较的是两个树，参数自然也是左子树节点和右子树节点。

返回值自然是bool类型。

代码如下：

bool compare(TreeNode* left, TreeNode* right)

确定终止条件

要比较两个节点数值相不相同，首先要把两个节点为空的情况弄清楚！否则后面比较数值的时候就会操作空指针了。

节点为空的情况有：（注意我们比较的其实不是左孩子和右孩子，所以如下我称之为左节点右节点）

左节点为空，右节点不为空，不对称，return false
左不为空，右为空，不对称 return false
左右都为空，对称，返回true

此时已经排除掉了节点为空的情况，那么剩下的就是左右节点不为空：

左右都不为空，比较节点数值，不相同就return false

此时左右节点不为空，且数值也不相同的情况我们也处理了。

代码如下：

if (left == NULL && right != NULL) return false;
else if (left != NULL && right == NULL) return false;
else if (left == NULL && right == NULL) return true;
else if (left->val != right->val) return false; // 注意这里我没有使用else

注意上面最后一种情况，我没有使用else，而是else if，因为我们把以上情况都排除之后，剩下的就是左右节点都不为空，且数值相同的情况。

确定单层递归的逻辑

此时才进入单层递归的逻辑，单层递归的逻辑就是处理左右节点都不为空，且数值相同的情况。

比较二叉树外侧是否对称：传入的是左节点的左孩子，右节点的右孩子。
比较内测是否对称，传入左节点的右孩子，右节点的左孩子。
如果左右都对称就返回true ，有一侧不对称就返回false 。

代码如下：

bool outside = compare(left->left, right->right);   // 左子树：左、 右子树：右
bool inside = compare(left->right, right->left);    // 左子树：右、 右子树：左
bool isSame = outside && inside;                    // 左子树：中、 右子树：中（逻辑处理）
return isSame;

如上代码中，我们可以看出使用的遍历方式，左子树左右中，右子树右左中，所以我把这个遍历顺序也称之为“后序遍历”（尽管不是严格的后序遍历）。

最后递归的C++整体代码如下：

class Solution {
public:
    bool compare(TreeNode* left, TreeNode* right) {
        // 首先排除空节点的情况
        if (left == NULL && right != NULL) return false;
        else if (left != NULL && right == NULL) return false;
        else if (left == NULL && right == NULL) return true;
        // 排除了空节点，再排除数值不相同的情况
        else if (left->val != right->val) return false;

        // 此时就是：左右节点都不为空，且数值相同的情况
        // 此时才做递归，做下一层的判断
        bool outside = compare(left->left, right->right);   // 左子树：左、 右子树：右
        bool inside = compare(left->right, right->left);    // 左子树：右、 右子树：左
        bool isSame = outside && inside;                    // 左子树：中、 右子树：中 （逻辑处理）
        return isSame;

    }
    bool isSymmetric(TreeNode* root) {
        if (root == NULL) return true;
        return compare(root->left, root->right);
    }
};

我给出的代码并不简洁，但是把每一步判断的逻辑都清楚的描绘出来了。

如果上来就看网上各种简洁的代码，看起来真的很简单，但是很多逻辑都掩盖掉了，而题解可能也没有把掩盖掉的逻辑说清楚。

盲目的照着抄，结果就是：发现这是一道“简单题”，稀里糊涂的就过了，但是真正的每一步判断逻辑未必想到清楚。

当然我可以把如上代码整理如下：

class Solution {
public:
    bool compare(TreeNode* left, TreeNode* right) {
        if (left == NULL && right != NULL) return false;
        else if (left != NULL && right == NULL) return false;
        else if (left == NULL && right == NULL) return true;
        else if (left->val != right->val) return false;
        else return compare(left->left, right->right) && compare(left->right, right->left);

    }
    bool isSymmetric(TreeNode* root) {
        if (root == NULL) return true;
        return compare(root->left, root->right);
    }
};

这个代码就很简洁了，但隐藏了很多逻辑，条理不清晰，而且递归三部曲，在这里完全体现不出来。

所以建议大家做题的时候，一定要想清楚逻辑，每一步做什么。把道题目所有情况想到位，相应的代码写出来之后，再去追求简洁代码的效果。

迭代法

这道题目我们也可以使用迭代法，但要注意，这里的迭代法可不是前中后序的迭代写法，因为本题的本质是判断两个树是否是相互翻转的，其实已经不是所谓二叉树遍历的前中后序的关系了。

这里我们可以使用队列来比较两个树（根节点的左右子树）是否相互翻转，（注意这不是层序遍历）

使用队列

通过队列来判断根节点的左子树和右子树的内侧和外侧是否相等，如动画所示：

如下的条件判断和递归的逻辑是一样的。

代码如下：

class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        if (root == NULL) return true;
        queue<TreeNode*> que;
        que.push(root->left);   // 将左子树头结点加入队列
        que.push(root->right);  // 将右子树头结点加入队列
        
        while (!que.empty()) {  // 接下来就要判断这两个树是否相互翻转
            TreeNode* leftNode = que.front(); que.pop();
            TreeNode* rightNode = que.front(); que.pop();
            if (!leftNode && !rightNode) {  // 左节点为空、右节点为空，此时说明是对称的
                continue;
            }

            // 左右一个节点不为空，或者都不为空但数值不相同，返回false
            if ((!leftNode || !rightNode || (leftNode->val != rightNode->val))) {
                return false;
            }
            que.push(leftNode->left);   // 加入左节点左孩子
            que.push(rightNode->right); // 加入右节点右孩子
            que.push(leftNode->right);  // 加入左节点右孩子
            que.push(rightNode->left);  // 加入右节点左孩子
        }
        return true;
    }
};

使用栈

细心的话，其实可以发现，这个迭代法，其实是把左右两个子树要比较的元素顺序放进一个容器，然后成对成对的取出来进行比较，那么其实使用栈也是可以的。

只要把队列原封不动的改成栈就可以了，我下面也给出了代码。

class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        if (root == NULL) return true;
        stack<TreeNode*> st; // 这里改成了栈
        st.push(root->left);
        st.push(root->right);
        while (!st.empty()) {
            TreeNode* leftNode = st.top(); st.pop();
            TreeNode* rightNode = st.top(); st.pop();
            if (!leftNode && !rightNode) {
                continue;
            }
            if ((!leftNode || !rightNode || (leftNode->val != rightNode->val))) {
                return false;
            }
            st.push(leftNode->left);
            st.push(rightNode->right);
            st.push(leftNode->right);
            st.push(rightNode->left);
        }
        return true;
    }
};

总结

这次我们又深度剖析了一道二叉树的“简单题”，大家会发现，真正的把题目搞清楚其实并不简单，leetcode上accept了和真正掌握了还是有距离的。

我们介绍了递归法和迭代法，递归依然通过递归三部曲来解决了这道题目，如果只看精简的代码根本看不出来递归三部曲是如何解题的。

在迭代法中我们使用了队列，需要注意的是这不是层序遍历，而且仅仅通过一个容器来成对的存放我们要比较的元素，知道这一本质之后就发现，用队列，用栈，甚至用数组，都是可以的。

如果已经做过这道题目的同学，读完文章可以再去看看这道题目，思考一下，会有不一样的发现！

其他语言版本

Java

    /**
     * 递归法
     */
    public boolean isSymmetric1(TreeNode root) {
        return compare(root.left, root.right);
    }

    private boolean compare(TreeNode left, TreeNode right) {

        if (left == null && right != null) {
            return false;
        }
        if (left != null && right == null) {
            return false;
        }

        if (left == null && right == null) {
            return true;
        }
        if (left.val != right.val) {
            return false;
        }
        // 比较外侧
        boolean compareOutside = compare(left.left, right.right);
        // 比较内侧
        boolean compareInside = compare(left.right, right.left);
        return compareOutside && compareInside;
    }

    /**
     * 迭代法
     * 使用双端队列，相当于两个栈
     */
    public boolean isSymmetric2(TreeNode root) {
        Deque<TreeNode> deque = new LinkedList<>();
        deque.offerFirst(root.left);
        deque.offerLast(root.right);
        while (!deque.isEmpty()) {
            TreeNode leftNode = deque.pollFirst();
            TreeNode rightNode = deque.pollLast();
            if (leftNode == null && rightNode == null) {
                continue;
            }
//            if (leftNode == null && rightNode != null) {
//                return false;
//            }
//            if (leftNode != null && rightNode == null) {
//                return false;
//            }
//            if (leftNode.val != rightNode.val) {
//                return false;
//            }
            // 以上三个判断条件合并
            if (leftNode == null || rightNode == null || leftNode.val != rightNode.val) {
                return false;
            }
            deque.offerFirst(leftNode.left);
            deque.offerFirst(leftNode.right);
            deque.offerLast(rightNode.right);
            deque.offerLast(rightNode.left);
        }
        return true;
    }

    /**
     * 迭代法
     * 使用普通队列
     */
    public boolean isSymmetric3(TreeNode root) {
        Queue<TreeNode> deque = new LinkedList<>();
        deque.offer(root.left);
        deque.offer(root.right);
        while (!deque.isEmpty()) {
            TreeNode leftNode = deque.poll();
            TreeNode rightNode = deque.poll();
            if (leftNode == null && rightNode == null) {
                continue;
            }
//            if (leftNode == null && rightNode != null) {
//                return false;
//            }
//            if (leftNode != null && rightNode == null) {
//                return false;
//            }
//            if (leftNode.val != rightNode.val) {
//                return false;
//            }
            // 以上三个判断条件合并
            if (leftNode == null || rightNode == null || leftNode.val != rightNode.val) {
                return false;
            }
            // 这里顺序与使用Deque不同
            deque.offer(leftNode.left);
            deque.offer(rightNode.right);
            deque.offer(leftNode.right);
            deque.offer(rightNode.left);
        }
        return true;
    }

Python

递归法:

class Solution:
    def isSymmetric(self, root: TreeNode) -> bool:
        if not root:
            return True
        return self.compare(root.left, root.right)
        
    def compare(self, left, right):
        #首先排除空节点的情况
        if left == None and right != None: return False
        elif left != None and right == None: return False
        elif left == None and right == None: return True
        #排除了空节点，再排除数值不相同的情况
        elif left.val != right.val: return False
        
        #此时就是：左右节点都不为空，且数值相同的情况
        #此时才做递归，做下一层的判断
        outside = self.compare(left.left, right.right) #左子树：左、 右子树：右
        inside = self.compare(left.right, right.left) #左子树：右、 右子树：左
        isSame = outside and inside #左子树：中、 右子树：中 （逻辑处理）
        return isSame

迭代法：使用队列

import collections
class Solution:
    def isSymmetric(self, root: TreeNode) -> bool:
        if not root:
            return True
        queue = collections.deque()
        queue.append(root.left) #将左子树头结点加入队列
        queue.append(root.right) #将右子树头结点加入队列
        while queue: #接下来就要判断这这两个树是否相互翻转
            leftNode = queue.popleft()
            rightNode = queue.popleft()
            if not leftNode and not rightNode: #左节点为空、右节点为空，此时说明是对称的
                continue
            
            #左右一个节点不为空，或者都不为空但数值不相同，返回false
            if not leftNode or not rightNode or leftNode.val != rightNode.val:
                return False
            queue.append(leftNode.left) #加入左节点左孩子
            queue.append(rightNode.right) #加入右节点右孩子
            queue.append(leftNode.right) #加入左节点右孩子
            queue.append(rightNode.left) #加入右节点左孩子
        return True

迭代法：使用栈

class Solution:
    def isSymmetric(self, root: TreeNode) -> bool:
        if not root:
            return True
        st = [] #这里改成了栈
        st.append(root.left)
        st.append(root.right)
        while st:
            rightNode = st.pop()
            leftNode = st.pop()
            if not leftNode and not rightNode:
                continue
            if not leftNode or not rightNode or leftNode.val != rightNode.val:
                return False
            st.append(leftNode.left)
            st.append(rightNode.right)
            st.append(leftNode.right)
            st.append(rightNode.left)
        return True

层次遍历

class Solution:
    def isSymmetric(self, root: Optional[TreeNode]) -> bool:
        if not root:
            return True

        que = [root]
        while que:
            this_level_length = len(que)
            for i in range(this_level_length // 2):
                # 要么其中一个是None但另外一个不是
                if (not que[i] and que[this_level_length - 1 - i]) or (que[i] and not que[this_level_length - 1 - i]):
                    return False
                # 要么两个都不是None
                if que[i] and que[i].val != que[this_level_length - 1 - i].val:
                    return False
            for i in range(this_level_length):
                if not que[i]: continue
                que.append(que[i].left)
                que.append(que[i].right)
            que = que[this_level_length:]
        return True

Go

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
// 递归
func defs(left *TreeNode, right *TreeNode) bool {
    if left == nil && right == nil {
        return true;
    };
    if left == nil || right == nil {
        return false;
    };
    if left.Val != right.Val {
        return false;
    }
    return defs(left.Left, right.Right) && defs(right.Left, left.Right);
}

func isSymmetric(root *TreeNode) bool {
    return defs(root.Left, root.Right);
}


// 迭代
func isSymmetric(root *TreeNode) bool {
    var queue []*TreeNode;
    if root != nil {
        queue = append(queue, root.Left, root.Right);
    }
    for len(queue) > 0 {
        left := queue[0];
        right := queue[1];
        queue = queue[2:];
        if left == nil && right == nil {
            continue;
        }
        if left == nil || right == nil || left.Val != right.Val {
            return false;
        };
        queue = append(queue, left.Left, right.Right, right.Left, left.Right);
    }
    return true;
}

JavaScript

递归判断是否为对称二叉树：

var isSymmetric = function(root) {
    // 使用递归遍历左右子树 递归三部曲
    // 1. 确定递归的参数 root.left root.right和返回值true false 
    const compareNode = function(left, right) {
        // 2. 确定终止条件 空的情况
        if(left === null && right !== null || left !== null && right === null) {
            return false;
        } else if(left === null && right === null) {
            return true;
        } else if(left.val !== right.val) {
            return false;
        }
        // 3. 确定单层递归逻辑
        let outSide = compareNode(left.left, right.right);
        let inSide = compareNode(left.right, right.left);
        return outSide && inSide;
    }
    if(root === null) {
        return true;
    }
    return compareNode(root.left, root.right);
};

队列实现迭代判断是否为对称二叉树：

var isSymmetric = function(root) {
  // 迭代方法判断是否是对称二叉树
  // 首先判断root是否为空
  if(root === null) {
      return true;
  }
  let queue = [];
  queue.push(root.left);
  queue.push(root.right);
  while(queue.length) {
      let leftNode = queue.shift();    //左节点
      let rightNode = queue.shift();   //右节点
      if(leftNode === null && rightNode === null) {
          continue;
      }
      if(leftNode === null || rightNode === null || leftNode.val !== rightNode.val) {
          return false;
      }
      queue.push(leftNode.left);     //左节点左孩子入队
      queue.push(rightNode.right);   //右节点右孩子入队
      queue.push(leftNode.right);    //左节点右孩子入队
      queue.push(rightNode.left);    //右节点左孩子入队
  }
  
  return true;
};

栈实现迭代判断是否为对称二叉树：

var isSymmetric = function(root) {
  // 迭代方法判断是否是对称二叉树
  // 首先判断root是否为空
  if(root === null) {
      return true;
  }
  let stack = [];
  stack.push(root.left);
  stack.push(root.right);
  while(stack.length) {
      let rightNode = stack.pop();    //左节点
      let leftNode=stack.pop();       //右节点
      if(leftNode === null && rightNode === null) {
          continue;
      }
      if(leftNode === null || rightNode === null || leftNode.val !== rightNode.val) {
          return false;
      }
      stack.push(leftNode.left);      //左节点左孩子入队
      stack.push(rightNode.right);    //右节点右孩子入队
      stack.push(leftNode.right);     //左节点右孩子入队
      stack.push(rightNode.left);     //右节点左孩子入队
  }
  
  return true;
};

TypeScript：

递归法

function isSymmetric(root: TreeNode | null): boolean {
    function recur(node1: TreeNode | null, node2: TreeNode | null): boolean {
        if (node1 === null && node2 === null) return true;
        if (node1 === null || node2 === null) return false;
        if (node1.val !== node2.val) return false
        let isSym1: boolean = recur(node1.left, node2.right);
        let isSym2: boolean = recur(node1.right, node2.left);
        return isSym1 && isSym2
    }
    if (root === null) return true;
    return recur(root.left, root.right);
};

迭代法

// 迭代法(队列)
function isSymmetric(root: TreeNode | null): boolean {
    let helperQueue: (TreeNode | null)[] = [];
    let tempNode1: TreeNode | null,
        tempNode2: TreeNode | null;
    if (root !== null) {
        helperQueue.push(root.left);
        helperQueue.push(root.right);
    }
    while (helperQueue.length > 0) {
        tempNode1 = helperQueue.shift()!;
        tempNode2 = helperQueue.shift()!;
        if (tempNode1 === null && tempNode2 === null) continue;
        if (tempNode1 === null || tempNode2 === null) return false;
        if (tempNode1.val !== tempNode2.val) return false;
        helperQueue.push(tempNode1.left);
        helperQueue.push(tempNode2.right);
        helperQueue.push(tempNode1.right);
        helperQueue.push(tempNode2.left);
    }
    return true;
}

// 迭代法(栈)
function isSymmetric(root: TreeNode | null): boolean {
    let helperStack: (TreeNode | null)[] = [];
    let tempNode1: TreeNode | null,
        tempNode2: TreeNode | null;
    if (root !== null) {
        helperStack.push(root.left);
        helperStack.push(root.right);
    }
    while (helperStack.length > 0) {
        tempNode1 = helperStack.pop()!;
        tempNode2 = helperStack.pop()!;
        if (tempNode1 === null && tempNode2 === null) continue;
        if (tempNode1 === null || tempNode2 === null) return false;
        if (tempNode1.val !== tempNode2.val) return false;
        helperStack.push(tempNode1.left);
        helperStack.push(tempNode2.right);
        helperStack.push(tempNode1.right);
        helperStack.push(tempNode2.left);
    }
    return true;
};

Swift:

递归

func isSymmetric(_ root: TreeNode?) -> Bool {
    return _isSymmetric(root?.left, right: root?.right)
}
func _isSymmetric(_ left: TreeNode?, right: TreeNode?) -> Bool {
    // 首先排除空节点情况
    if left == nil && right == nil {
        return true
    } else if left == nil && right != nil {
        return false
    } else if left != nil && right == nil {
        return false
    } else if left!.val != right!.val {
        // 进而排除数值不相等的情况
        return false
    }
    
    // left 和 right 都不为空, 且数值也相等就递归
    let inSide = _isSymmetric(left!.right, right: right!.left)
    let outSide = _isSymmetric(left!.left, right: right!.right)
    return inSide && outSide
}

迭代 - 使用队列

func isSymmetric2(_ root: TreeNode?) -> Bool {
    guard let root = root else {
        return true
    }
    var queue = [TreeNode?]()
    queue.append(root.left)
    queue.append(root.right)
    while !queue.isEmpty {
        let left = queue.removeFirst()
        let right = queue.removeFirst()
        if left == nil && right == nil {
            continue
        }
        if left == nil || right == nil || left?.val != right?.val {
            return false
        }
        queue.append(left!.left)
        queue.append(right!.right)
        queue.append(left!.right)
        queue.append(right!.left)
    }
    return true
}

迭代 - 使用栈

func isSymmetric3(_ root: TreeNode?) -> Bool {
    guard let root = root else {
        return true
    }
    var stack = [TreeNode?]()
    stack.append(root.left)
    stack.append(root.right)
    while !stack.isEmpty {
        let left = stack.removeLast()
        let right = stack.removeLast()
        
        if left == nil && right == nil {
            continue
        }
        if left == nil || right == nil || left?.val != right?.val {
            return false
        }
        stack.append(left!.left)
        stack.append(right!.right)
        stack.append(left!.right)
        stack.append(right!.left)
    }
    return true
}

Scala

递归：

object Solution { 
  def isSymmetric(root: TreeNode): Boolean = {
    if (root == null) return true // 如果等于空直接返回true
    
    def compare(left: TreeNode, right: TreeNode): Boolean = {
      if (left == null && right == null) true // 如果左右都为空，则为true
      else if (left == null && right != null) false // 如果左空右不空，不对称，返回false
      else if (left != null && right == null) false // 如果左不空右空，不对称，返回false
      // 如果左右的值相等，并且往下递归
      else left.value == right.value && compare(left.left, right.right) && compare(left.right, right.left)
    }
    
    // 分别比较左子树和右子树
    compare(root.left, root.right)
  }
}

迭代 - 使用栈

object Solution {

  import scala.collection.mutable

  def isSymmetric(root: TreeNode): Boolean = {
    if (root == null) return true

    val cache = mutable.Stack[(TreeNode, TreeNode)]((root.left, root.right))
    
    while (cache.nonEmpty) {
      cache.pop() match {
        case (null, null) =>
        case (_, null) => return false
        case (null, _) => return false
        case (left, right) =>
          if (left.value != right.value) return false
          cache.push((left.left, right.right))
          cache.push((left.right, right.left))
      }
    }
    true
  }
}

迭代 - 使用队列

object Solution {

  import scala.collection.mutable

  def isSymmetric(root: TreeNode): Boolean = {
    if (root == null) return true

    val cache = mutable.Queue[(TreeNode, TreeNode)]((root.left, root.right))
    
    while (cache.nonEmpty) {
      cache.dequeue() match {
        case (null, null) =>
        case (_, null) => return false
        case (null, _) => return false
        case (left, right) =>
          if (left.value != right.value) return false
          cache.enqueue((left.left, right.right))
          cache.enqueue((left.right, right.left))
      }
    }
    true
  }
}

Rust

递归：

impl Solution {
    pub fn is_symmetric(root: Option<Rc<RefCell<TreeNode>>>) -> bool {
        Self::recur(
            &root.as_ref().unwrap().borrow().left,
            &root.as_ref().unwrap().borrow().right,
        )
    }
    pub fn recur(
        left: &Option<Rc<RefCell<TreeNode>>>,
        right: &Option<Rc<RefCell<TreeNode>>>,
    ) -> bool {
        match (left, right) {
            (None, None) => true,
            (Some(n1), Some(n2)) => {
                return n1.borrow().val == n2.borrow().val
                    && Self::recur(&n1.borrow().left, &n2.borrow().right)
                    && Self::recur(&n1.borrow().right, &n2.borrow().left)
            }
            _ => false,
        }
    }
}

迭代：

use std::cell::RefCell;
use std::collections::VecDeque;
use std::rc::Rc;
impl Solution {
    pub fn is_symmetric(root: Option<Rc<RefCell<TreeNode>>>) -> bool {
        let mut queue = VecDeque::new();
        if let Some(node) = root {
            queue.push_back(node.borrow().left.clone());
            queue.push_back(node.borrow().right.clone());
        }
        while !queue.is_empty() {
            let (n1, n2) = (queue.pop_front().unwrap(), queue.pop_front().unwrap());
            match (n1.clone(), n2.clone()) {
                (None, None) => continue,
                (Some(n1), Some(n2)) => {
                    if n1.borrow().val != n2.borrow().val {
                        return false;
                    }
                }
                _ => return false,
            };
            queue.push_back(n1.as_ref().unwrap().borrow().left.clone());
            queue.push_back(n2.as_ref().unwrap().borrow().right.clone());
            queue.push_back(n1.unwrap().borrow().right.clone());
            queue.push_back(n2.unwrap().borrow().left.clone());
        }
        true
    }
}

Provide feedback

Saved searches

Use saved searches to filter your results more quickly

0101.对称二叉树.md

0101.对称二叉树.md

101. 对称二叉树

思路

递归法

迭代法

使用队列

使用栈

总结

相关题目推荐

其他语言版本

Rust

Files

0101.对称二叉树.md

Latest commit

History

0101.对称二叉树.md

File metadata and controls

101. 对称二叉树

思路

递归法

迭代法

使用队列

使用栈

总结

相关题目推荐

其他语言版本

Rust