本文将通过绘制一个心形示例,来回顾和复习一下前面学习的 顶点缓冲区 和 缓冲区资源绑定。
本示例的大体步骤:
- 通过一个特定的公式和一些系数,得到一组心形的顶点坐标
- 将这些坐标写入到顶点缓冲区中,供顶点着色器使用
- 配置渲染管线,把这些顶点依次连接起来,形成一些线稿形式的图像
- 同时,通过 JS 可以修改得到一个 RGB 颜色值,并将其作为 缓冲区 进行资源绑定,供片元着色器读取这个颜色值
- 修改公式中的不同系数值,可以得到除了 心形 以外的其他图形
- 本示例使用了
react-dat-gui这个 NPM 包来作为调整各项系数的控件
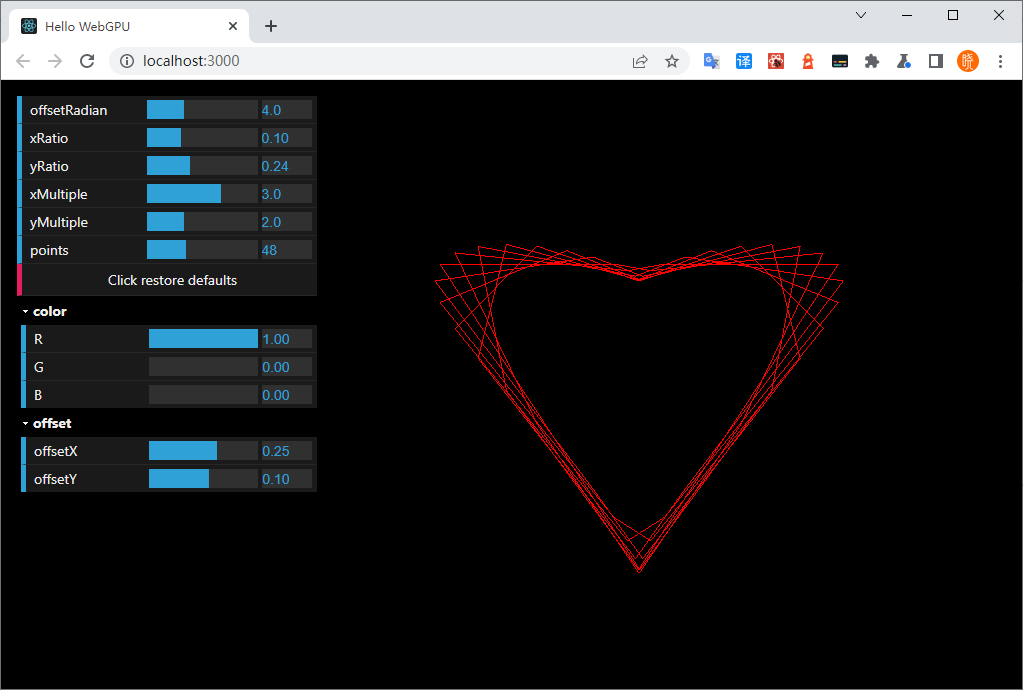
先看最终绘制的结果:
本示例的临时在线演示地址:https://react-webgpu-samples.vercel.app/
为什么说是临时地址呢?因为以后要再做其他示例,或许就会覆盖掉它。
特别说明:在页面头部信息中,我已配置了 源测试令牌(origin trial),所以你可以直接使用 谷歌浏览器打开,默认就会自动唤醒 WebGPU ,无需使用 金丝雀版本开启 WebGPU。
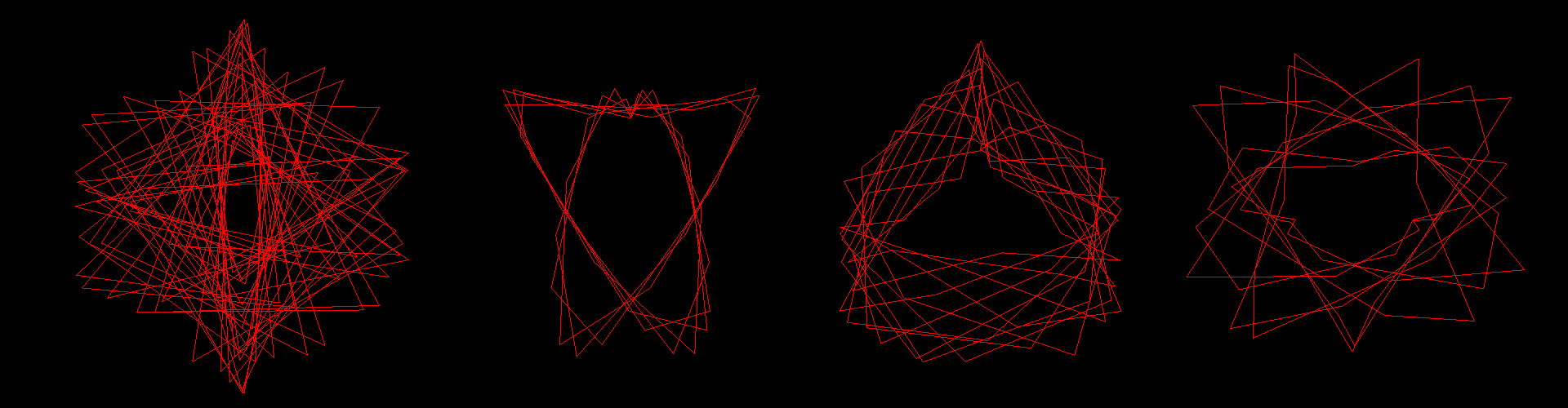
为什么标题上要加上 “奇怪” 二字呢?
因为生成这个心形的坐标公式中,稍微修改其中几个系数大小,那么得到的就不是心形,而是下面一些很奇怪的图形。
介绍一下 心形 坐标公式
心形的坐标公式有很多,因为心形弧度不同其坐标公式也不同。
在本示例中,我们依然假定每个顶点坐标的 z 坐标永远为 0,我们需要计算的是 x, y 坐标,因此你可以把它当成一个 二维的直角坐标系 来看。
在本示例中,我们基于以下这个心形坐标公式:
x = a(3*sin(θ) - sin(3θ))
y = 2a(2*cos(θ) - cos(2θ))
心形坐标函数最著名的莫过于 笛卡尔 爱情故事中的 r=a(1-sinθ),在这个公式中 r 表示极坐标中 点与圆形的距离,θ 为点与 x 轴的夹角,a 为一个系数。
电视剧《隐秘的角落》中提及过这个公式。
直角坐标系,创始人是 笛卡尔,直角坐标系也被称为 笛卡尔坐标系。
极坐标 的创始人是牛顿。
直角坐标系中是通过 x, y 坐标值来定位一个 点 的位置。
极坐标则是通过 r, θ 来定位一个点的位置
上面提到的 极坐标 默认是指 二维的,在 3D 球形中使用的是 3 维极坐标,通常称呼为 “球极坐标”。
和本文无关的废话有点多...
回到本文正题。
特别提醒:对于 示例 而言,直接看代码比看下面写的讲解步骤,效率反而会更高一些。
本示例的代码地址:
https://github.com/puxiao/react-webgpu-samples/blob/main/src/components/heart-shape/index.tsx
本示例中用户可调节的系数
本示例使用了 TypeScript,所以先定义那些用户可以控制调节的各项系数。
interface GuiData {
offsetRadian: number
xRatio: number
yRatio: number
xMultiple: number
yMultiple: number
points: number
r: number
g: number
b: number
offsetX: number
offsetY: number
}
// 各项系数默认值,这些值可以绘制出一个比较正的心形图案
let guiDataInit: GuiData = {
offsetRadian: 4,
xRatio: 0.1,
yRatio: 0.24,
xMultiple: 3,
yMultiple: 2,
points: 48,
r: 1,
g: 0,
b: 0,
offsetX: 0,
offsetY: 0.1
}
- offsetRadian:用来控制每一次绘制点时的角度偏移量
- xRatio、yRatio:x,y 中 a 的系数值
- xMultiple、yMultiple:x,y 括号中的系数值
- points:设定顶点的总数,我们假定它一定是大于或等于 4 ,且一定是 2 的整倍数
- r,g,b:一个 RGB 颜色值的 3 个分量
- offsetX、offsetY:x,y 整体的偏移量
生成顶点坐标的 JS 函数:
const getHeartXYArr = (data: GuiData) => {
const { offsetRadian, xRatio, yRatio, xMultiple, yMultiple, points, offsetX, offsetY } = data
const radian = Math.PI * 2 / points
const res: number[] = []
let rad: number = 0
for (let i = 0; i < points; i++) {
rad = (radian + Math.PI / offsetRadian) * i
res.push(xRatio * (xMultiple * Math.sin(rad) - Math.sin(xMultiple * rad)) + offsetX)
res.push(yRatio * (yMultiple * Math.cos(rad) - Math.cos(yMultiple * rad)) + offsetY)
}
res.push(res[0], res[1])
return res
}
请注意上述代码中,我们在获得了各个关键的顶点坐标信息后,在数组的结尾处重新添加了一次第一个顶点坐标,这样做的目的是为了让线段绘制可以 “首尾相连”,即 最后一个坐标点连接到最开始的坐标点上。
配置管线中关于顶点的拓扑关系
在之前绘制一个三角形的示例中,此处的配置为:
primitive: {
topology: 'triangle-strip'
}
'triangle-strip' 表示:三个点组成一个实心的三角形
而在本示例中,我们此处的配置修改为:
primitive: {
topology: 'line-strip'
}
'line-strip' 表示:点与点之间依次连接,形成线段
关于 react-dat-gui 的介绍
我平时主要使用 React,GUI 控件有很多,而我一直习惯使用 react-dat-gui。
yarn add react-dat-gui
Three.js 官方示例中很多使用的是 mrdoob 编写的
dat.gui当然也有使用
lil-gui这个的。
关于本示例中的一些关键点信息,我已经讲完了(实际这些信息和 WebGPU 关联并不大),其他相关的代码和我们之前示例中的相差不多。
我更推荐你直接去看本示例源码,再次说一遍,本示例的代码地址:
https://github.com/puxiao/react-webgpu-samples/blob/main/src/components/heart-shape/index.tsx
关于一些代码组织的反思
本示例实际上是我编写的第一个具有交互性质的 WebGPU 示例,尽管并不复杂,但是随着代码量的变多,代码的可阅读性、复用性 在降低。
因为我把大量的代码写在了 useEffect() 中,这点肯定是不好的,我会慢慢改进的。
留给读者的思考题
本示例中绘制的是心形线条,假设要绘制实心的心形,又该怎么实现呢?
在目前的所有示例中,我们实际上都是把整个 WebGPU 画布当做了一个 二维的画布来使用,因为我们所有的顶点坐标 z 轴都设置的是 0。
下一节,我们将系统的学习一下 WebGPU 中的 3D 空间相关概念,揭开 z 轴的奥秘。
本文到此结束。