As the name suggests, a monotonic stack is a kind of stack. Therefore, to learn monotonic stacks, you must first thoroughly understand the stacks.
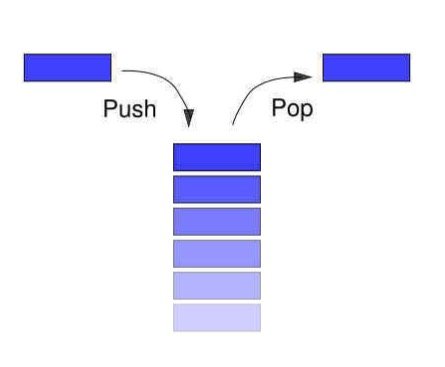
The stack is a restricted data structure, which is reflected in the fact that only new content is allowed to be inserted or deleted from one direction. This direction is called the top of the stack, and obtaining content from other locations is not allowed.
The most distinctive feature of the stack is LIFO (Last In, First Out-last In, First Out)
Give an example:
The stack is like a drawer for books. The operation of entering the stack is like trying to put a book in the drawer. The newly entered book is always at the top, while exiting the stack is equivalent to taking the book from the inside out, always starting from the top, so the one that is taken out is always the last one to go in.
- Stack-push-place elements to the top of the stack
- Backstack-pop-pop up the top element of the stack
- Stack top-top-get the value of the top element of the stack
- Whether the stack is empty-isEmpty-determines whether there are elements in the stack
Since the stack only operates at the end, if we use arrays for simulation, the time complexity of O(1) can be easily achieved. Of course, it can also be implemented with a linked list, that is, a chain stack.
- In-stack-O (1)
- Out of the stack-O (1)
-Function call stack -Browser forward and backward -Matching brackets -The monotonic stack is used to find the next larger (smaller) element
- [394. String decoding](https://leetcode-cn.com/problems/decode-string /)
- [946. Verify stack sequence](https://leetcode-cn.com/problems/validate-stack-sequences /)
- [1381. Design a stack that supports incremental operations](https://leetcode-cn.com/problems/design-a-stack-with-increment-operation /)
A monotonic stack is a special kind of stack. The stack is originally a restricted data structure, and the monotonic stack is restricted again (restricted ++) on this basis.
A monotonic stack requires that the elements in the stack are monotonically decreasing or monotonically decreasing.
Whether it is strictly decreasing or decreasing can be determined according to the actual situation.
Here I use [a, b, c] to represent a stack. Among them, the left side is the bottom of the stack and the right side is the top of the stack. Monotonically increasing or monotonically decreasing depends on the order in which the stack is released. If the elements out of the stack are monotonically increasing, it is monotonically increasing the stack, and if the elements out of the stack are monotonically decreasing, it is monotonically decreasing the stack.
For example:
-[1,2,3,4] is a monotonically decreasing stack (because the order of stacks at this time is 4,3,2,1. The same below, not repeat them) -[3,2,1] is a monotonically increasing stack -[1,3,2] is not a legal monotonic stack
So what is the use of this restriction? What kind of problem can this restriction (feature) solve?
The suitable topic for monotonic stack is to solve the following questions: The next one is greater than xxx or The next one is less than xxx. All when you have this kind of demand, you should think of monotonic stacks.
So why is the monotonic stack suitable for solving the problem of The next one is greater than xxx or the next one is less than xxx? The reason is very simple, let me explain it to you with an example.
The example given here is a monotonically decreasing stack
For example, we need to press the array [1,3,4,5,2,9,6] into the monotonic stack in turn.
- First press 1, the stack at this time is:[1]
- Continue to press into 3, the stack at this time is: [1,3]
- Continue to press into 4, the stack at this time is: [1,3,4]
- Continue to press into 5, the stack at this time is: [1,3,4,5]
- **If **continues to press into 2, the stack at this time is: [1,3,4,5,2] does not meet the characteristics of monotonically decreasing the stack, so it needs to be adjusted. How to adjust? Since the stack only has pop operations, we have to keep pop until the monotonous decrement is satisfied.
- In fact, we did not press into 2 above, but first pop. Until pop is pressed into 2, we can still keep monotonically decreasing and then press into 2. At this time, the stack is: [1,2]
- Continue to press into 9, the stack at this time is: [1,2,9]
- **If **Continues to press into 6, the characteristics of the monotonically decreasing stack are not satisfied. We repeat the technique and continue to pop until the monotonically decreasing stack is satisfied. The stack at this time is: [1,2,6]
Note that the stack here is still non-empty. If some topics need to use all the array information, then it is very likely that all test cases cannot be passed because the boundaries are not considered. Here is a technique -Sentinel Method, which is often used in monotonic stack algorithms.
For the above example, I can add an item smaller than the minimum value in the array to the right side of the original array [1,3,4,5,2,9,6], such as -1. The array at this time is [1,3,4,5,2,9,6, -1]. This technique can simplify the code logic, and everyone can master it as much as possible.
If you understand the above example, it is not difficult to understand why the monotonic stack is suitable for solving problems such as ** The next one is greater than xxx** or ** the next one is less than xxx**. For example, in the above example, we can easily find the position of the first one after it is smaller than itself. For example, the index of 3 is 1, the first index less than 3 is 4, the index of 2 is 4, and the first index less than 2 is 0, but it is after the index of 2 is 4, so it does not meet the condition, that is, there is no position after 2 that is less than 2 itself.
In the above example, we started pop in step 6, and the first one that was pop out was 5, so the first index less than 5 after 5 is 4. Similarly, the 3, 4, and 5 that are pop out are all 4.
If ans is used to denote the first position after arr[i] that is less than itself, ans[i] represents the first position after arr[i] that is less than arr[i], and ans[i] is -1 to indicate that such a position does not exist, such as the 2 mentioned earlier. Then the ans at this time is [-1,4,4,4,-1,-1,-1]。
Step 8, we are starting to pop again. At this time, 9 pops up, so the first index less than 9 after 9 is 6.
The process of this algorithm is summed up in one sentence, **If the monotonicity can still be maintained after pressing the stack, then directly press. Otherwise, the elements of the stack will pop up first, and the monotonicity will be maintained until they are pressed in. ** The principle of this algorithm is summed up in one sentence, The elements that are popped up are all larger than the current element, and since the stack is monotonically increasing, the nearest one that is smaller than itself after it is the current element.
Let's recommend a few questions for everyone. While the knowledge is still in your mind, hurry up and brush it up~
The above algorithm can be represented by the following pseudo-code. At the same time, this is a general algorithm template. You can directly solve the problem of monotonic stack.
It is recommended that everyone implement it in a programming language that they are familiar with, and you can basically use it by changing the symbols in the future.
class Solution:
def monostoneStack(self, arr: List[int]) -> List[int]:
stack = []
ans = Define an array of the same length as arr and initialize it to -1
Cycle i in arr:
While stack and arr[i]>arr[element at the top of the stack]:
peek = Pop up the top element of the stack
ans[peek] = i - peek
stack. append(i)
return ansComplexity analysis
-Time complexity: Since the elements of arr will only enter the stack and exit the stack once at most, the time complexity is still
Here are the monotonic stack templates for the two programming languages for your reference.
Python3:
class Solution:
def monostoneStack(self, T: List[int]) -> List[int]:
stack = []
ans = [0] * len(T)
for i in range(len(T)):
while stack and T[i] > T[stack[-1]]:
peek = stack. pop(-1)
ans[peek] = i - peek
stack. append(i)
return ansJS:
var monostoneStack = function (T) {
let stack = [];
let result = [];
for (let i = 0; i < T.length; i++) {
result[i] = 0;
while (stack.length > 0 && T[stack[stack.length - 1]] < T[i]) {
let peek = stack.pop();
result[peek] = i - peek;
}
stack.push(i);
}
return result;
};The following questions will help you understand the monotonic stack and let you understand when you can use the monotonic stack for algorithm optimization.
-
- Remove duplicate letters
-
- Remove K digits
-
- The next larger element I
-
- Shortest unordered continuous subarray
-
- Stock price span
The monotonic stack is essentially a stack, and the stack itself is a restricted data structure. Its restriction refers to the fact that it can only operate at one end. The monotonic stack is further restricted on the basis of the stack, that is, the elements in the stack are required to maintain monotonicity at all times.
Since the stack is monotonous, it is naturally suitable for solving the problem that the first position after it is smaller than its own position. If you encounter a topic and need to find the first topic after it that is smaller than its own position, you can consider using the monotonic stack.
The writing method of monotonic stack is relatively fixed. You can refer to my pseudo-code to summarize a template by yourself. Applying it directly in the future can greatly improve the efficiency and fault tolerance of problem-solving.