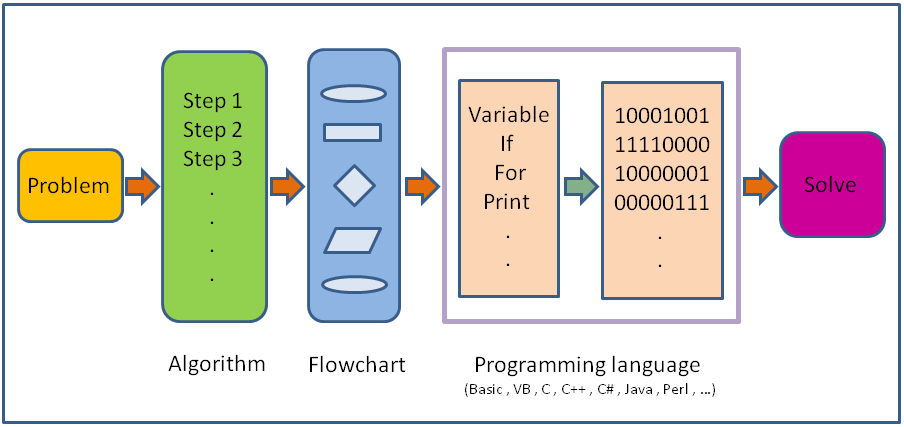
La risoluzione di un problema è un processo sistematico che parte da una situazione iniziale (il problema) e arriva a una situazione finale (la soluzione), seguendo un metodo o una serie di passaggi predefiniti.
-
Definizione del problema
Si parte dall’identificazione chiara e completa del problema, specificando i dati iniziali e i risultati desiderati. -
Individuazione del metodo risolutivo
Si determina un approccio o una strategia per passare dai dati iniziali ai risultati finali. Questo approccio può includere formule, algoritmi o sequenze di azioni logiche. -
Esecuzione del processo risolutivo
Si applica il metodo scelto, trasformando i dati di input in output.
-
Insieme ordinato di azioni elementari
Il processo viene suddiviso in una sequenza di passaggi semplici, ognuno dei quali esegue una piccola parte del lavoro. Questo rende il processo più facile da comprendere, ripetere e automatizzare. -
Eseguibilità da un elaboratore
Se ogni passaggio del processo è:- Comprensibile da un computer (espresso in istruzioni che il computer può interpretare, ad esempio tramite un linguaggio di programmazione),
- Eseguibile (non richiede interventi esterni o passaggi ambigui),
allora l’intero processo può essere automatizzato ed eseguito da un elaboratore.
Problema: Calcolare la somma di tutti i numeri pari in un elenco.
Dati iniziali: Un elenco di numeri (ad esempio, [1, 2, 3, 4, 5]).
Risultato atteso: La somma dei numeri pari (2 + 4 = 6).
- Inizializzare una variabile somma a 0.
- Per ogni numero nell’elenco:
- Controllare se è pari.
- Se è pari, aggiungerlo alla somma.
- Restituire il valore della somma.
Se questo metodo è tradotto in un linguaggio comprensibile per un elaboratore (ad esempio, Python):
numeri = [1, 2, 3, 4, 5]
somma = 0
for numero in numeri:
if numero % 2 == 0: # Controlla se è pari
somma += numero
print(somma) # Output: 6Questo esempio dimostra come un processo risolutivo strutturato possa essere eseguito manualmente o automatizzato da un computer.
Non tutti i problemi possono essere affrontati e risolti da un elaboratore. Questo può dipendere dalla natura del problema, dalla mancanza di un metodo risolutivo o da limiti teorici dell’informatica e della logica matematica.
Un elaboratore esegue istruzioni definite e sequenziali. Se il problema non offre un metodo risolutivo (ad esempio, un algoritmo), non può essere risolto automaticamente.
- Esempio:
- La previsione precisa di un evento casuale, come il risultato di un lancio di moneta. Non esiste un algoritmo che possa determinare con certezza il risultato, poiché è intrinsecamente casuale.
Se un problema presenta infinite soluzioni e non è possibile restringere il campo di ricerca, il calcolatore non può completare il lavoro.
- Esempio:
- Trovare tutti i numeri primi. Poiché l'insieme dei numeri primi è infinito, il calcolatore potrebbe calcolare nuovi numeri primi indefinitamente, senza mai concludere.
Alcuni problemi non hanno un metodo noto o generale per trovare una soluzione, anche se questa potrebbe teoricamente esistere.
- Esempio:
- Determinare con certezza il numero di soluzioni di un'equazione di grado superiore al quarto non è possibile in tutti i casi, poiché non esistono formule generali per questo scopo.
Esistono problemi per i quali è stato dimostrato che non è possibile costruire un algoritmo risolutivo generale. Questi rientrano nella categoria dei problemi indecidibili, come definito nella teoria della computabilità.
- Esempio:
- Problema della terminazione (Halting Problem):
- Descrizione: Dato un programma e un input, determinare se il programma terminerà o andrà in loop infinito.
- Dimostrazione: Alan Turing ha dimostrato che non esiste un algoritmo generale che possa risolvere questo problema per tutti i programmi possibili.
- Problema della terminazione (Halting Problem):
Molti limiti derivano dal modello teorico della macchina di Turing, che rappresenta la base della computabilità.
- Problemi risolvibili: I problemi per i quali esiste un algoritmo, ovvero un procedimento definito che termina in un tempo finito.
- Problemi non risolvibili: Quelli per cui non è possibile definire un algoritmo che garantisca una risposta in ogni caso.
Un calcolatore può affrontare solo problemi:
- Con una descrizione chiara e completa.
- Per i quali esiste un metodo risolutivo (algoritmo).
- Che rientrano nei limiti della computabilità.
I problemi senza metodo risolutivo, con soluzioni infinite o dimostrati indecidibili restano irrisolvibili attraverso i mezzi informatici, anche teoricamente.
Un elaboratore è in grado di risolvere problemi che possono essere tradotti in istruzioni precise e sequenziali, basate su dati e metodi ben definiti. Questi problemi spaziano da operazioni semplici ad attività complesse e sono rappresentativi di molte applicazioni informatiche nella vita quotidiana.
- Gli elaboratori possono generare documenti standardizzati (certificati, report, fatture) a partire da modelli predefiniti e dati inseriti in archivi o database.
- Esempio:
- Emissione di report finanziari mensili.
- Generazione di certificati accademici con dati degli studenti.
- Gli elaboratori gestiscono operazioni bancarie online, come trasferimenti di denaro, pagamenti e controllo dei saldi.
- Esempio:
- Effettuare un bonifico o pagare una bolletta tramite l'app della banca.
- Sistemi di prenotazione automatizzati per voli, treni, hotel o eventi, che incrociano disponibilità e richieste degli utenti.
- Esempio:
- Prenotare un volo aereo confrontando prezzi su più piattaforme.
- Calcoli matematici semplici o complessi possono essere eseguiti con estrema velocità e precisione.
- Esempio:
- Calcolare interessi su un capitale.
- Risolvere equazioni matematiche.
- L'elaboratore può ordinare insiemi di numeri, parole o oggetti secondo criteri specifici.
- Esempio:
- Ordinare un elenco di nomi alfabeticamente.
- Ordinare le vendite mensili di un'azienda in ordine decrescente.
- Gli elaboratori possono trovare elementi comuni tra due o più insiemi di dati.
- Esempio:
- Identificare clienti che hanno acquistato più di un prodotto specifico.
- Attraverso algoritmi, l'elaboratore può analizzare dati e calcolare metriche utili.
- Esempio:
- Determinare lo stipendio medio dei dipendenti di un'azienda basandosi su un database.
- Problemi matematici come equazioni lineari possono essere facilmente automatizzati.
- Esempio:
- Dati
aeb, risolvere l'equazioneax + b = 0con il risultatox = -b/a.
- Dati
- Gli elaboratori gestiscono sistemi complessi per:
- Fornire contenuti multimediali.
- Simulare mondi virtuali nei videogiochi.
- Connettere persone sui social network.
- Esempio:
- Streaming di video e musica.
- Giocare a un videogioco online.
Gli elaboratori possono risolvere una vasta gamma di problemi in numerosi ambiti:
- Sanità: Analisi di dati medici per diagnosi assistite.
- Educazione: Piattaforme di e-learning.
- Business: Automazione dei processi aziendali.
- Ricerca scientifica: Simulazioni complesse in fisica, chimica o biologia.
Gli elaboratori eccellono nel risolvere problemi ben definiti e strutturati, dove i dati iniziali e il metodo per ottenere i risultati finali sono chiari. Questo li rende strumenti indispensabili per velocità, precisione e affidabilità in una vasta gamma di applicazioni.