Skip to content

Latest commit

 

History

History
147 lines (96 loc) · 6.83 KB

01.Array-Binary-Search-01.md

File metadata and controls

147 lines (96 loc) · 6.83 KB
Raw

1. 二分查找算法介绍

1.1 二分查找算法简介

二分查找算法（Binary Search Algorithm）：也叫做折半查找算法、对数查找算法，是一种用于在有序数组中查找特定元素的高效搜索算法。

二分查找的基本算法思想为：通过确定目标元素所在的区间范围，反复将查找范围减半，直到找到元素或找不到该元素为止。

1.2 二分查找算法步骤

以下是二分查找算法的基本步骤：

  1. 初始化：首先，确定要查找的有序数据集合。可以是一个数组或列表，确保其中的元素按照升序或者降序排列。

  2. 确定查找范围：将整个有序数组集合的查找范围确定为整个数组范围区间，即左边界 $left$ 和右边界 $right$。

  3. 计算中间元素：根据 $mid = \lfloor (left + right) / 2 \rfloor$ 计算出中间元素下标位置 $mid$。

  4. 比较中间元素：将目标元素 $target$ 与中间元素 $nums[mid]$ 进行比较：

    1. 如果 $target == nums[mid]$，说明找到 $target$，因此返回中间元素的下标位置 $mid$。
    2. 如果 $target < nums[mid]$，说明目标元素在左半部分（$[left, mid - 1]$），更新右边界为中间元素的前一个位置，即 $right = mid - 1$。
    3. 如果 $target > nums[mid]$，说明目标元素在右半部分（$[mid + 1, right]$），更新左边界为中间元素的后一个位置，即 $left = mid + 1$。

  5. 重复步骤 $3 \sim 4$，直到找到目标元素时返回中间元素下标位置，或者查找范围缩小为空（左边界大于右边界），表示目标元素不存在，此时返回 $-1$。

举个例子来说，以在有序数组 $[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]$ 中查找目标元素 $6$ 来说，使用二分查找算法的步骤如下：

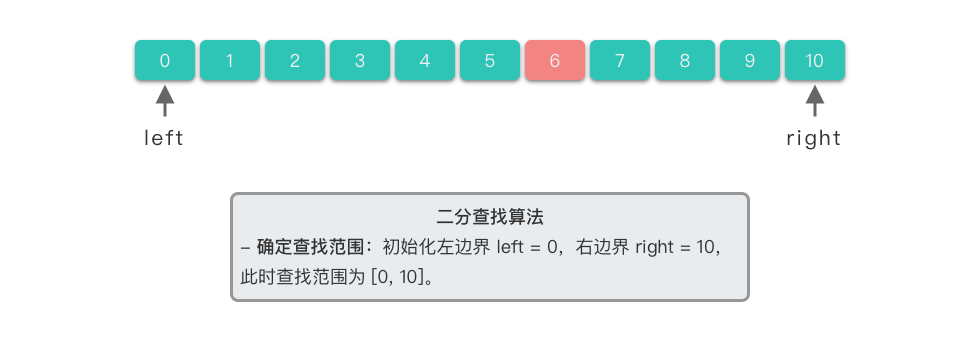
  1. 确定查找范围：初始时左边界 $left = 0$（数组的起始位置），$right = 10$（数组的末尾位置）。此时查找范围为 $[0, 10]$。
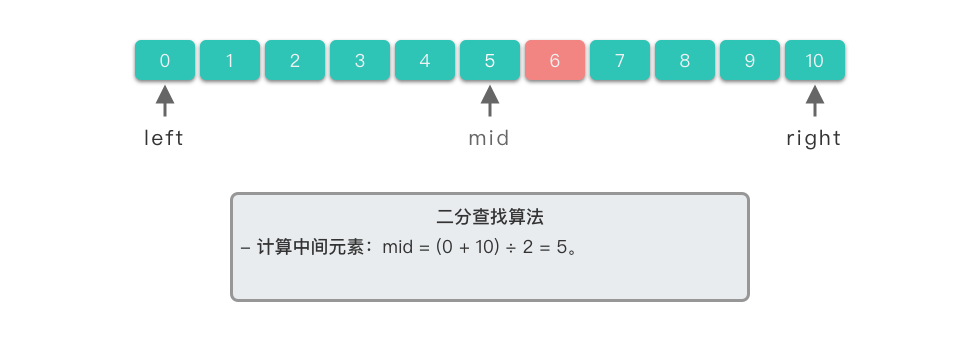
  2. 计算中间元素：中间元素下标位置 $mid = (0 + 10) \div 2 = 5$，对应元素为 $nums[5] == 5$。
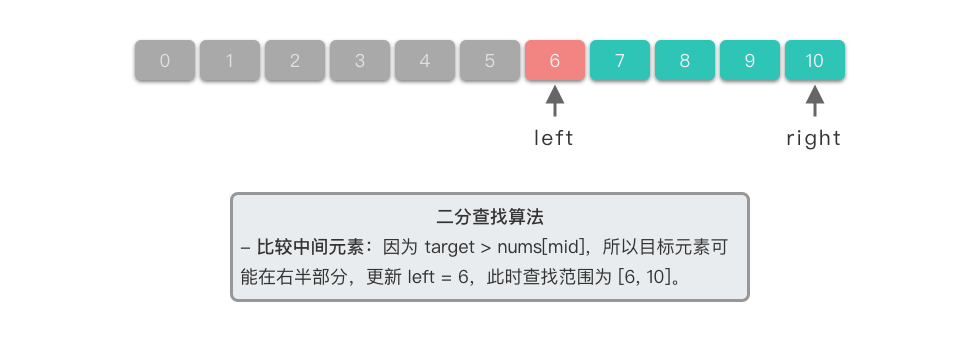
  3. 比较中间元素：因为 $6 > nums[5]$，所以目标元素可能在右半部分，更新左边界为中间元素的后一个位置，即 $left = 6$。此时查找范围为 $[6, 10]$。
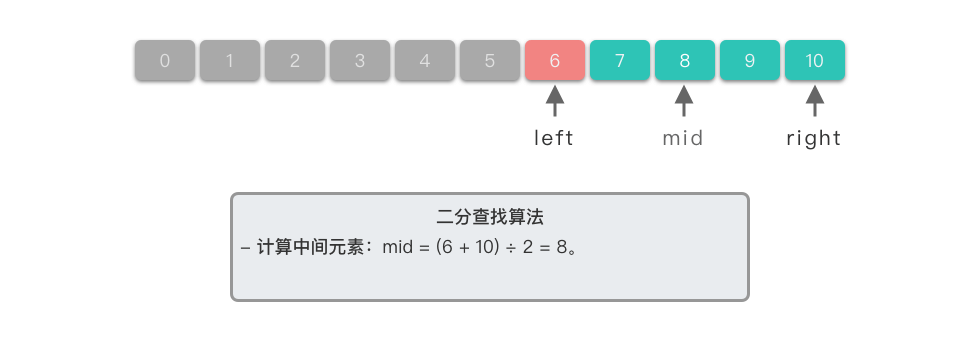
  4. 计算中间元素：中间元素下标位置 $mid = (6 + 10) \div 2 = 8$，对应元素为 $nums[8] == 8$。
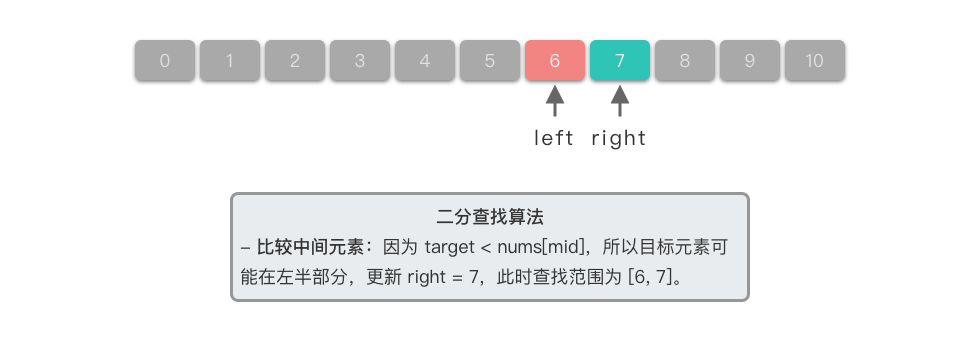
  5. 比较中间元素：因为 $6 < nums[8]$，所以目标元素可能在左半部分，更新右边界为中间元素的前一个位置，即 $right = 7$。此时查找范围为 $[6, 7]$。
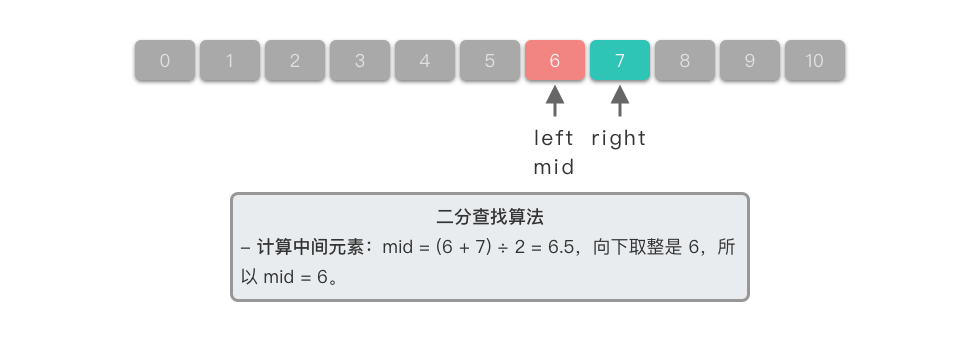
  6. 计算中间元素：中间元素下标位置 $mid = (6 + 7) \div 2 = 6$（向下取整），对应元素为 $nums[6] == 6$。
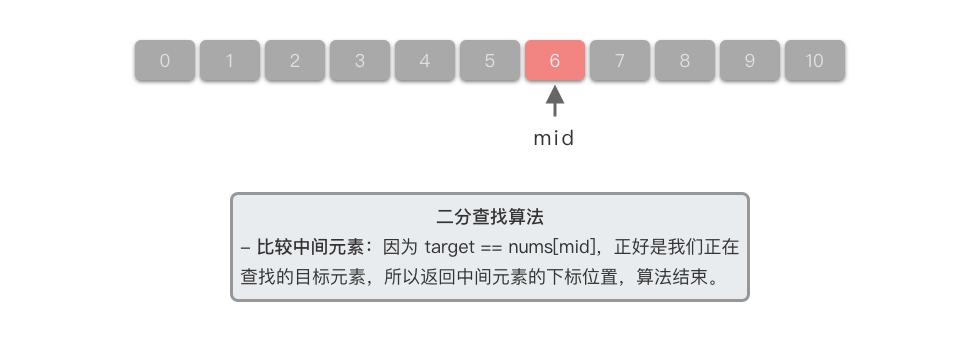
  7. 比较中间元素：因为 $6 == nums[6]$，正好是我们正在查找的目标元素，此时返回中间元素的下标位置，算法结束。

于是我们发现，对于一个长度为 $10$ 的有序数组，我们只进行了 $3$ 次查找就找到了目标元素。而如果是按照顺序依次遍历数组，则在最坏情况下，我们可能需要查找 $10$ 次才能找到目标元素。

::: tabs#BinarySearch

@tab <1>

二分查找算法 1

@tab <2>

二分查找算法 2

@tab <3>

二分查找算法 3

@tab <4>

二分查找算法 4

@tab <5>

二分查找算法 5

@tab <6>

二分查找算法 6

@tab <7>

二分查找算法 7

@tab <8>

二分查找算法 8

:::

1.2 二分查找算法思想

二分查找算法是经典的 「减而治之」 的思想。

这里的 「减」 是减少问题规模的意思，「治」 是解决问题的意思。「减」 和 「治」 结合起来的意思就是 「排除法解决问题」。即：每一次查找，排除掉一定不存在目标元素的区间，在剩下可能存在目标元素的区间中继续查找。

每一次通过一些条件判断，将待搜索的区间逐渐缩小，以达到「减少问题规模」的目的。而于问题的规模是有限的，经过有限次的查找，最终会查找到目标元素或者查找失败。

2. 简单二分查找

下面通过一个简单的例子来讲解下二分查找的思路和代码。

2.1 题目大意

描述：给定一个升序的数组 $nums$，和一个目标值 $target$。

要求：返回 $target$ 在数组中的位置，如果找不到，则返回 $-1$。

说明：

  • 你可以假设 $nums$ 中的所有元素是不重复的。
  • $n$ 将在 $[1, 10000]$ 之间。
  • $nums$ 的每个元素都将在 $[-9999, 9999]$之间。

示例：

输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4

输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1

2.2 解题思路

思路 1：二分查找

  1. 设定左右边界为数组两端，即 $left = 0$，$right = len(nums) - 1$，代表待查找区间为 $[left, right]$（左闭右闭区间）。
  2. 取两个节点中心位置 $mid$，先比较中心位置值 $nums[mid]$ 与目标值 $target$ 的大小。
    1. 如果 $target == nums[mid]$，则返回中心位置。
    2. 如果 $target &gt; nums[mid]$，则将左节点设置为 $mid + 1$，然后继续在右区间 $[mid + 1, right]$ 搜索。
    3. 如果 $target &lt; nums[mid]$，则将右节点设置为 $mid - 1$，然后继续在左区间 $[left, mid - 1]$ 搜索。
  3. 如果左边界大于右边界，查找范围缩小为空，说明目标元素不存在，此时返回 $-1$。

思路 1：代码

class Solution:
    def search(self, nums: List[int], target: int) -> int:
        left, right = 0, len(nums) - 1
        
        # 在区间 [left, right] 内查找 target
        while left <= right:
            # 取区间中间节点
            mid = (left + right) // 2
            # 如果找到目标值，则直接返回中心位置
            if nums[mid] == target:
                return mid
            # 如果 nums[mid] 小于目标值，则在 [mid + 1, right] 中继续搜索
            elif nums[mid] < target:
                left = mid + 1
            # 如果 nums[mid] 大于目标值，则在 [left, mid - 1] 中继续搜索
            else:
                right = mid - 1
        # 未搜索到元素，返回 -1
        return -1

思路 1：复杂度分析

  • 时间复杂度：$O(\log n)$。
  • 空间复杂度：$O(1)$。