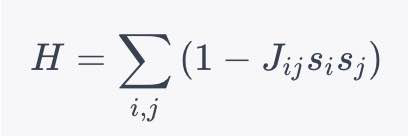Skip to content

Latest commit

 

History

History
284 lines (168 loc) · 11.1 KB

KeyTerms.md

File metadata and controls

284 lines (168 loc) · 11.1 KB

Super-node Concept The k-Concurrent Graph Partitioning algorithm is a method for partitioning a graph into k parts in parallel. The algorithm uses a super-node concept, where each vertex in the graph is represented by a logical qubit. The algorithm then uses a new formulation that requires a kn x kn QUBO, where n is the number of vertices in the graph. The result of the algorithm is that 1 of k qubits is set on for each vertex. This is similar to the graph coloring problem, and is useful for graph partitioning and community detection.k-Concurrent Graph Partitioning - Multiple parts in parallel

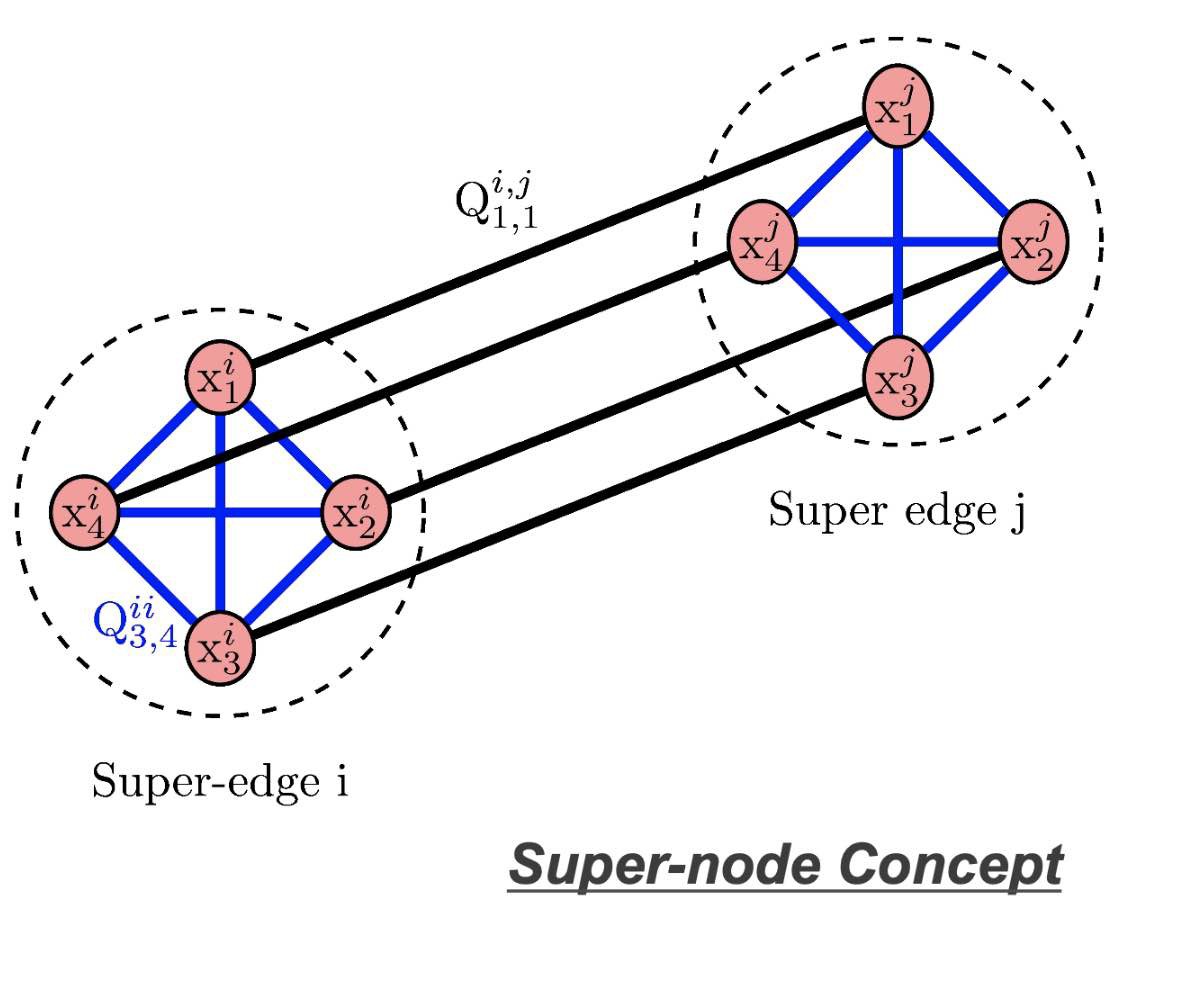
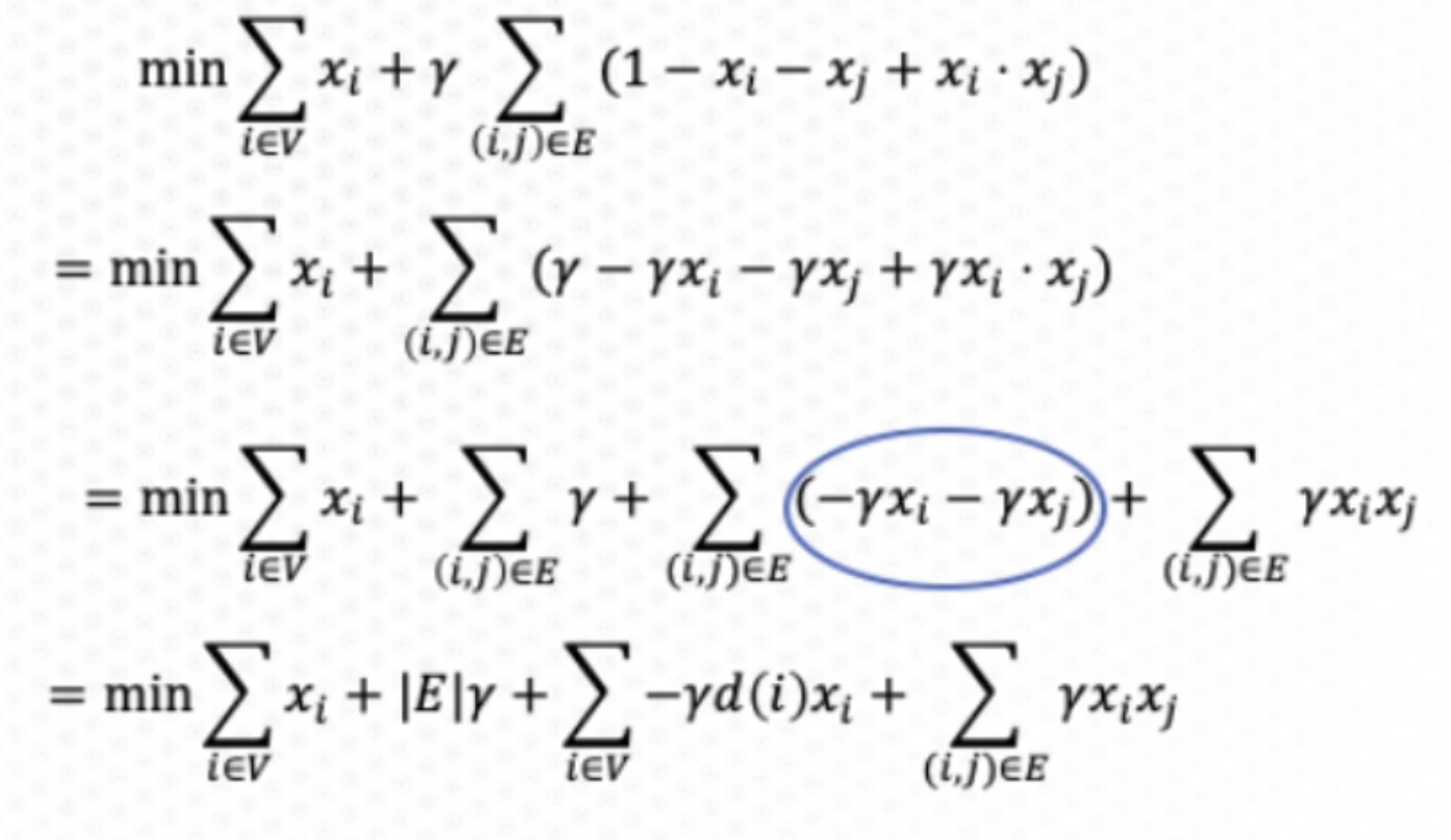
  • Partition into $k$ parts in parallel
  • Uses super-node concept
  • Unary embedding
  • k logical qubits per vertex
  • New formulation requires a kn x kn QUBO
  • Results in 1 of k qubits set on for each vertex
  • Similar to graph coloring problem
  • Useful for graph partitioning and community detection
Constraint Penalty Function
$x+y \leq 1$ $x \cdot y$
$x+y \geq 1$ $1-x-y+x \cdot y$
$x+y=1$ $1-x-y+2 \cdot x \cdot y$
$x \leq y$ $x-x \cdot y$
$x+y+z \leq 1$ $x \cdot y+x \cdot z+y \cdot z$
$x=y$ $x+y-2 \cdot x \cdot y$
Concepts Related terms
Binary Quadratic Models BQM, Ising, QUBO
$\begin{array}{l}\text { Constrained Quadratic } \\text { Models }\end{array}$ CQM, constrained quadratic model
Constraint Satisfaction CSP, binary CSP
Discrete Quadratic Models DQM, discrete quadratic model
Hybrid quantum-classical hybrid, Leap's hybrid solvers, hybrid workflows
Minor-Embedding $\begin{array}{l}\text { embedding, mapping logical variables to physical qubits, chains, chain } \\text { strength }\end{array}$
Penalty Models Penalty Models
Quadratic Models Quadratic Models
QPU Topology Chimera, Pegasus
Samplers and Composites solver
Solutions samples, sampleset, probabilistic, energy
Variables binary, discrete, integer, real variables

DiVincenzo's

electromagnetic wave propagating through a chain of identical qubits placed in a transmission line, and considered as an effective medium.

circuit formalism, ${ }^{42}$

node

"flux" $\Phi_n$,

time derivative

node potential (in CGS units)

CGS units

Lumped element circuit

ID quantum metamaterial:

chain of flux qubits

transmission line

binary quadratic model BQM A collection of binary-valued variables (variables that can be assigned two values, for example $-1,1$ ) with associated linear and quadratic biases. Sometimes referred to in other tools as a problem. See a fuller description under Binary Quadratic Models.

Chain One or more nodes or qubits in a target graph that represent a single variable in the source graph. See embedding. See a fuller description under Minor-Embedding.Chain and Minor-Embedding In the context of quantum computing, particularly with D-Wave systems, a chain refers to a collection of physical qubits on the quantum processing unit (QPU) that together represent a single logical variable from the problem being solved. Minor-embedding is the process of mapping these logical variables to these chains on the QPU.

Chain length The number of qubits in a Chain. See a fuller description under Minor-Embedding.Chain length refers to the number of physical qubits in a chain that represents a single logical variable in your problem formulation.

Chain strength Magnitude of the negative quadratic bias applied between variables to form a chain. See a fuller description under Minor-Embedding. Chain strength refers to the magnitude of the negative quadratic bias applied between qubits in a chain to enforce that they take on the same value during the quantum annealing process.

Chimera A D-Wave QPU is a lattice of interconnected qubits. While some qubits connect to others via couplers, D-Wave QPUs are not fully connected. For D-Wave 2000Q QPUs, the qubits interconnect in an architecture known as Chimera. See a fuller description under QPU Topology. See also Pegasus and Zephyr. The Chimera topology is one of the qubit interconnection architectures featured in D-Wave systems, specifically in the D-Wave 2000 Q QPUs.

The Hamiltonian is the heart of the problem description in quantum systems, encapsulating the energy of the system in terms of its state variables and interactions. D-Wave systems are designed to solve optimization and sampling problems by minimizing a particular Hamiltonian.

Objective function A mathematical expression of the energy of a system as a function of binary variables representing the qubits.

Math:

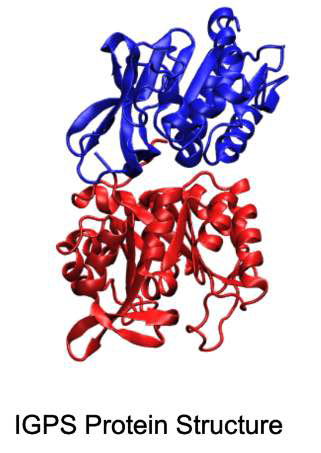
Clustering for Identifying Communities in Bio-Systems: A Mathematical and Pythonic Perspective

Overview

In this project, we explore the concept of community detection within bio-systems, with a specific focus on the enzyme IGPS found in bacteria. We use both classical algorithms such as Girvan-Newman and quantum algorithms using D-Wave's qbsolv to approach this optimization problem.

Mathematical Concepts

1. Mutual Information

Mutual Information ( \mathbf{r}_{ij}^{MI} ) between two residues ( \mathbf{x}_i ) and ( \mathbf{x}_j ) in the enzyme is calculated using a function ( g ) as follows:

[ \mathbf{r}_{ij}^{MI} = g\left(\mathbf{I}[\mathbf{x}_i, \mathbf{x}_j]\right) ]

2. Modularity Matrix

The modularity matrix ( Q ) is an essential tool for detecting communities within the network. It is defined as:

[ Q = B - \gamma A ]

Where:

  • ( B ) is the adjacency matrix
  • ( A ) is the degree matrix
  • ( \gamma ) is a resolution parameter

Python3 Code Implementation

To get started, install the required Python packages:

pip install numpy dwave-ocean-sdk

Here's the Python3 code that demonstrates the community detection approach:

import numpy as np
from dwave.system import DWaveSampler, EmbeddingComposite
from dwave_qbsolv import QBSolv

# Generate a correlation matrix (This is a mock-up for demonstration)
n = 454  # Number of residues in IGPS
C = np.random.rand(n, n)

# Calculate modularity matrix
gamma = 1.0
A = np.sum(C, axis=0)
Q = C - gamma * np.outer(A, A) / np.sum(A)

# Prepare for qbsolv
Q_dict = {(i, j): Q[i, j] for i in range(n) for j in range(n)}

# Initialize D-Wave parameters
sampler = EmbeddingComposite(DWaveSampler())
response = QBSolv().sample_qubo(Q_dict, solver=sampler, num_repeats=10)

# Extract communities
best_sample = response.first.sample
communities = {node: state for node, state in best_sample.items()}

Exploring Signed Social Networks with D-Wave: Challenges and Insights

Overview

The study aims to explore the computational efficacy of D-Wave in calculating structural balance in signed social networks. We conducted experiments on fully-connected graphs and compared the performance of D-Wave against a simulator.

Challenges

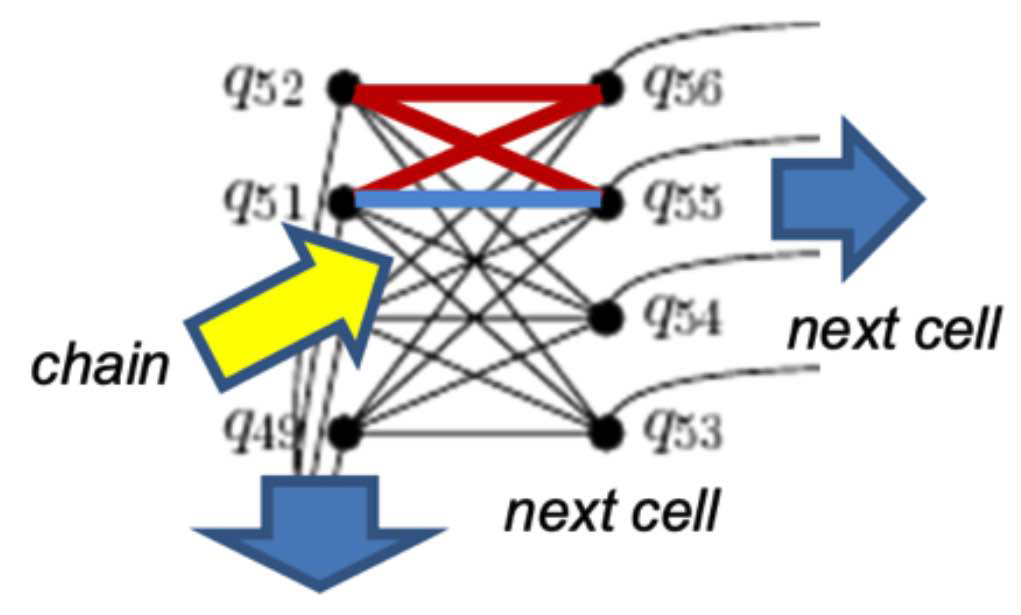
  1. Topology Mismatch: Arbitrary networks often do not align with D-Wave's native topology, complicating the mapping process. Even simple structures like triangles pose challenges.
  2. Embedding Complexity: Creating the desired topology by chaining nodes together, a process called "embedding," is NP-hard.
  3. Hardware Limitations: Given the current D-Wave machine topology and available qubits, the upper limit for fully-connected, simulated nodes is approximately 49.
  4. Overhead Costs: A significant portion of the execution time on D-Wave is spent on communication and initialization, overshadowing the D-Wave's fast annealing time of 20 microseconds.

Mathematical Formulation

The Ising model equivalent to this problem is governed by the Hamiltonian:

[ H = \sum_{i, j} \left( 1 - J_{ij} s_i s_j \right) ]

Where ( J_{ij} ) and ( s_i ) are as described earlier.

Python Code Snippet

Given the challenges, it's crucial to optimize the D-Wave code as much as possible. Here's a code snippet that minimizes overhead:

from dwave.system import DWaveSampler, EmbeddingComposite

# Predefined J matrix (mock example)
J = {(0, 1): 1, (1, 2): -1, (0, 2): -1}

# Initialize D-Wave sampler
sampler = DWaveSampler()
embedded_sampler = EmbeddingComposite(sampler)

# Sample with minimal overhead
params = {'num_reads': 1000, 'annealing_time': 20}  # Annealing time in microseconds
response = embedded_sampler.sample_ising({}, J, **params)

# Extract optimal assignment
best_sample = response.first.sample
optimal_assignment = {node: 'Positive' if state == 1 else 'Negative' for node, state in best_sample.items()}

print("Optimal Assignment:", optimal_assignment)

Citations /References:

Zagoskin, A. M. (2010). Why quantum engineering?. Low Temperature Physics, 36(10), 911-914. https://doi.org/10.1063/1.3515522

D-Wave Systems

Los Alomos National Lab