[[toc]]
[toc]
😶🌫️go语言官方编程指南:https://pkg.go.dev/std
go语言的官方文档学习笔记很全,推荐去官网学习
😶🌫️我的学习笔记:github: https://github.com/3293172751/golang-rearn
区块链技术(也称之为分布式账本技术),是一种互联网数据库技术,其特点是去中心化,公开透明,让每一个人均可参与的数据库记录
❤️💕💕关于区块链技术,可以关注我,共同学习更多的区块链技术。博客http://nsddd.top
©️®️ 排序和查找是一个大的方向,我准备结合数据结构,以python,C/C++为辅助,Golang为主线进行
✍️ 排序(sorting)是指将数据元素(或记录)的任意序列,重新排列成一个按照关键字的有序序列(递增或递减)的序列过程称为排序
排序分为内部排序和外部排序,也分为稳定排序和不稳定排序
内部排序是指整个排序过程完全在内存中进行,包括(交换式排序、选择式排序和插入式排序)
由于数据量太大,内存无法容纳全部数据,排序需要借助外部存储设备才能完成,包括**(合并排序法和直接合并排序法)**
- 稳定排序:排序前后两个相等的数相对位置不变,则算法稳定
- 非稳定排序:排序前后两个相等的数相对位置发生了变化,则算法不稳定
1、如果只是简单的进行数字的排序,那么稳定性将毫无意义。
2、如果排序的内容仅仅是一个复杂对象的某一个数字属性,那么稳定性依旧将毫无意义(所谓的交换操作的开销已经算在算法的开销内了,如果嫌弃这种开销,不如换算法好了?)
3、如果要排序的内容是一个复杂对象的多个数字属性,但是其原本的初始顺序毫无意义,那么稳定性依旧将毫无意义。
4、除非要排序的内容是一个复杂对象的多个数字属性,且其原本的初始顺序存在意义,那么我们需要在二次排序的基础上保持原有排序的意义,才需要使用到稳定性的算法,例如要排序的内容是一组原本按照价格高低排序的对象,如今需要按照销量高低排序,使用稳定性算法,可以使得想同销量的对象依旧保持着价格高低的排序展现,只有销量不同的才会重新排序。(当然,如果需求不需要保持初始的排序意义,那么使用稳定性算法依旧将毫无意义)
✍️交换排序的基本方法是:通过两两比较待排序记录的关键字,若有不满足次序要求的一对数据则交换,直到全部满足位置
冒泡排序(Bubble Sort)也是一种简单直观的排序算法。它重复地走访过要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢"浮"到数列的顶端。
先用简单的python实现
def bubbleSort(arr):
n = len(arr)
# 遍历所有数组元素
for i in range(n):
exchange = 0 #看本次是否有交换
# Last i elements are already in place
for j in range(0, n-i-1):
if arr[j] > arr[j+1] :
arr[j], arr[j+1] = arr[j+1], arr[j] //直接交换,无需中间变量
exchange = 1
if exchange == 0:
return arr
arr = [64, 34, 25, 12, 22, 11, 90]
bubbleSort(arr)
print ("排序后的数组:")
for i in range(len(arr)):
print ("%d" %arr[i]),编译:
def bubble_sort(array):
for i in range(1, len(array)):
a=0
for j in range(0, len(array)-i):
if array[j] > array[j+1]:
array[j], array[j+1] = array[j+1], array[j]
a=1
if a==0:
return array
return array
if __name__ == '__main__':
array = [10, 17, 50, 7, 30, 24, 27, 45, 15, 5, 36, 21]
print(bubble_sort(array))编译:
思想:
设定了一个辅助,一旦发现了某一趟没有要进行交换的操作,就立刻终止程序,此时可以减少时间复杂度
下面是Golang的冒泡排序算法:
package main
import (
"fmt"
"time"
)
func main() {
values := []int{4, 93, 84, 85, 80, 37, 81, 93, 27,12}
start := time.Now().UnixNano()
fmt.Println(values) //打印输出当前的切片
BubbleAsort(values) //交换函数,values[i]>values[j] 从小到大
BubbleZsort(values) //交换函数,values[i]<values[j] 从大到小
end := time.Now().UnixNano()
fmt.Println("代码执行的时间为:",end-start)
}
func BubbleAsort(values []int) {
for i := 0; i < len(values)-1; i++ {
a := 0
for j := i+1; j < len(values); j++ {
if values[i]>values[j]{
values[i],values[j] = values[j],values[i] //和python一样直接交换
a = 1
}
}
if a ==0{
return
}
}
fmt.Println(values)
}
func BubbleZsort(values []int) {
a := 0
for i := 0; i < len(values)-1; i++ {
for j := i+1; j < len(values); j++ {
if values[i]<values[j]{
values[i],values[j] = values[j],values[i]
a = 1
}
}
if a ==0{
return
}
}
fmt.Println(values)
}我们可以用Golang来统计下使用a和不使用a代码执行时间
start := time.Now().UnixNano()
fmt.Println(values)
BubbleAsort(values)
BubbleZsort(values)
end := time.Now().UnixNano()
fmt.Println("代码执行的时间为:",end-start)根据上下的大数据分析,可见代码的执行时间确实提升了😂😂😂
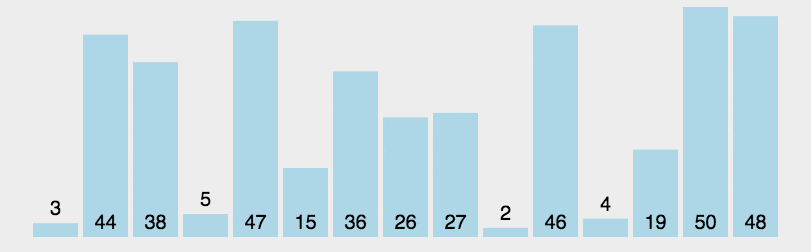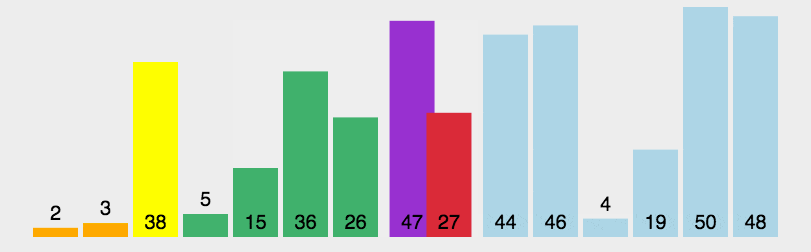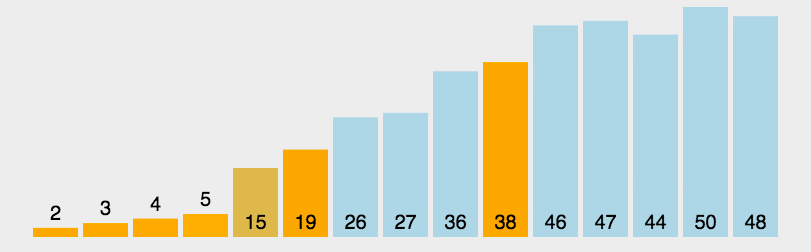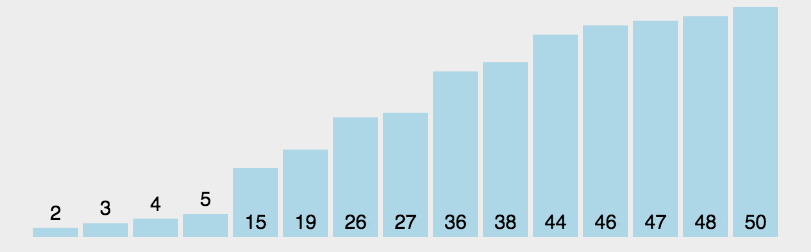
快速排序由于排序效率在同为O(N*logN)的几种排序方法中效率较高,因此经常被采用,再加上快速排序思想----分治法也确实实用,因此很多软件公司的笔试面试,包括像腾讯,微软等知名IT公司都喜欢考这个,还有大大小的程序方面的考试如软考,考研中也常常出现快速排序的身影。
总的说来,要直接默写出快速排序还是有一定难度的,因为本人就自己的理解对快速排序作了下白话解释,希望对大家理解有帮助,达到快速排序,快速搞定。
快速排序是C.R.A.Hoare于1962年提出的一种划分交换排序。它采用了一种分治的策略,通常称其为分治法(Divide-and-ConquerMethod)。
该方法的基本思想是:
-
1.先从数列中取出一个数作为基准数。
-
2.分区过程,将比这个数大的数全放到它的右边,小于或等于它的数全放到它的左边。
-
3.再对左右区间重复第二步,直到各区间只有一个数。
-
-
虽然快速排序称为分治法,但分治法这三个字显然无法很好的概括快速排序的全部步骤。因此我的对快速排序作了进一步的说明:挖坑填数+分治法:
-
先来看实例吧,定义下面再给出(最好能用自己的话来总结定义,这样对实现代码会有帮助)。
-
以一个数组作为示例,取区间第一个数为基准数。
-
0 1 2 3 4 5 6 7 8 9 72 6 57 88 60 42 83 73 48 85 -
初始时,i = 0; j = 9; X = a[i] = 72
-
由于已经将 a[0] 中的数保存到 X 中,可以理解成在数组 a[0] 上挖了个坑,可以将其它数据填充到这来。
-
从j开始向前找一个比X小或等于X的数。当j=8,符合条件,将a[8]挖出再填到上一个坑a[0]中。a[0]=a[8]; i++; 这样一个坑a[0]就被搞定了,但又形成了一个新坑a[8],这怎么办了?简单,再找数字来填a[8]这个坑。这次从i开始向后找一个大于X的数,当i=3,符合条件,将a[3]挖出再填到上一个坑中a[8]=a[3]; j--;
-
数组变为:
-
0 1 2 3 4 5 6 7 8 9 48 6 57 88 60 42 83 73 88 85 -
i = 3; j = 7; X=72
-
再重复上面的步骤,先从后向前找,再从前向后找。
-
从j开始向前找,当j=5,符合条件,将a[5]挖出填到上一个坑中,a[3] = a[5]; i++;
-
从i开始向后找,当i=5时,由于i==j退出。
-
此时,i = j = 5,而a[5]刚好又是上次挖的坑,因此将X填入a[5]。
-
数组变为:
-
0 1 2 3 4 5 6 7 8 9 48 6 57 42 60 72 83 73 88 85 -
可以看出a[5]前面的数字都小于它,a[5]后面的数字都大于它。因此再对a[0…4]和a[6…9]这二个子区间重复上述步骤就可以了。
-
对挖坑填数进行总结:
-
- 1.i =L; j = R; 将基准数挖出形成第一个坑a[i]。
- 2.j--由后向前找比它小的数,找到后挖出此数填前一个坑a[i]中。
- 3.i++由前向后找比它大的数,找到后也挖出此数填到前一个坑a[j]中。
- 4.再重复执行2,3二步,直到i==j,将基准数填入a[i]中。
-
照着这个总结很容易实现挖坑填数的代码:
-
int AdjustArray(int s[], int l, int r) //返回调整后基准数的位置
{
int i = l, j = r;
int x = s[l]; //s[l]即s[i]就是第一个坑
while (i < j)
{
// 从右向左找小于x的数来填s[i]
while(i < j && s[j] >= x)
j--;
if(i < j)
{
s[i] = s[j]; //将s[j]填到s[i]中,s[j]就形成了一个新的坑
i++;
}
// 从左向右找大于或等于x的数来填s[j]
while(i < j && s[i] < x)
i++;
if(i < j)
{
s[j] = s[i]; //将s[i]填到s[j]中,s[i]就形成了一个新的坑
j--;
}
}
//退出时,i等于j。将x填到这个坑中。
s[i] = x;
return i;
}再写分治法的代码:
void quick_sort1(int s[], int l, int r)
{
if (l < r)
{
int i = AdjustArray(s, l, r);//先成挖坑填数法调整s[]
quick_sort1(s, l, i - 1); // 递归调用
quick_sort1(s, i + 1, r);
}
}//快速排序
void quick_sort(int s[], int l, int r)
{
if (l < r)
{
//Swap(s[l], s[(l + r) / 2]); //将中间的这个数和第一个数交换 参见注1
int i = l, j = r, x = s[l];
while (i < j)
{
while(i < j && s[j] >= x) // 从右向左找第一个小于x的数
j--;
if(i < j)
s[i++] = s[j];
while(i < j && s[i] < x) // 从左向右找第一个大于等于x的数
i++;
if(i < j)
s[j--] = s[i];
}
s[i] = x;
quick_sort(s, l, i - 1); // 递归调用
quick_sort(s, i + 1, r);
}
}def partition(arr,low,high):
i = ( low-1 ) # 最小元素索引
pivot = arr[high]
for j in range(low , high):
# 当前元素小于或等于 pivot
if arr[j] <= pivot:
i = i+1
arr[i],arr[j] = arr[j],arr[i]
arr[i+1],arr[high] = arr[high],arr[i+1]
return ( i+1 )
# arr[] --> 排序数组
# low --> 起始索引
# high --> 结束索引
# 快速排序函数
def quickSort(arr,low,high):
if low < high:
pi = partition(arr,low,high)
quickSort(arr, low, pi-1)
quickSort(arr, pi+1, high)
arr = [10, 7, 8, 9, 1, 5]
n = len(arr)
quickSort(arr,0,n-1)
print ("排序后的数组:")
for i in range(n):
print ("%d" %arr[i])执行以上代码输出结果为:
排序后的数组:
1
5
7
8
9
10
线性查找指按一定的顺序检查数组中每一个元素,直到找到所要寻找的特定值为止。
def search(arr, n, x):
for i in range (0, n):
if (arr[i] == x):
return i;
return -1;
# 在数组 arr 中查找字符 D
arr = [ 'A', 'B', 'C', 'D', 'E' ];
x = 'D';
n = len(arr);
result = search(arr, n, x)
if(result == -1):
print("元素不在数组中")
else:
print("元素在数组中的索引为", result);执行以上代码输出结果为:
元素在数组中的索引为 3
二分搜索是一种在有序数组中查找某一特定元素的搜索算法。搜索过程从数组的中间元素开始,如果中间元素正好是要查找的元素,则搜索过程结束;如果某一特定元素大于或者小于中间元素,则在数组大于或小于中间元素的那一半中查找,而且跟开始一样从中间元素开始比较。如果在某一步骤数组为空,则代表找不到。这种搜索算法每一次比较都使搜索范围缩小一半。
💡简单的一个案例如下:
# 返回 x 在 arr 中的索引,如果不存在返回 -1
def binarySearch (arr, l, r, x):
# 基本判断
if r >= l:
mid = int(l + (r - l)/2)
# 元素整好的中间位置
if arr[mid] == x:
return mid
# 元素小于中间位置的元素,只需要再比较左边的元素
elif arr[mid] > x:
return binarySearch(arr, l, mid-1, x)
# 元素大于中间位置的元素,只需要再比较右边的元素
else:
return binarySearch(arr, mid+1, r, x)
else:
# 不存在
return -1
# 测试数组
arr = [ 2, 3, 4, 10, 40 ]
x = 10
# 函数调用
result = binarySearch(arr, 0, len(arr)-1, x)
if result != -1:
print ("元素在数组中的索引为 %d" % result )
else:
print ("元素不在数组中")执行以上代码输出结果为:
元素在数组中的索引为 3
二分查找的前提是对一个==有序数组==
package main
import (
"fmt"
)
func BinaryFind(arr *[6]int,lef int,rig int,find int){
//数组是值传递,需要使用指针可以改变
//判断是否在数组的范围中
if lef > rig{
fmt.Println("找不到") //注意递归调用符合进站顺序,所以
return
}
middle := (lef + rig) /2
if(*arr)[middle] > find{
//大于要查找的数,此时应该向左边找
BinaryFind(arr,lef,middle - 1)
//注意,此时arr本身就是指针,所以不需要地址符
}else if (*arr)[middle] < find{
BinaryFind(arr,middle+1,rig)
}else{
//相等说明找到
fmt.Printf("找好了,下标为%v \n",middle)
}
}
func main(){
arr := [6]int{1,2,3,4,5,6,7,8,9}
BinaryFind(&arr,0,len(arr)-1,4)
}编译:
可以不传递地址,将数组转化为切片类型
::: tip sort包排序 升序排序如下:
intList := []int {2,4,3,5,7,6,9,1,0}
float8List := []float64 {2.3,1.4,1.5}
stringList := []string{"c","d","e","a","b"}
sort.Ints(intList)
sort.Float64s(float8List)
sort.Strings(stringList)sort包可以使用sort.Reverse(slice)来调换slice.Interface.Less,也就是比较函数,所以,int、float64、string的逆序排序函数可以这么写:
intList := []int {2,4,3,5,7,6,9,1,0}
float8List := []float64 {2.3,1.4,1.5}
stringList := []string{"c","d","e","a","b"}
sort.Sort(sort.Reverse(sort.IntSlice(intList)))
sort.Sort(sort.Reverse(sort.IntSlice(float8List)))
sort.Sort(sort.Reverse(sort.IntSlice(intList))):::
-
✴️版权声明 © :本书所有内容遵循CC-BY-SA 3.0协议(署名-相同方式共享)©