|
4 | 4 |
|
5 | 5 | A utility that can use 18 kinds of curve algorithm. |
6 | 6 |
|
7 | | -# Version |
| 7 | +## Version |
8 | 8 |
|
9 | | -- Unity 2017.3.0f3 |
| 9 | +- Unity 2018.3.0f2 |
10 | 10 |
|
11 | | -# Install |
12 | | - |
13 | | -1. Go to the following page and download "UnityCurveUtils.unitypackage". |
14 | | -https://github.com/baba-s/unity-curve-utils/blob/master/UnityCurveUtils.unitypackage?raw=true |
15 | | -2. Import the downloaded "UnityCurveUtils.unitypackage" into the Unity project. |
16 | | - |
17 | | -# Example |
| 11 | +## Example |
18 | 12 |
|
19 | 13 |  |
20 | 14 |
|
21 | 15 | An example of use of each curve algorithm is stored in "Example" folder. |
22 | 16 |
|
23 | | -# Algorithm list |
| 17 | +## Algorithm list |
24 | 18 |
|
25 | | -## B-Spline curve |
| 19 | +### B-Spline curve |
26 | 20 |
|
27 | 21 | 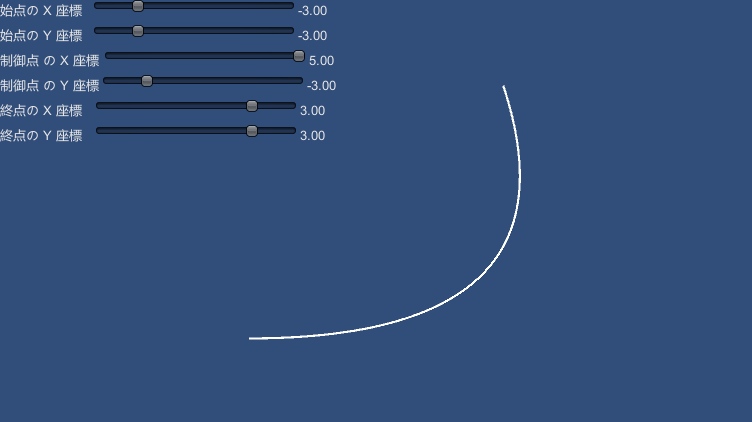 |
28 | 22 |
|
29 | 23 | ```cs |
30 | 24 | var point = UnityCurveUtils.B_SplineCurve( x1, y1, x2, y2, x3, y3, t ); |
31 | 25 | ``` |
32 | 26 |
|
33 | | -## Bezier curve |
| 27 | +### Bezier curve |
34 | 28 |
|
35 | 29 |  |
36 | 30 |
|
37 | 31 | ```cs |
38 | 32 | var point = UnityCurveUtils.BezierCurve( x1, y1, x2, y2, x3, y3, x4, y4, t ); |
39 | 33 | ``` |
40 | 34 |
|
41 | | -## Hyperbolic spiral |
| 35 | +### Hyperbolic spiral |
42 | 36 |
|
43 | 37 |  |
44 | 38 |
|
45 | 39 | ```cs |
46 | 40 | var point = UnityCurveUtils.HyperbolicSpiral( a, c theta ); |
47 | 41 | ``` |
48 | 42 |
|
49 | | -## Witch of agnesi |
| 43 | +### Witch of agnesi |
50 | 44 |
|
51 | 45 |  |
52 | 46 |
|
53 | 47 | ```cs |
54 | 48 | var point = UnityCurveUtils.WitchOfAgnesi( a, theta ); |
55 | 49 | ``` |
56 | 50 |
|
57 | | -## Folium of descartes |
| 51 | +### Folium of descartes |
58 | 52 |
|
59 | 53 |  |
60 | 54 |
|
61 | 55 | ```cs |
62 | 56 | var point = UnityCurveUtils.FoliumOfDescartes( a, theta ); |
63 | 57 | ``` |
64 | 58 |
|
65 | | -## Ellipse |
| 59 | +### Ellipse |
66 | 60 |
|
67 | 61 |  |
68 | 62 |
|
69 | 63 | ```cs |
70 | 64 | var point = UnityCurveUtils.Ellipse( a, b, theta ); |
71 | 65 | ``` |
72 | 66 |
|
73 | | -## Hyperbola |
| 67 | +### Hyperbola |
74 | 68 |
|
75 | 69 |  |
76 | 70 |
|
77 | 71 | ```cs |
78 | 72 | var point = UnityCurveUtils.Hyperbola( a, b, theta ); |
79 | 73 | ``` |
80 | 74 |
|
81 | | -## Involute of circle |
| 75 | +### Involute of circle |
82 | 76 |
|
83 | 77 |  |
84 | 78 |
|
85 | 79 | ```cs |
86 | 80 | var point = UnityCurveUtils.InvoluteOfCircle( a, theta ); |
87 | 81 | ``` |
88 | 82 |
|
89 | | -## Strophoid |
| 83 | +### Strophoid |
90 | 84 |
|
91 | 85 |  |
92 | 86 |
|
93 | 87 | ```cs |
94 | 88 | var point = UnityCurveUtils.Strophoid( a, theta ); |
95 | 89 | ``` |
96 | 90 |
|
97 | | -## Conchoid |
| 91 | +### Conchoid |
98 | 92 |
|
99 | 93 |  |
100 | 94 |
|
101 | 95 | ```cs |
102 | 96 | var point = UnityCurveUtils.Conchoid( a, l, theta ); |
103 | 97 | ``` |
104 | 98 |
|
105 | | -## Cissoid |
| 99 | +### Cissoid |
106 | 100 |
|
107 | 101 |  |
108 | 102 |
|
109 | 103 | ```cs |
110 | 104 | var point = UnityCurveUtils.Cissoid( a, theta ); |
111 | 105 | ``` |
112 | 106 |
|
113 | | -## Lissajous curve |
| 107 | +### Lissajous curve |
114 | 108 |
|
115 | 109 |  |
116 | 110 |
|
117 | 111 | ```cs |
118 | 112 | var point = UnityCurveUtils.LissajousCurve( A, B, a, b, delta, theta ); |
119 | 113 | ``` |
120 | 114 |
|
121 | | -## Trochoid |
| 115 | +### Trochoid |
122 | 116 |
|
123 | 117 | 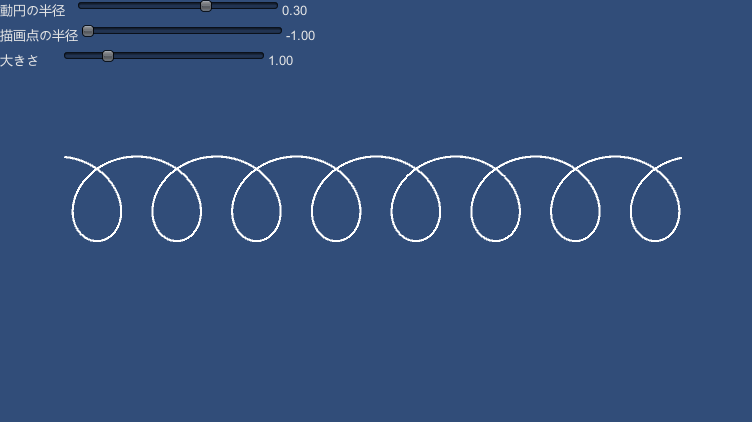 |
124 | 118 |
|
125 | 119 | ```cs |
126 | 120 | var point = UnityCurveUtils.Trochoid( rm, theta, rd ); |
127 | 121 | ``` |
128 | 122 |
|
129 | | -## Epitrocoid |
| 123 | +### Epitrocoid |
130 | 124 |
|
131 | 125 | 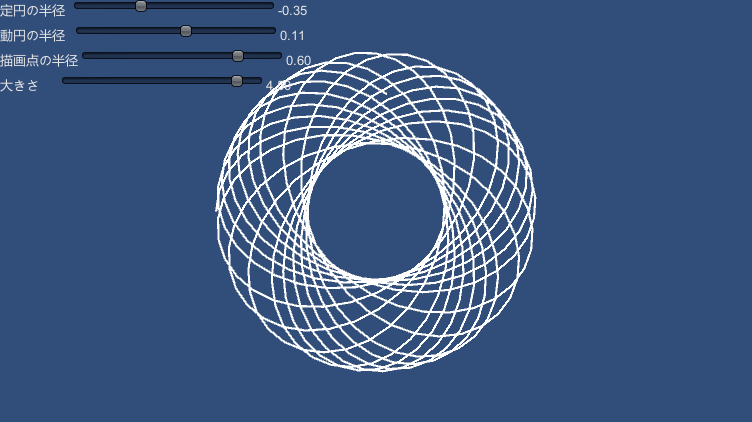 |
132 | 126 |
|
133 | 127 | ```cs |
134 | 128 | var point = UnityCurveUtils.Epitrocoid( rc, rm, theta, rd ); |
135 | 129 | ``` |
136 | 130 |
|
137 | | -## Hypetrocoid |
| 131 | +### Hypetrocoid |
138 | 132 |
|
139 | 133 | 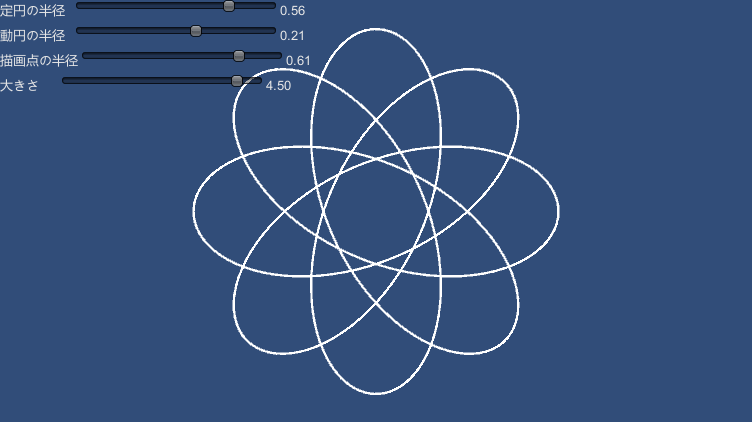 |
140 | 134 |
|
141 | 135 | ```cs |
142 | 136 | var point = UnityCurveUtils.Hypetrocoid( rc, rm, theta, rd ); |
143 | 137 | ``` |
144 | 138 |
|
145 | | -## Cycloid |
| 139 | +### Cycloid |
146 | 140 |
|
147 | 141 |  |
148 | 142 |
|
149 | 143 | ```cs |
150 | 144 | var point = UnityCurveUtils.Cycloid( rm, theta ); |
151 | 145 | ``` |
152 | 146 |
|
153 | | -## Epicycloid |
| 147 | +### Epicycloid |
154 | 148 |
|
155 | 149 |  |
156 | 150 |
|
157 | 151 | ```cs |
158 | 152 | var point = UnityCurveUtils.Epicycloid( rm, rd, theta ); |
159 | 153 | ``` |
160 | 154 |
|
161 | | -## Hypocycloid |
| 155 | +### Hypocycloid |
162 | 156 |
|
163 | 157 |  |
164 | 158 |
|
|
0 commit comments