diff --git a/presentaciones/pwl_mecanica_cuantica/pwl-30-ene-2020/introduccion_a_mc.ipynb b/presentaciones/pwl_mecanica_cuantica/pwl-30-ene-2020/introduccion_a_mc.ipynb
index 044b42a..84a2ed5 100644
--- a/presentaciones/pwl_mecanica_cuantica/pwl-30-ene-2020/introduccion_a_mc.ipynb
+++ b/presentaciones/pwl_mecanica_cuantica/pwl-30-ene-2020/introduccion_a_mc.ipynb
@@ -1,1558 +1,1583 @@
-{
- "cells": [
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "source": [
- "# Advertencia"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 2,
- "metadata": {
- "slideshow": {
- "slide_type": "skip"
- }
- },
- "outputs": [],
- "source": [
- "import utils"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "source": [
- "# Parte I\n",
- "\n",
- "### El origen de la Mecánica Cuántica"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "source": [
- "## Episodio I : Old quantum mechanics"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 3,
- "metadata": {},
- "outputs": [
- {
- "data": {
- "text/html": [
- "\n",
- " <iframe\n",
- " width=\"600px\"\n",
- " height=\"400px\"\n",
- " src=\"https://phet.colorado.edu/sims/html/wave-interference/latest/wave-interference_en.html\"\n",
- " frameborder=\"0\"\n",
- " allowfullscreen\n",
- " ></iframe>\n",
- " "
- ],
- "text/plain": [
- "<IPython.lib.display.IFrame at 0x7f7c71f121c0>"
- ]
- },
- "execution_count": 3,
- "metadata": {},
- "output_type": "execute_result"
- }
- ],
- "source": [
- "utils.IFrame(src='https://phet.colorado.edu/sims/html/wave-interference/latest/wave-interference_en.html',\n",
- " width='600px',\n",
- " height='400px')"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "source": [
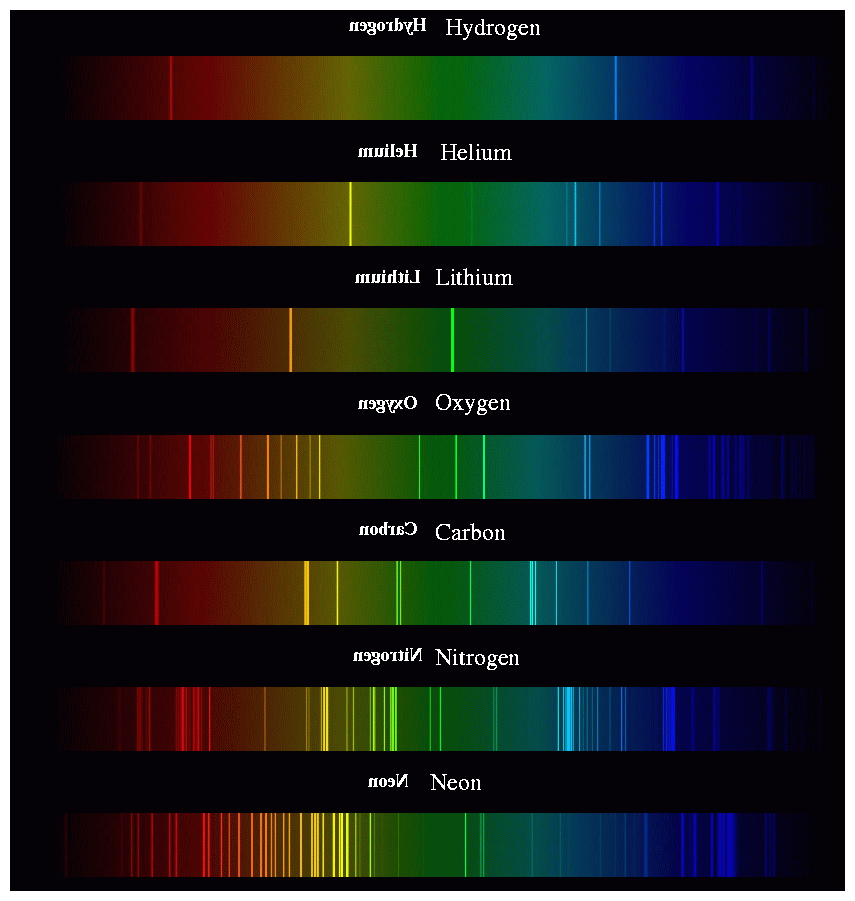
- "### Radiación del Cuerpo Negro y cuantización de la energía"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "source": [
- ""
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 2,
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "outputs": [
- {
- "data": {
- "text/html": [
- "<img src=\"https://cdn.britannica.com/47/8747-004-A1104E40/Wien.jpg\" width=\"200\" height=\"200\"/>"
- ],
- "text/plain": [
- "<utils.Photo object>"
- ]
- },
- "execution_count": 2,
- "metadata": {},
- "output_type": "execute_result"
- }
- ],
- "source": [
- "utils.Photo('Wien')"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "subslide"
- }
- },
- "source": [
- "$${\\displaystyle B_{\\nu }(T)\\approx {\\frac {2h\\nu ^{3}}{c^{2}}}e^{-{\\frac {h\\nu }{k_{\\mathrm {B} }T}}}}$$"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 3,
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "outputs": [
- {
- "data": {
- "text/html": [
- "<img src=\"https://cdn.britannica.com/s:300x1000/73/20973-050-F6EEBFF1/Max-Planck.jpg\" width=\"200\" height=\"200\"/>"
- ],
- "text/plain": [
- "<utils.Photo object>"
- ]
- },
- "execution_count": 3,
- "metadata": {},
- "output_type": "execute_result"
- }
- ],
- "source": [
- "utils.Photo('Plank')"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "subslide"
- }
- },
- "source": [
- ""
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "subslide"
- }
- },
- "source": [
- "$${\\displaystyle B_{\\nu }(\\nu ,T)={\\frac {2h\\nu ^{3}}{c^{2}}}{\\frac {1}{e^{\\frac {h\\nu }{k_{\\mathrm {B} }T}}-1}}}$$"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "subslide"
- }
- },
- "source": [
- "$${\\displaystyle B_{\\nu }(T)={\\frac {2\\nu ^{2}k_{\\mathrm {B} }T}{c^{2}}}}$$"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 4,
- "metadata": {},
- "outputs": [
- {
- "data": {
- "text/html": [
- "\n",
- " <iframe\n",
- " width=\"600px\"\n",
- " height=\"400px\"\n",
- " src=\"https://phet.colorado.edu/sims/html/blackbody-spectrum/latest/blackbody-spectrum_en.html\"\n",
- " frameborder=\"0\"\n",
- " allowfullscreen\n",
- " ></iframe>\n",
- " "
- ],
- "text/plain": [
- "<IPython.lib.display.IFrame at 0x7f7c71f127c0>"
- ]
- },
- "execution_count": 4,
- "metadata": {},
- "output_type": "execute_result"
- }
- ],
- "source": [
- "utils.IFrame(src='https://phet.colorado.edu/sims/html/blackbody-spectrum/latest/blackbody-spectrum_en.html',\n",
- " width='600px',\n",
- " height='400px')"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "source": [
- ""
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "fragment"
- }
- },
- "source": [
- "### Efecto Fotoeléctrico"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 4,
- "metadata": {
- "slideshow": {
- "slide_type": "fragment"
- }
- },
- "outputs": [
- {
- "data": {
- "text/html": [
- "<img src=\"https://cdn.britannica.com/09/75509-050-86D8CBBF/Albert-Einstein.jpg\" width=\"200\" height=\"200\"/>"
- ],
- "text/plain": [
- "<utils.Photo object>"
- ]
- },
- "execution_count": 4,
- "metadata": {},
- "output_type": "execute_result"
- }
- ],
- "source": [
- "utils.Photo('Einstein')"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "subslide"
- }
- },
- "source": [
- "\n",
- "\n",
- "[Simulación interactiva](https://phet.colorado.edu/en/simulation/legacy/photoelectric)"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "source": [
- ""
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 5,
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "outputs": [
- {
- "data": {
- "text/html": [
- "<img src=\"https://cdn.britannica.com/43/102243-050-15D49DEF/Ernest-Rutherford.jpg\" width=\"200\" height=\"200\"/>"
- ],
- "text/plain": [
- "<utils.Photo object>"
- ]
- },
- "execution_count": 5,
- "metadata": {},
- "output_type": "execute_result"
- }
- ],
- "source": [
- "utils.Photo('Rutherford')"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "metadata": {},
- "outputs": [],
- "source": [
- "utils.IFrame(src='https://phet.colorado.edu/sims/html/rutherford-scattering/latest/rutherford-scattering_en.html',\n",
- " width='600px',\n",
- " height='400px')"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "fragment"
- }
- },
- "source": [
- ""
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "source": [
- "### Espectro Atómico (Bohr, DeBroglie, Sommerfeld, Kramer)"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 6,
- "metadata": {
- "slideshow": {
- "slide_type": "subslide"
- }
- },
- "outputs": [
- {
- "data": {
- "text/html": [
- "<img src=\"https://cdn.britannica.com/s:300x1000/14/21114-004-FA0334F4/Niels-Bohr.jpg\" width=\"200\" height=\"200\"/>"
- ],
- "text/plain": [
- "<utils.Photo object>"
- ]
- },
- "execution_count": 6,
- "metadata": {},
- "output_type": "execute_result"
- }
- ],
- "source": [
- "utils.Photo('Bohr')"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 7,
- "metadata": {
- "slideshow": {
- "slide_type": "subslide"
- }
- },
- "outputs": [
- {
- "data": {
- "text/html": [
- "<img src=\"https://cdn.britannica.com/s:1500x700,q:85/09/21109-004-2172F5F5/Louis-Victor-Broglie-1958.jpg\" width=\"200\" height=\"200\"/>"
- ],
- "text/plain": [
- "<utils.Photo object>"
- ]
- },
- "execution_count": 7,
- "metadata": {},
- "output_type": "execute_result"
- }
- ],
- "source": [
- "utils.Photo('de Broglie')"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "fragment"
- }
- },
- "source": [
- "$$ E=n\\hbar \\omega \\, $$\n",
- "$$ \\int p\\,dx=\\hbar \\int k\\,dx=2\\pi \\hbar n $$"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 8,
- "metadata": {
- "slideshow": {
- "slide_type": "subslide"
- }
- },
- "outputs": [
- {
- "data": {
- "text/html": [
- "<img src=\"https://upload.wikimedia.org/wikipedia/commons/7/74/Sommerfeld1897.gif\" width=\"200\" height=\"200\"/>"
- ],
- "text/plain": [
- "<utils.Photo object>"
- ]
- },
- "execution_count": 8,
- "metadata": {},
- "output_type": "execute_result"
- }
- ],
- "source": [
- "utils.Photo('Sommerfeld')"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "fragment"
- }
- },
- "source": [
- "$$ \\oint \\limits _{H(p,q)=E}p_{i}\\,dq_{i}=n_{i}h $$"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 9,
- "metadata": {
- "slideshow": {
- "slide_type": "subslide"
- }
- },
- "outputs": [
- {
- "data": {
- "text/html": [
- "<img src=\"https://upload.wikimedia.org/wikipedia/commons/b/b4/Kramers_1928.jpg\" width=\"200\" height=\"200\"/>"
- ],
- "text/plain": [
- "<utils.Photo object>"
- ]
- },
- "execution_count": 9,
- "metadata": {},
- "output_type": "execute_result"
- }
- ],
- "source": [
- "utils.Photo('Kramers')"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "fragment"
- }
- },
- "source": [
- "$$ X_{n}(t)=\\sum _{k=-\\infty }^{\\infty }e^{ik\\omega t}X_{n;k} $$"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "source": [
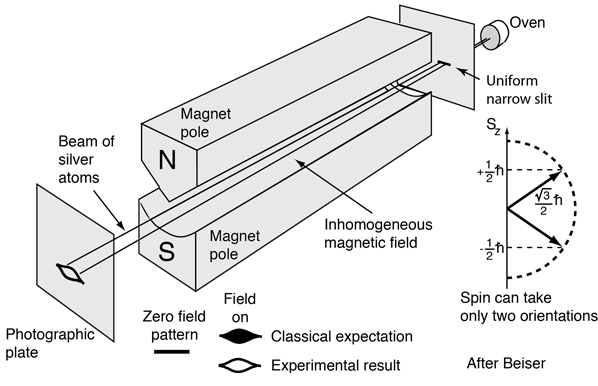
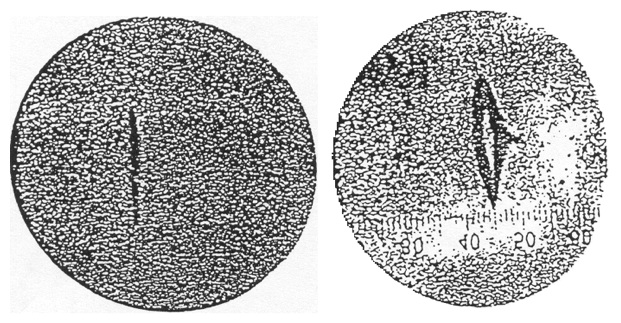
- "### Momento angular de los electrones / Spin (Stern-Gerlach)"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 10,
- "metadata": {
- "slideshow": {
- "slide_type": "subslide"
- }
- },
- "outputs": [
- {
- "data": {
- "text/html": [
- "<img src=\"https://cdn.britannica.com/06/134706-050-755B4B38/Otto-Stern-presentation-Nobel-Prizes-New-York-1943.jpg\" width=\"200\" height=\"200\"/>"
- ],
- "text/plain": [
- "<utils.Photo object>"
- ]
- },
- "execution_count": 10,
- "metadata": {},
- "output_type": "execute_result"
- }
- ],
- "source": [
- "utils.Photo('Stern')"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 11,
- "metadata": {
- "slideshow": {
- "slide_type": "subslide"
- }
- },
- "outputs": [
- {
- "data": {
- "text/html": [
- "<img src=\"https://upload.wikimedia.org/wikipedia/en/9/9e/Walther_Gerlach.jpg\" width=\"200\" height=\"200\"/>"
- ],
- "text/plain": [
- "<utils.Photo object>"
- ]
- },
- "execution_count": 11,
- "metadata": {},
- "output_type": "execute_result"
- }
- ],
- "source": [
- "utils.Photo('Gerlach')"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "subslide"
- }
- },
- "source": [
- ""
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "subslide"
- }
- },
- "source": [
- ""
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "fragment"
- }
- },
- "source": [
- "#### Simulación y comparación del modelo clásico y cuántico del momento mágnetico de un átomo\n",
- "https://nbviewer.jupyter.org/github/qutip/qutip-notebooks/blob/master/examples/stern-gerlach-tutorial.ipynb"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "source": [
- "## Episodio II\n",
- "\n",
- "### Modelos matemáticos de la MC"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 12,
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "outputs": [
- {
- "data": {
- "text/html": [
- "<img src=\"https://cdn.britannica.com/67/43167-004-A4FAD96F/Werner-Heisenberg.jpg\" width=\"200\" height=\"200\"/>"
- ],
- "text/plain": [
- "<utils.Photo object>"
- ]
- },
- "execution_count": 12,
- "metadata": {},
- "output_type": "execute_result"
- }
- ],
- "source": [
- "utils.Photo('Heisenberg')"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "subslide"
- }
- },
- "source": [
- "### Mecánica matricial de Heisenberg \n",
- " \n",
- "$$X_{{nm}}(t)=e^{{2\\pi i(E_{n}-E_{m})t/h}}X_{{nm}}(0)$$"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "fragment"
- }
- },
- "source": [
- "$$ {\\sqrt {2}}X(0)={\\sqrt {{\\frac {h}{2\\pi }}}}\\;{\\begin{bmatrix}0&{\\sqrt {1}}&0&0&0&\\cdots \\\\{\\sqrt {1}}&0&{\\sqrt {2}}&0&0&\\cdots \\\\0&{\\sqrt {2}}&0&{\\sqrt {3}}&0&\\cdots \\\\0&0&{\\sqrt {3}}&0&{\\sqrt {4}}&\\cdots \\\\\\vdots &\\vdots &\\vdots &\\vdots &\\vdots &\\ddots \\\\\\end{bmatrix}} $$"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 13,
- "metadata": {
- "slideshow": {
- "slide_type": "subslide"
- }
- },
- "outputs": [
- {
- "data": {
- "text/html": [
- "<img src=\"https://cdn.britannica.com/24/13124-004-E329BF69/Max-Born.jpg\" width=\"200\" height=\"200\"/>"
- ],
- "text/plain": [
- "<utils.Photo object>"
- ]
- },
- "execution_count": 13,
- "metadata": {},
- "output_type": "execute_result"
- }
- ],
- "source": [
- "utils.Photo('Born')"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 14,
- "metadata": {
- "slideshow": {
- "slide_type": "subslide"
- }
- },
- "outputs": [
- {
- "data": {
- "text/html": [
- "<img src=\"https://upload.wikimedia.org/wikipedia/commons/a/a6/Pascual_Jordan_1920s.jpg\" width=\"200\" height=\"200\"/>"
- ],
- "text/plain": [
- "<utils.Photo object>"
- ]
- },
- "execution_count": 14,
- "metadata": {},
- "output_type": "execute_result"
- }
- ],
- "source": [
- "utils.Photo('Jordan')"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "source": [
- "$$ (XP)_{{mn}}=\\sum _{{k=0}}^{\\infty }X_{{mk}}P_{{kn}} $$"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "subslide"
- }
- },
- "source": [
- "$$ \\sum _{k}(X_{{nk}}P_{{km}}-P_{{nk}}X_{{km}})={ih \\over 2\\pi }~\\delta _{{nm}} $$"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "source": [
- "$$ \\frac{dA}{dt} = {i \\over \\hbar } [ H , A ] + \\frac{\\partial A}{\\partial t} $$"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 5,
- "metadata": {
- "slideshow": {
- "slide_type": "subslide"
- }
- },
- "outputs": [
- {
- "data": {
- "text/html": [
- "<img src=\"https://cdn.britannica.com/16/198816-050-AF8B7B3C/Erwin-Schrodinger.jpg\" width=\"200\" height=\"200\"/>"
- ],
- "text/plain": [
- "<utils.Photo object>"
- ]
- },
- "execution_count": 5,
- "metadata": {},
- "output_type": "execute_result"
- }
- ],
- "source": [
- "utils.Photo('Schrodinger')"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "subslide"
- }
- },
- "source": [
- "### Mecánica ondulatoria de Schrodinger"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "fragment"
- }
- },
- "source": [
- "$$i{\\partial \\over \\partial t}\\psi _{t}(x)=\\left[-{1 \\over 2m}{\\partial ^{2} \\over \\partial x^{2}}+V(x)\\right]\\psi _{t}(x)$$"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "metadata": {
- "slideshow": {
- "slide_type": "fragment"
- }
- },
- "outputs": [],
- "source": []
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "source": [
- "### Formalización y notación de Bra-Ket"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 16,
- "metadata": {
- "slideshow": {
- "slide_type": "subslide"
- }
- },
- "outputs": [
- {
- "data": {
- "text/html": [
- "<img src=\"https://cdn.britannica.com/66/91766-004-CE5A2E61/PAM-Dirac.jpg\" width=\"200\" height=\"200\"/>"
- ],
- "text/plain": [
- "<utils.Photo object>"
- ]
- },
- "execution_count": 16,
- "metadata": {},
- "output_type": "execute_result"
- }
- ],
- "source": [
- "utils.Photo('Dirac')"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 17,
- "metadata": {
- "slideshow": {
- "slide_type": "subslide"
- }
- },
- "outputs": [
- {
- "data": {
- "text/html": [
- "<img src=\"https://cdn.britannica.com/23/26823-050-E778F3DF/John-von-Neumann.jpg\" width=\"200\" height=\"200\"/>"
- ],
- "text/plain": [
- "<utils.Photo object>"
- ]
- },
- "execution_count": 17,
- "metadata": {},
- "output_type": "execute_result"
- }
- ],
- "source": [
- "utils.Photo('von Neumann')"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "source": [
- "$$ |\\psi\\rangle $$\n",
- "\n",
- "$${\\displaystyle \\Psi (\\mathbf {r} )\\ {\\stackrel {\\text{def}}{=}}\\ \\langle \\mathbf {r} |\\Psi \\rangle }$$"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "source": [
- ""
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "source": [
- "# Parte II"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "fragment"
- }
- },
- "source": [
- "## Introducción a la matemática de la MC"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "source": [
- " A Hilbert space H is a real or complex inner product space that is also a complete metric space with respect to the distance function induced by the inner product"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "source": [
- ""
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "source": [
- "### A little Aaronson time"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "subslide"
- }
- },
- "source": [
- "# QM = Prob + \"-\""
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "fragment"
- }
- },
- "source": [
- "# Probabilidad\n",
- "\n",
- "Sea un conjunto de eventos posibles $\\Omega$\n",
- "\n",
- "$$f(x)\\in [0,1]{\\mbox{ para todo }}x\\in \\Omega$$\n",
- "$$\\sum _{x\\in \\Omega }f(x)=1 $$"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 18,
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "outputs": [],
- "source": [
- "from sympy import Matrix, init_printing\n",
- "init_printing(use_latex=True)"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 32,
- "metadata": {},
- "outputs": [
- {
- "data": {
- "text/latex": [
- "$\\displaystyle \\left[\\begin{matrix}0.5 & 0.5\\\\0.5 & 0.5\\end{matrix}\\right]$"
- ],
- "text/plain": [
- "⎡0.5 0.5⎤\n",
- "⎢ ⎥\n",
- "⎣0.5 0.5⎦"
- ]
- },
- "execution_count": 32,
- "metadata": {},
- "output_type": "execute_result"
- }
- ],
- "source": [
- "Ma"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 19,
- "metadata": {
- "slideshow": {
- "slide_type": "fragment"
- }
- },
- "outputs": [
- {
- "data": {
- "text/latex": [
- "$\\displaystyle \\left( \\left[\\begin{matrix}0.5\\\\0.5\\end{matrix}\\right], \\ \\left[\\begin{matrix}0.333333333333333\\\\0.666666666666667\\end{matrix}\\right], \\ \\left[\\begin{matrix}0.99\\\\0.01\\end{matrix}\\right]\\right)$"
- ],
- "text/plain": [
- "⎛⎡0.5⎤ ⎡0.333333333333333⎤ ⎡0.99⎤⎞\n",
- "⎜⎢ ⎥, ⎢ ⎥, ⎢ ⎥⎟\n",
- "⎝⎣0.5⎦ ⎣0.666666666666667⎦ ⎣0.01⎦⎠"
- ]
- },
- "execution_count": 19,
- "metadata": {},
- "output_type": "execute_result"
- }
- ],
- "source": [
- "Ma, Mb, Mc = Matrix([[1/2,1/2],[1/2,1/2]]), Matrix([[1/3,1/5],[2/3,4/5]]), Matrix([[99/100,0],[1/100,1]])\n",
- "s = Matrix([[1],[0]])\n",
- "Ma*s, Mb*s, Mc*s"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "metadata": {},
- "outputs": [],
- "source": []
- },
- {
- "cell_type": "code",
- "execution_count": 20,
- "metadata": {
- "slideshow": {
- "slide_type": "fragment"
- }
- },
- "outputs": [
- {
- "data": {
- "text/latex": [
- "$\\displaystyle \\left[\\begin{matrix}0.230769230769232\\\\0.769230769230774\\end{matrix}\\right]$"
- ],
- "text/plain": [
- "⎡0.230769230769232⎤\n",
- "⎢ ⎥\n",
- "⎣0.769230769230774⎦"
- ]
- },
- "execution_count": 20,
- "metadata": {},
- "output_type": "execute_result"
- }
- ],
- "source": [
- "Mb**200 * s"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "source": [
- "# ¿Qué obtendríamos si en vez de la Norma 1 imponemos la condición de normalización con la Norma 2?"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "fragment"
- }
- },
- "source": [
- "$$f(x)\\in \\mathbb {C} {\\mbox{ para todo }}x\\in \\Omega$$\n",
- "$$\\sum _{x\\in \\Omega }\\overline {f(x)}* f(x) =1 $$"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 21,
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "outputs": [],
- "source": [
- "from sympy import sqrt, symbols, Symbol, init_printing\n",
- "from sympy.physics.quantum import Bra, Ket, Dagger, Operator"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "source": [
- "## Postulados de la MC"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "source": [
- "## Postulado 1\n",
- "\n",
- "El estado de todo sistema físico está representado por un vector (de norma unidad) en un espacio de Hilbert $\\mathcal{H}$ "
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 22,
- "metadata": {
- "slideshow": {
- "slide_type": "subslide"
- }
- },
- "outputs": [
- {
- "data": {
- "text/latex": [
- "$\\displaystyle \\alpha {\\left|\\psi\\right\\rangle } + \\beta {\\left|\\phi\\right\\rangle }$"
- ],
- "text/plain": [
- "α⋅❘ψ⟩ + β⋅❘φ⟩"
- ]
- },
- "execution_count": 22,
- "metadata": {},
- "output_type": "execute_result"
- }
- ],
- "source": [
- "a, b = symbols('alpha beta',complex=True)\n",
- "psi, phi = Ket('psi'),Ket('phi')\n",
- "\n",
- "estado = a * psi + b * phi\n",
- "estado"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 23,
- "metadata": {
- "slideshow": {
- "slide_type": "fragment"
- }
- },
- "outputs": [
- {
- "data": {
- "text/latex": [
- "$\\displaystyle \\overline{\\alpha} {\\left\\langle \\psi\\right|} + \\overline{\\beta} {\\left\\langle \\phi\\right|}$"
- ],
- "text/plain": [
- "_ _ \n",
- "α⋅⟨ψ❘ + β⋅⟨φ❘"
- ]
- },
- "execution_count": 23,
- "metadata": {},
- "output_type": "execute_result"
- }
- ],
- "source": [
- "Dagger(estado)"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 24,
- "metadata": {
- "slideshow": {
- "slide_type": "fragment"
- }
- },
- "outputs": [
- {
- "data": {
- "text/latex": [
- "$\\displaystyle \\left(\\overline{\\alpha} {\\left\\langle \\psi\\right|} + \\overline{\\beta} {\\left\\langle \\phi\\right|}\\right) \\left(\\alpha {\\left|\\psi\\right\\rangle } + \\beta {\\left|\\phi\\right\\rangle }\\right)$"
- ],
- "text/plain": [
- "⎛_ _ ⎞ \n",
- "⎝α⋅⟨ψ❘ + β⋅⟨φ❘⎠⋅(α⋅❘ψ⟩ + β⋅❘φ⟩)"
- ]
- },
- "execution_count": 24,
- "metadata": {},
- "output_type": "execute_result"
- }
- ],
- "source": [
- "( Dagger(estado) * estado ).doit()"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "source": [
- "## Postulado 2\n",
- "\n",
- "Todas las propiedades observables de un sistema físico se prepresentan por un operador lineal hermítico que actúa sobre $\\mathcal{H}$"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "metadata": {},
- "outputs": [],
- "source": []
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "source": [
- "## Postulado 3\n",
- "\n",
- "Los resultados posibles de la medición de cualquier observable $A$ son sus autovalores $a_n$"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "metadata": {
- "slideshow": {
- "slide_type": "fragment"
- }
- },
- "outputs": [],
- "source": []
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "source": [
- "## Postulado 4 ( Regla de Born )\n",
- "\n",
- "\n",
- "\n",
- "Si el estado de un sistema es $\\left|\\Psi\\right\\rangle$, la probabilidad de obtener el resultado $a_n$ en la medición del observable $A$ es siempre\n",
- "\n",
- "$$ Prob\\left(a_n | \\left|\\Psi\\right\\rangle \\right) = \\left\\langle \\Psi\\right| P_n \\left|\\Psi\\right\\rangle $$\n",
- "\n",
- "donde $P_n$ es el proyector asociado al autovalor $a_n$. Si $A$ es no degenerado entonce $P_n = {\\left|\\phi_{n}\\right\\rangle }{\\left\\langle \\phi_{n}\\right|}$ y la probabilidad resulta ser $$Prob\\left( a_n | \\left|\\Psi\\right\\rangle \\right) = \\left| \\left\\langle \\phi_{n} |\\Psi\\right\\rangle \\right|^2$$"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "metadata": {
- "slideshow": {
- "slide_type": "fragment"
- }
- },
- "outputs": [],
- "source": []
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "source": [
- "## Postulado 5 ( Postulado de proyección o colapso )\n",
- "\n",
- "Si el estado de un sistema es ${\\left|\\Psi\\right\\rangle }$ y medimos el observable $A$ y detectamos el autovalor $a_n$, entonces el estado del sistema después \n",
- "de la medición es la proyección de ${\\left|\\Psi\\right\\rangle }$ sobre el subespacio asociado al autovalor $a_n$\n"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "outputs": [],
- "source": []
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "metadata": {
- "slideshow": {
- "slide_type": "subslide"
- }
- },
- "outputs": [],
- "source": []
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "metadata": {
- "slideshow": {
- "slide_type": "subslide"
- }
- },
- "outputs": [],
- "source": []
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "metadata": {
- "slideshow": {
- "slide_type": "subslide"
- }
- },
- "outputs": [],
- "source": []
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "source": [
- "# Parte III\n",
- "\n",
- "## Sistemas compuestos"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 25,
- "metadata": {
- "slideshow": {
- "slide_type": "subslide"
- }
- },
- "outputs": [],
- "source": [
- "from sympy.physics.quantum import TensorProduct"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 26,
- "metadata": {
- "slideshow": {
- "slide_type": "subslide"
- }
- },
- "outputs": [],
- "source": [
- "j,k,l = Ket('j'), Ket('k'), Ket('l')\n",
- "A, B = Operator('A'), Operator('B')"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 27,
- "metadata": {
- "slideshow": {
- "slide_type": "subslide"
- }
- },
- "outputs": [
- {
- "data": {
- "text/latex": [
- "$\\displaystyle {{\\left|j\\right\\rangle }}\\otimes {{\\left|k\\right\\rangle }}$"
- ],
- "text/plain": [
- "❘j⟩⨂ ❘k⟩"
- ]
- },
- "execution_count": 27,
- "metadata": {},
- "output_type": "execute_result"
- }
- ],
- "source": [
- "jk = TensorProduct(j,k)\n",
- "jk"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "source": [
- "## Partículas idénticas "
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "source": [
- "## Paradoja de EPR\n",
- "\n",
- "$$|\\Phi ^{+}\\rangle ={\\frac {1}{{\\sqrt {2}}}}(|0\\rangle _{A}\\otimes |0\\rangle _{B}+|1\\rangle _{A}\\otimes |1\\rangle _{B})$$"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 28,
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "outputs": [],
- "source": [
- "from sympy.physics.quantum.qubit import Qubit"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 29,
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "outputs": [
- {
- "data": {
- "text/latex": [
- "$\\displaystyle \\frac{\\sqrt{2} \\left({\\left|00\\right\\rangle } + {\\left|11\\right\\rangle }\\right)}{2}$"
- ],
- "text/plain": [
- "√2⋅(❘00⟩ + ❘11⟩)\n",
- "────────────────\n",
- " 2 "
- ]
- },
- "execution_count": 29,
- "metadata": {},
- "output_type": "execute_result"
- }
- ],
- "source": [
- "( Qubit('00') + Qubit('11') )/sqrt(2)"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "source": [
- "## Desigualdad de Bell"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "subslide"
- }
- },
- "source": [
- "Ejemplo de [Teleportación](https://hub.gke.mybinder.org/user/sympy-quantum_notebooks-alf8r713/notebooks/notebooks/teleportation.ipynb)"
- ]
- }
- ],
- "metadata": {
- "celltoolbar": "Slideshow",
- "kernelspec": {
- "display_name": "Python 3",
- "language": "python",
- "name": "python3"
- },
- "language_info": {
- "codemirror_mode": {
- "name": "ipython",
- "version": 3
- },
- "file_extension": ".py",
- "mimetype": "text/x-python",
- "name": "python",
- "nbconvert_exporter": "python",
- "pygments_lexer": "ipython3",
- "version": "3.8.0"
- }
- },
- "nbformat": 4,
- "nbformat_minor": 4
-}
+{
+ "cells": [
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "slideshow": {
+ "slide_type": "slide"
+ }
+ },
+ "source": [
+ "# Advertencia"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 1,
+ "metadata": {
+ "slideshow": {
+ "slide_type": "skip"
+ }
+ },
+ "outputs": [],
+ "source": [
+ "import utils"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "slideshow": {
+ "slide_type": "slide"
+ }
+ },
+ "source": [
+ "# Parte I\n",
+ "\n",
+ "### El origen de la Mecánica Cuántica"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "slideshow": {
+ "slide_type": "slide"
+ }
+ },
+ "source": [
+ "## Episodio I : Old quantum mechanics"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 2,
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "text/html": [
+ "\n",
+ " <iframe\n",
+ " width=\"600px\"\n",
+ " height=\"400px\"\n",
+ " src=\"https://phet.colorado.edu/sims/html/wave-interference/latest/wave-interference_en.html\"\n",
+ " frameborder=\"0\"\n",
+ " allowfullscreen\n",
+ " \n",
+ " ></iframe>\n",
+ " "
+ ],
+ "text/plain": [
+ "<IPython.lib.display.IFrame at 0x1d13d356630>"
+ ]
+ },
+ "execution_count": 2,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "utils.IFrame(src='https://phet.colorado.edu/sims/html/wave-interference/latest/wave-interference_en.html',\n",
+ " width='600px',\n",
+ " height='400px')"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "slideshow": {
+ "slide_type": "slide"
+ }
+ },
+ "source": [
+ "### Radiación del Cuerpo Negro y cuantización de la energía"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "slideshow": {
+ "slide_type": "slide"
+ }
+ },
+ "source": [
+ ""
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 3,
+ "metadata": {
+ "slideshow": {
+ "slide_type": "slide"
+ }
+ },
+ "outputs": [
+ {
+ "data": {
+ "text/html": [
+ "<img src=\"https://cdn.britannica.com/47/8747-004-A1104E40/Wien.jpg\" width=\"200\" height=\"200\"/>"
+ ],
+ "text/plain": [
+ "<utils.Photo object>"
+ ]
+ },
+ "execution_count": 3,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "utils.Photo('Wien')"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "slideshow": {
+ "slide_type": "subslide"
+ }
+ },
+ "source": [
+ "$${\\displaystyle B_{\\nu }(T)\\approx {\\frac {2h\\nu ^{3}}{c^{2}}}e^{-{\\frac {h\\nu }{k_{\\mathrm {B} }T}}}}$$"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 4,
+ "metadata": {
+ "slideshow": {
+ "slide_type": "slide"
+ }
+ },
+ "outputs": [
+ {
+ "data": {
+ "text/html": [
+ "<img src=\"https://cdn.britannica.com/s:300x1000/73/20973-050-F6EEBFF1/Max-Planck.jpg\" width=\"200\" height=\"200\"/>"
+ ],
+ "text/plain": [
+ "<utils.Photo object>"
+ ]
+ },
+ "execution_count": 4,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "utils.Photo('Plank')"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "slideshow": {
+ "slide_type": "subslide"
+ }
+ },
+ "source": [
+ ""
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "slideshow": {
+ "slide_type": "subslide"
+ }
+ },
+ "source": [
+ "$${\\displaystyle B_{\\nu }(\\nu ,T)={\\frac {2h\\nu ^{3}}{c^{2}}}{\\frac {1}{e^{\\frac {h\\nu }{k_{\\mathrm {B} }T}}-1}}}$$"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "slideshow": {
+ "slide_type": "subslide"
+ }
+ },
+ "source": [
+ "$${\\displaystyle B_{\\nu }(T)={\\frac {2\\nu ^{2}k_{\\mathrm {B} }T}{c^{2}}}}$$"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 5,
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "text/html": [
+ "\n",
+ " <iframe\n",
+ " width=\"600px\"\n",
+ " height=\"400px\"\n",
+ " src=\"https://phet.colorado.edu/sims/html/blackbody-spectrum/latest/blackbody-spectrum_en.html\"\n",
+ " frameborder=\"0\"\n",
+ " allowfullscreen\n",
+ " \n",
+ " ></iframe>\n",
+ " "
+ ],
+ "text/plain": [
+ "<IPython.lib.display.IFrame at 0x1d13e901520>"
+ ]
+ },
+ "execution_count": 5,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "utils.IFrame(src='https://phet.colorado.edu/sims/html/blackbody-spectrum/latest/blackbody-spectrum_en.html',\n",
+ " width='600px',\n",
+ " height='400px')"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "slideshow": {
+ "slide_type": "slide"
+ }
+ },
+ "source": [
+ ""
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "slideshow": {
+ "slide_type": "fragment"
+ }
+ },
+ "source": [
+ "### Efecto Fotoeléctrico"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 6,
+ "metadata": {
+ "slideshow": {
+ "slide_type": "fragment"
+ }
+ },
+ "outputs": [
+ {
+ "data": {
+ "text/html": [
+ "<img src=\"https://cdn.britannica.com/09/75509-050-86D8CBBF/Albert-Einstein.jpg\" width=\"200\" height=\"200\"/>"
+ ],
+ "text/plain": [
+ "<utils.Photo object>"
+ ]
+ },
+ "execution_count": 6,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "utils.Photo('Einstein')"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "slideshow": {
+ "slide_type": "subslide"
+ }
+ },
+ "source": [
+ "\n",
+ "\n",
+ "[Simulación interactiva](https://phet.colorado.edu/en/simulation/legacy/photoelectric)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "slideshow": {
+ "slide_type": "slide"
+ }
+ },
+ "source": [
+ ""
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 7,
+ "metadata": {
+ "slideshow": {
+ "slide_type": "slide"
+ }
+ },
+ "outputs": [
+ {
+ "data": {
+ "text/html": [
+ "<img src=\"https://cdn.britannica.com/43/102243-050-15D49DEF/Ernest-Rutherford.jpg\" width=\"200\" height=\"200\"/>"
+ ],
+ "text/plain": [
+ "<utils.Photo object>"
+ ]
+ },
+ "execution_count": 7,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "utils.Photo('Rutherford')"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 8,
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "text/html": [
+ "\n",
+ " <iframe\n",
+ " width=\"600px\"\n",
+ " height=\"400px\"\n",
+ " src=\"https://phet.colorado.edu/sims/html/rutherford-scattering/latest/rutherford-scattering_en.html\"\n",
+ " frameborder=\"0\"\n",
+ " allowfullscreen\n",
+ " \n",
+ " ></iframe>\n",
+ " "
+ ],
+ "text/plain": [
+ "<IPython.lib.display.IFrame at 0x1d13e9218e0>"
+ ]
+ },
+ "execution_count": 8,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "utils.IFrame(src='https://phet.colorado.edu/sims/html/rutherford-scattering/latest/rutherford-scattering_en.html',\n",
+ " width='600px',\n",
+ " height='400px')"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "slideshow": {
+ "slide_type": "fragment"
+ }
+ },
+ "source": [
+ ""
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "slideshow": {
+ "slide_type": "slide"
+ }
+ },
+ "source": [
+ "### Espectro Atómico (Bohr, DeBroglie, Sommerfeld, Kramer)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 9,
+ "metadata": {
+ "slideshow": {
+ "slide_type": "subslide"
+ }
+ },
+ "outputs": [
+ {
+ "data": {
+ "text/html": [
+ "<img src=\"https://cdn.britannica.com/s:300x1000/14/21114-004-FA0334F4/Niels-Bohr.jpg\" width=\"200\" height=\"200\"/>"
+ ],
+ "text/plain": [
+ "<utils.Photo object>"
+ ]
+ },
+ "execution_count": 9,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "utils.Photo('Bohr')"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 10,
+ "metadata": {
+ "slideshow": {
+ "slide_type": "subslide"
+ }
+ },
+ "outputs": [
+ {
+ "data": {
+ "text/html": [
+ "<img src=\"https://cdn.britannica.com/s:1500x700,q:85/09/21109-004-2172F5F5/Louis-Victor-Broglie-1958.jpg\" width=\"200\" height=\"200\"/>"
+ ],
+ "text/plain": [
+ "<utils.Photo object>"
+ ]
+ },
+ "execution_count": 10,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "utils.Photo('de Broglie')"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "slideshow": {
+ "slide_type": "fragment"
+ }
+ },
+ "source": [
+ "$$ E=n\\hbar \\omega \\, $$\n",
+ "$$ \\int p\\,dx=\\hbar \\int k\\,dx=2\\pi \\hbar n $$"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 11,
+ "metadata": {
+ "slideshow": {
+ "slide_type": "subslide"
+ }
+ },
+ "outputs": [
+ {
+ "data": {
+ "text/html": [
+ "<img src=\"https://upload.wikimedia.org/wikipedia/commons/7/74/Sommerfeld1897.gif\" width=\"200\" height=\"200\"/>"
+ ],
+ "text/plain": [
+ "<utils.Photo object>"
+ ]
+ },
+ "execution_count": 11,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "utils.Photo('Sommerfeld')"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "slideshow": {
+ "slide_type": "fragment"
+ }
+ },
+ "source": [
+ "$$ \\oint \\limits _{H(p,q)=E}p_{i}\\,dq_{i}=n_{i}h $$"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 12,
+ "metadata": {
+ "slideshow": {
+ "slide_type": "subslide"
+ }
+ },
+ "outputs": [
+ {
+ "data": {
+ "text/html": [
+ "<img src=\"https://upload.wikimedia.org/wikipedia/commons/b/b4/Kramers_1928.jpg\" width=\"200\" height=\"200\"/>"
+ ],
+ "text/plain": [
+ "<utils.Photo object>"
+ ]
+ },
+ "execution_count": 12,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "utils.Photo('Kramers')"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "slideshow": {
+ "slide_type": "fragment"
+ }
+ },
+ "source": [
+ "$$ X_{n}(t)=\\sum _{k=-\\infty }^{\\infty }e^{ik\\omega t}X_{n;k} $$"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "slideshow": {
+ "slide_type": "slide"
+ }
+ },
+ "source": [
+ "### Momento angular de los electrones / Spin (Stern-Gerlach)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 13,
+ "metadata": {
+ "slideshow": {
+ "slide_type": "subslide"
+ }
+ },
+ "outputs": [
+ {
+ "data": {
+ "text/html": [
+ "<img src=\"https://cdn.britannica.com/06/134706-050-755B4B38/Otto-Stern-presentation-Nobel-Prizes-New-York-1943.jpg\" width=\"200\" height=\"200\"/>"
+ ],
+ "text/plain": [
+ "<utils.Photo object>"
+ ]
+ },
+ "execution_count": 13,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "utils.Photo('Stern')"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 14,
+ "metadata": {
+ "slideshow": {
+ "slide_type": "subslide"
+ }
+ },
+ "outputs": [
+ {
+ "data": {
+ "text/html": [
+ "<img src=\"https://upload.wikimedia.org/wikipedia/en/9/9e/Walther_Gerlach.jpg\" width=\"200\" height=\"200\"/>"
+ ],
+ "text/plain": [
+ "<utils.Photo object>"
+ ]
+ },
+ "execution_count": 14,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "utils.Photo('Gerlach')"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "slideshow": {
+ "slide_type": "subslide"
+ }
+ },
+ "source": [
+ ""
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "slideshow": {
+ "slide_type": "subslide"
+ }
+ },
+ "source": [
+ ""
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "slideshow": {
+ "slide_type": "fragment"
+ }
+ },
+ "source": [
+ "#### Simulación y comparación del modelo clásico y cuántico del momento mágnetico de un átomo\n",
+ "https://nbviewer.jupyter.org/github/qutip/qutip-notebooks/blob/master/examples/stern-gerlach-tutorial.ipynb"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "slideshow": {
+ "slide_type": "slide"
+ }
+ },
+ "source": [
+ "## Episodio II\n",
+ "\n",
+ "### Modelos matemáticos de la MC"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 15,
+ "metadata": {
+ "slideshow": {
+ "slide_type": "slide"
+ }
+ },
+ "outputs": [
+ {
+ "data": {
+ "text/html": [
+ "<img src=\"https://cdn.britannica.com/67/43167-004-A4FAD96F/Werner-Heisenberg.jpg\" width=\"200\" height=\"200\"/>"
+ ],
+ "text/plain": [
+ "<utils.Photo object>"
+ ]
+ },
+ "execution_count": 15,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "utils.Photo('Heisenberg')"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "slideshow": {
+ "slide_type": "subslide"
+ }
+ },
+ "source": [
+ "### Mecánica matricial de Heisenberg \n",
+ " \n",
+ "$$X_{{nm}}(t)=e^{{2\\pi i(E_{n}-E_{m})t/h}}X_{{nm}}(0)$$"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "slideshow": {
+ "slide_type": "fragment"
+ }
+ },
+ "source": [
+ "$$ {\\sqrt {2}}X(0)={\\sqrt {{\\frac {h}{2\\pi }}}}\\;{\\begin{bmatrix}0&{\\sqrt {1}}&0&0&0&\\cdots \\\\{\\sqrt {1}}&0&{\\sqrt {2}}&0&0&\\cdots \\\\0&{\\sqrt {2}}&0&{\\sqrt {3}}&0&\\cdots \\\\0&0&{\\sqrt {3}}&0&{\\sqrt {4}}&\\cdots \\\\\\vdots &\\vdots &\\vdots &\\vdots &\\vdots &\\ddots \\\\\\end{bmatrix}} $$"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 16,
+ "metadata": {
+ "slideshow": {
+ "slide_type": "subslide"
+ }
+ },
+ "outputs": [
+ {
+ "data": {
+ "text/html": [
+ "<img src=\"https://cdn.britannica.com/24/13124-004-E329BF69/Max-Born.jpg\" width=\"200\" height=\"200\"/>"
+ ],
+ "text/plain": [
+ "<utils.Photo object>"
+ ]
+ },
+ "execution_count": 16,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "utils.Photo('Born')"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 17,
+ "metadata": {
+ "slideshow": {
+ "slide_type": "subslide"
+ }
+ },
+ "outputs": [
+ {
+ "data": {
+ "text/html": [
+ "<img src=\"https://upload.wikimedia.org/wikipedia/commons/a/a6/Pascual_Jordan_1920s.jpg\" width=\"200\" height=\"200\"/>"
+ ],
+ "text/plain": [
+ "<utils.Photo object>"
+ ]
+ },
+ "execution_count": 17,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "utils.Photo('Jordan')"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "slideshow": {
+ "slide_type": "slide"
+ }
+ },
+ "source": [
+ "$$ (XP)_{{mn}}=\\sum _{{k=0}}^{\\infty }X_{{mk}}P_{{kn}} $$"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "slideshow": {
+ "slide_type": "subslide"
+ }
+ },
+ "source": [
+ "$$ \\sum _{k}(X_{{nk}}P_{{km}}-P_{{nk}}X_{{km}})={ih \\over 2\\pi }~\\delta _{{nm}} $$"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "slideshow": {
+ "slide_type": "slide"
+ }
+ },
+ "source": [
+ "$$ \\frac{dA}{dt} = {i \\over \\hbar } [ H , A ] + \\frac{\\partial A}{\\partial t} $$"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 18,
+ "metadata": {
+ "slideshow": {
+ "slide_type": "subslide"
+ }
+ },
+ "outputs": [
+ {
+ "data": {
+ "text/html": [
+ "<img src=\"https://cdn.britannica.com/16/198816-050-AF8B7B3C/Erwin-Schrodinger.jpg\" width=\"200\" height=\"200\"/>"
+ ],
+ "text/plain": [
+ "<utils.Photo object>"
+ ]
+ },
+ "execution_count": 18,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "utils.Photo('Schrodinger')"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "slideshow": {
+ "slide_type": "subslide"
+ }
+ },
+ "source": [
+ "### Mecánica ondulatoria de Schrodinger"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "slideshow": {
+ "slide_type": "fragment"
+ }
+ },
+ "source": [
+ "$$i{\\partial \\over \\partial t}\\psi _{t}(x)=\\left[-{1 \\over 2m}{\\partial ^{2} \\over \\partial x^{2}}+V(x)\\right]\\psi _{t}(x)$$"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "slideshow": {
+ "slide_type": "fragment"
+ }
+ },
+ "outputs": [],
+ "source": []
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "slideshow": {
+ "slide_type": "slide"
+ }
+ },
+ "source": [
+ "### Formalización y notación de Bra-Ket"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 19,
+ "metadata": {
+ "slideshow": {
+ "slide_type": "subslide"
+ }
+ },
+ "outputs": [
+ {
+ "data": {
+ "text/html": [
+ "<img src=\"https://cdn.britannica.com/66/91766-004-CE5A2E61/PAM-Dirac.jpg\" width=\"200\" height=\"200\"/>"
+ ],
+ "text/plain": [
+ "<utils.Photo object>"
+ ]
+ },
+ "execution_count": 19,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "utils.Photo('Dirac')"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 20,
+ "metadata": {
+ "slideshow": {
+ "slide_type": "subslide"
+ }
+ },
+ "outputs": [
+ {
+ "data": {
+ "text/html": [
+ "<img src=\"https://cdn.britannica.com/23/26823-050-E778F3DF/John-von-Neumann.jpg\" width=\"200\" height=\"200\"/>"
+ ],
+ "text/plain": [
+ "<utils.Photo object>"
+ ]
+ },
+ "execution_count": 20,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "utils.Photo('von Neumann')"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "slideshow": {
+ "slide_type": "slide"
+ }
+ },
+ "source": [
+ "$$ |\\psi\\rangle $$\n",
+ "\n",
+ "$${\\displaystyle \\Psi (\\mathbf {r} )\\ {\\stackrel {\\text{def}}{=}}\\ \\langle \\mathbf {r} |\\Psi \\rangle }$$"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "slideshow": {
+ "slide_type": "slide"
+ }
+ },
+ "source": [
+ ""
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "slideshow": {
+ "slide_type": "slide"
+ }
+ },
+ "source": [
+ "# Parte II"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "slideshow": {
+ "slide_type": "fragment"
+ }
+ },
+ "source": [
+ "## Introducción a la matemática de la MC"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "slideshow": {
+ "slide_type": "slide"
+ }
+ },
+ "source": [
+ " A Hilbert space H is a real or complex inner product space that is also a complete metric space with respect to the distance function induced by the inner product"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "slideshow": {
+ "slide_type": "slide"
+ }
+ },
+ "source": [
+ ""
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "slideshow": {
+ "slide_type": "slide"
+ }
+ },
+ "source": [
+ "### A little Aaronson time"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "slideshow": {
+ "slide_type": "subslide"
+ }
+ },
+ "source": [
+ "# QM = Prob + \"-\""
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "slideshow": {
+ "slide_type": "fragment"
+ }
+ },
+ "source": [
+ "# Probabilidad\n",
+ "\n",
+ "Sea un conjunto de eventos posibles $\\Omega$\n",
+ "\n",
+ "$$f(x)\\in [0,1]{\\mbox{ para todo }}x\\in \\Omega$$\n",
+ "$$\\sum _{x\\in \\Omega }f(x)=1 $$"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 21,
+ "metadata": {
+ "slideshow": {
+ "slide_type": "slide"
+ }
+ },
+ "outputs": [],
+ "source": [
+ "from sympy import Matrix, init_printing\n",
+ "init_printing(use_latex=True)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 22,
+ "metadata": {
+ "slideshow": {
+ "slide_type": "fragment"
+ }
+ },
+ "outputs": [
+ {
+ "data": {
+ "text/latex": [
+ "$\\displaystyle \\left( \\left[\\begin{matrix}0.5\\\\0.5\\end{matrix}\\right], \\ \\left[\\begin{matrix}0.333333333333333\\\\0.666666666666667\\end{matrix}\\right], \\ \\left[\\begin{matrix}0.99\\\\0.01\\end{matrix}\\right]\\right)$"
+ ],
+ "text/plain": [
+ "⎛⎡0.5⎤ ⎡0.333333333333333⎤ ⎡0.99⎤⎞\n",
+ "⎜⎢ ⎥, ⎢ ⎥, ⎢ ⎥⎟\n",
+ "⎝⎣0.5⎦ ⎣0.666666666666667⎦ ⎣0.01⎦⎠"
+ ]
+ },
+ "execution_count": 22,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "Ma, Mb, Mc = Matrix([[1/2,1/2],[1/2,1/2]]), Matrix([[1/3,1/5],[2/3,4/5]]), Matrix([[99/100,0],[1/100,1]])\n",
+ "s = Matrix([[1],[0]])\n",
+ "Ma*s, Mb*s, Mc*s"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 23,
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "text/latex": [
+ "$\\displaystyle \\left[\\begin{matrix}0.5 & 0.5\\\\0.5 & 0.5\\end{matrix}\\right]$"
+ ],
+ "text/plain": [
+ "⎡0.5 0.5⎤\n",
+ "⎢ ⎥\n",
+ "⎣0.5 0.5⎦"
+ ]
+ },
+ "execution_count": 23,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "Ma"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {},
+ "outputs": [],
+ "source": []
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 24,
+ "metadata": {
+ "slideshow": {
+ "slide_type": "fragment"
+ }
+ },
+ "outputs": [
+ {
+ "data": {
+ "text/latex": [
+ "$\\displaystyle \\left[\\begin{matrix}0.230769230769232\\\\0.769230769230774\\end{matrix}\\right]$"
+ ],
+ "text/plain": [
+ "⎡0.230769230769232⎤\n",
+ "⎢ ⎥\n",
+ "⎣0.769230769230774⎦"
+ ]
+ },
+ "execution_count": 24,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "Mb**200 * s"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "slideshow": {
+ "slide_type": "slide"
+ }
+ },
+ "source": [
+ "# ¿Qué obtendríamos si en vez de la Norma 1 imponemos la condición de normalización con la Norma 2?"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "slideshow": {
+ "slide_type": "fragment"
+ }
+ },
+ "source": [
+ "$$f(x)\\in \\mathbb {C} {\\mbox{ para todo }}x\\in \\Omega$$\n",
+ "$$\\sum _{x\\in \\Omega }\\overline {f(x)}* f(x) =1 $$"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 25,
+ "metadata": {
+ "slideshow": {
+ "slide_type": "slide"
+ }
+ },
+ "outputs": [],
+ "source": [
+ "from sympy import sqrt, symbols, Symbol, init_printing\n",
+ "from sympy.physics.quantum import Bra, Ket, Dagger, Operator"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "slideshow": {
+ "slide_type": "slide"
+ }
+ },
+ "source": [
+ "## Postulados de la MC"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "slideshow": {
+ "slide_type": "slide"
+ }
+ },
+ "source": [
+ "## Postulado 1\n",
+ "\n",
+ "El estado de todo sistema físico está representado por un vector (de norma unidad) en un espacio de Hilbert $\\mathcal{H}$ "
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 26,
+ "metadata": {
+ "slideshow": {
+ "slide_type": "subslide"
+ }
+ },
+ "outputs": [
+ {
+ "data": {
+ "text/latex": [
+ "$\\displaystyle \\alpha {\\left|\\psi\\right\\rangle } + \\beta {\\left|\\phi\\right\\rangle }$"
+ ],
+ "text/plain": [
+ "α⋅❘ψ⟩ + β⋅❘φ⟩"
+ ]
+ },
+ "execution_count": 26,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "a, b = symbols('alpha beta',complex=True)\n",
+ "psi, phi = Ket('psi'),Ket('phi')\n",
+ "\n",
+ "estado = a * psi + b * phi\n",
+ "estado"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 27,
+ "metadata": {
+ "slideshow": {
+ "slide_type": "fragment"
+ }
+ },
+ "outputs": [
+ {
+ "data": {
+ "text/latex": [
+ "$\\displaystyle \\overline{\\alpha} {\\left\\langle \\psi\\right|} + \\overline{\\beta} {\\left\\langle \\phi\\right|}$"
+ ],
+ "text/plain": [
+ "_ _ \n",
+ "α⋅⟨ψ❘ + β⋅⟨φ❘"
+ ]
+ },
+ "execution_count": 27,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "Dagger(estado)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 28,
+ "metadata": {
+ "slideshow": {
+ "slide_type": "fragment"
+ }
+ },
+ "outputs": [
+ {
+ "data": {
+ "text/latex": [
+ "$\\displaystyle \\left(\\overline{\\alpha} {\\left\\langle \\psi\\right|} + \\overline{\\beta} {\\left\\langle \\phi\\right|}\\right) \\left(\\alpha {\\left|\\psi\\right\\rangle } + \\beta {\\left|\\phi\\right\\rangle }\\right)$"
+ ],
+ "text/plain": [
+ "⎛_ _ ⎞ \n",
+ "⎝α⋅⟨ψ❘ + β⋅⟨φ❘⎠⋅(α⋅❘ψ⟩ + β⋅❘φ⟩)"
+ ]
+ },
+ "execution_count": 28,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "( Dagger(estado) * estado ).doit()"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "slideshow": {
+ "slide_type": "slide"
+ }
+ },
+ "source": [
+ "## Postulado 2\n",
+ "\n",
+ "Todas las propiedades observables de un sistema físico se prepresentan por un operador lineal hermítico que actúa sobre $\\mathcal{H}$"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {},
+ "outputs": [],
+ "source": []
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "slideshow": {
+ "slide_type": "slide"
+ }
+ },
+ "source": [
+ "## Postulado 3\n",
+ "\n",
+ "Los resultados posibles de la medición de cualquier observable $A$ son sus autovalores $a_n$"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "slideshow": {
+ "slide_type": "fragment"
+ }
+ },
+ "outputs": [],
+ "source": []
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "slideshow": {
+ "slide_type": "slide"
+ }
+ },
+ "source": [
+ "## Postulado 4 ( Regla de Born )\n",
+ "\n",
+ "\n",
+ "\n",
+ "Si el estado de un sistema es $\\left|\\Psi\\right\\rangle$, la probabilidad de obtener el resultado $a_n$ en la medición del observable $A$ es siempre\n",
+ "\n",
+ "$$ Prob\\left(a_n | \\left|\\Psi\\right\\rangle \\right) = \\left\\langle \\Psi\\right| P_n \\left|\\Psi\\right\\rangle $$\n",
+ "\n",
+ "donde $P_n$ es el proyector asociado al autovalor $a_n$. Si $A$ es no degenerado entonce $P_n = {\\left|\\phi_{n}\\right\\rangle }{\\left\\langle \\phi_{n}\\right|}$ y la probabilidad resulta ser $$Prob\\left( a_n | \\left|\\Psi\\right\\rangle \\right) = \\left| \\left\\langle \\phi_{n} |\\Psi\\right\\rangle \\right|^2$$"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "slideshow": {
+ "slide_type": "fragment"
+ }
+ },
+ "outputs": [],
+ "source": []
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "slideshow": {
+ "slide_type": "slide"
+ }
+ },
+ "source": [
+ "## Postulado 5 ( Postulado de proyección o colapso )\n",
+ "\n",
+ "Si el estado de un sistema es ${\\left|\\Psi\\right\\rangle }$ y medimos el observable $A$ y detectamos el autovalor $a_n$, entonces el estado del sistema después \n",
+ "de la medición es la proyección de ${\\left|\\Psi\\right\\rangle }$ sobre el subespacio asociado al autovalor $a_n$\n"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "slideshow": {
+ "slide_type": "slide"
+ }
+ },
+ "outputs": [],
+ "source": []
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "slideshow": {
+ "slide_type": "subslide"
+ }
+ },
+ "outputs": [],
+ "source": []
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "slideshow": {
+ "slide_type": "subslide"
+ }
+ },
+ "outputs": [],
+ "source": []
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "slideshow": {
+ "slide_type": "subslide"
+ }
+ },
+ "outputs": [],
+ "source": []
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "slideshow": {
+ "slide_type": "slide"
+ }
+ },
+ "source": [
+ "# Parte III\n",
+ "\n",
+ "## Sistemas compuestos"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 29,
+ "metadata": {
+ "slideshow": {
+ "slide_type": "subslide"
+ }
+ },
+ "outputs": [],
+ "source": [
+ "from sympy.physics.quantum import TensorProduct"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 30,
+ "metadata": {
+ "slideshow": {
+ "slide_type": "subslide"
+ }
+ },
+ "outputs": [],
+ "source": [
+ "j,k,l = Ket('j'), Ket('k'), Ket('l')\n",
+ "A, B = Operator('A'), Operator('B')"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 31,
+ "metadata": {
+ "slideshow": {
+ "slide_type": "subslide"
+ }
+ },
+ "outputs": [
+ {
+ "data": {
+ "text/latex": [
+ "$\\displaystyle {{\\left|j\\right\\rangle }}\\otimes {{\\left|k\\right\\rangle }}$"
+ ],
+ "text/plain": [
+ "❘j⟩⨂ ❘k⟩"
+ ]
+ },
+ "execution_count": 31,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "jk = TensorProduct(j,k)\n",
+ "jk"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "slideshow": {
+ "slide_type": "slide"
+ }
+ },
+ "source": [
+ "## Partículas idénticas "
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "slideshow": {
+ "slide_type": "slide"
+ }
+ },
+ "source": [
+ "## Paradoja de EPR\n",
+ "\n",
+ "$$|\\Phi ^{+}\\rangle ={\\frac {1}{{\\sqrt {2}}}}(|0\\rangle _{A}\\otimes |0\\rangle _{B}+|1\\rangle _{A}\\otimes |1\\rangle _{B})$$"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 32,
+ "metadata": {
+ "slideshow": {
+ "slide_type": "slide"
+ }
+ },
+ "outputs": [],
+ "source": [
+ "from sympy.physics.quantum.qubit import Qubit"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 33,
+ "metadata": {
+ "slideshow": {
+ "slide_type": "slide"
+ }
+ },
+ "outputs": [
+ {
+ "data": {
+ "text/latex": [
+ "$\\displaystyle \\frac{\\sqrt{2} \\left({\\left|00\\right\\rangle } + {\\left|11\\right\\rangle }\\right)}{2}$"
+ ],
+ "text/plain": [
+ "√2⋅(❘00⟩ + ❘11⟩)\n",
+ "────────────────\n",
+ " 2 "
+ ]
+ },
+ "execution_count": 33,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "( Qubit('00') + Qubit('11') )/sqrt(2)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "slideshow": {
+ "slide_type": "slide"
+ }
+ },
+ "source": [
+ "## Desigualdad de Bell"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "slideshow": {
+ "slide_type": "subslide"
+ }
+ },
+ "source": [
+ "Ejemplo de [Teleportación](https://hub.gke.mybinder.org/user/sympy-quantum_notebooks-alf8r713/notebooks/notebooks/teleportation.ipynb)"
+ ]
+ }
+ ],
+ "metadata": {
+ "celltoolbar": "Slideshow",
+ "kernelspec": {
+ "display_name": "Python 3 (ipykernel)",
+ "language": "python",
+ "name": "python3"
+ },
+ "language_info": {
+ "codemirror_mode": {
+ "name": "ipython",
+ "version": 3
+ },
+ "file_extension": ".py",
+ "mimetype": "text/x-python",
+ "name": "python",
+ "nbconvert_exporter": "python",
+ "pygments_lexer": "ipython3",
+ "version": "3.12.1"
+ }
+ },
+ "nbformat": 4,
+ "nbformat_minor": 4
+}
diff --git a/presentaciones/pyar_hypotesis/pyar-28-ago-2019/presentation.ipynb b/presentaciones/pyar_hypotesis/pyar-28-ago-2019/presentation.ipynb
index aac3a36..b1eb0d9 100644
--- a/presentaciones/pyar_hypotesis/pyar-28-ago-2019/presentation.ipynb
+++ b/presentaciones/pyar_hypotesis/pyar-28-ago-2019/presentation.ipynb
@@ -2,7 +2,7 @@
"cells": [
{
"cell_type": "code",
- "execution_count": 3,
+ "execution_count": 1,
"metadata": {
"scrolled": true,
"slideshow": {
@@ -898,7 +898,7 @@
"metadata": {
"celltoolbar": "Slideshow",
"kernelspec": {
- "display_name": "Python 3",
+ "display_name": "Python 3 (ipykernel)",
"language": "python",
"name": "python3"
},
@@ -912,9 +912,9 @@
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
- "version": "3.7.4"
+ "version": "3.12.1"
}
},
"nbformat": 4,
- "nbformat_minor": 2
+ "nbformat_minor": 4
}
diff --git a/presentaciones/pyconar_2019/widgets-presentation.ipynb b/presentaciones/pyconar_2019/widgets-presentation.ipynb
index 420c5c3..b6b3ae7 100644
--- a/presentaciones/pyconar_2019/widgets-presentation.ipynb
+++ b/presentaciones/pyconar_2019/widgets-presentation.ipynb
@@ -213,7 +213,7 @@
"name": "stdout",
"output_type": "stream",
"text": [
- "<__main__.Cosito object at 0x7fc2b159ff10>\n"
+ "<__main__.Cosito object at 0x000002664553B920>\n"
]
}
],
@@ -240,13 +240,22 @@
},
{
"cell_type": "code",
- "execution_count": null,
+ "execution_count": 2,
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
- "outputs": [],
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "Esto es str: ruflete\n",
+ "Esto es repr: Cosito(\"ruflete\")\n"
+ ]
+ }
+ ],
"source": [
"class Cosito:\n",
" \n",
@@ -288,7 +297,7 @@
},
{
"cell_type": "code",
- "execution_count": 2,
+ "execution_count": 3,
"metadata": {
"slideshow": {
"slide_type": "subslide"
@@ -312,7 +321,7 @@
"Cosito(\"ruflete\")"
]
},
- "execution_count": 2,
+ "execution_count": 3,
"metadata": {},
"output_type": "execute_result"
}
@@ -342,7 +351,7 @@
},
{
"cell_type": "code",
- "execution_count": 3,
+ "execution_count": 4,
"metadata": {
"slideshow": {
"slide_type": "subslide"
@@ -356,7 +365,7 @@
},
{
"cell_type": "code",
- "execution_count": 4,
+ "execution_count": 5,
"metadata": {
"slideshow": {
"slide_type": "fragment"
@@ -389,7 +398,7 @@
},
{
"cell_type": "code",
- "execution_count": 5,
+ "execution_count": 6,
"metadata": {
"slideshow": {
"slide_type": "subslide"
@@ -407,7 +416,7 @@
{
"data": {
"application/vnd.jupyter.widget-view+json": {
- "model_id": "cb8fa4f9b73a48c4a7ad5ea185543b69",
+ "model_id": "f55c4846eb8a48e796ae486afd3af851",
"version_major": 2,
"version_minor": 0
},
@@ -439,7 +448,7 @@
},
{
"cell_type": "code",
- "execution_count": 6,
+ "execution_count": 7,
"metadata": {
"slideshow": {
"slide_type": "subslide"
@@ -452,8 +461,9 @@
"Cosito()"
]
},
+ "execution_count": 7,
"metadata": {},
- "output_type": "display_data"
+ "output_type": "execute_result"
}
],
"source": [
@@ -515,13 +525,21 @@
},
{
"cell_type": "code",
- "execution_count": null,
+ "execution_count": 8,
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
- "outputs": [],
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "Ring ring!\n"
+ ]
+ }
+ ],
"source": [
"def llamado(cambio):\n",
" print('Ring ring!')\n",
@@ -577,7 +595,7 @@
},
{
"cell_type": "code",
- "execution_count": null,
+ "execution_count": 9,
"metadata": {
"slideshow": {
"slide_type": "subslide"
@@ -628,13 +646,39 @@
},
{
"cell_type": "code",
- "execution_count": null,
+ "execution_count": 10,
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
- "outputs": [],
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "Ring ring!\n"
+ ]
+ },
+ {
+ "ename": "ValueError",
+ "evalue": "No deberías hacer eso",
+ "output_type": "error",
+ "traceback": [
+ "\u001b[1;31m---------------------------------------------------------------------------\u001b[0m",
+ "\u001b[1;31mValueError\u001b[0m Traceback (most recent call last)",
+ "Cell \u001b[1;32mIn[10], line 5\u001b[0m\n\u001b[0;32m 2\u001b[0m \u001b[38;5;28;01mraise\u001b[39;00m \u001b[38;5;167;01mValueError\u001b[39;00m(\u001b[38;5;124m'\u001b[39m\u001b[38;5;124mNo deberías hacer eso\u001b[39m\u001b[38;5;124m'\u001b[39m)\n\u001b[0;32m 4\u001b[0m ruflete\u001b[38;5;241m.\u001b[39mobserve(intentar_encastrar)\n\u001b[1;32m----> 5\u001b[0m \u001b[43mruflete\u001b[49m\u001b[38;5;241;43m.\u001b[39;49m\u001b[43mtamanio\u001b[49m \u001b[38;5;241m=\u001b[39m \u001b[38;5;241m0\u001b[39m\n\u001b[0;32m 6\u001b[0m ruflete\n",
+ "File \u001b[1;32m~\\dev\\gh\\akielbowicz\\presentations\\.venv\\Lib\\site-packages\\traitlets\\traitlets.py:716\u001b[0m, in \u001b[0;36mTraitType.__set__\u001b[1;34m(self, obj, value)\u001b[0m\n\u001b[0;32m 714\u001b[0m \u001b[38;5;28;01mif\u001b[39;00m \u001b[38;5;28mself\u001b[39m\u001b[38;5;241m.\u001b[39mread_only:\n\u001b[0;32m 715\u001b[0m \u001b[38;5;28;01mraise\u001b[39;00m TraitError(\u001b[38;5;124m'\u001b[39m\u001b[38;5;124mThe \u001b[39m\u001b[38;5;124m\"\u001b[39m\u001b[38;5;132;01m%s\u001b[39;00m\u001b[38;5;124m\"\u001b[39m\u001b[38;5;124m trait is read-only.\u001b[39m\u001b[38;5;124m'\u001b[39m \u001b[38;5;241m%\u001b[39m \u001b[38;5;28mself\u001b[39m\u001b[38;5;241m.\u001b[39mname)\n\u001b[1;32m--> 716\u001b[0m \u001b[38;5;28;43mself\u001b[39;49m\u001b[38;5;241;43m.\u001b[39;49m\u001b[43mset\u001b[49m\u001b[43m(\u001b[49m\u001b[43mobj\u001b[49m\u001b[43m,\u001b[49m\u001b[43m \u001b[49m\u001b[43mvalue\u001b[49m\u001b[43m)\u001b[49m\n",
+ "File \u001b[1;32m~\\dev\\gh\\akielbowicz\\presentations\\.venv\\Lib\\site-packages\\traitlets\\traitlets.py:706\u001b[0m, in \u001b[0;36mTraitType.set\u001b[1;34m(self, obj, value)\u001b[0m\n\u001b[0;32m 702\u001b[0m silent \u001b[38;5;241m=\u001b[39m \u001b[38;5;28;01mFalse\u001b[39;00m\n\u001b[0;32m 703\u001b[0m \u001b[38;5;28;01mif\u001b[39;00m silent \u001b[38;5;129;01mis\u001b[39;00m \u001b[38;5;129;01mnot\u001b[39;00m \u001b[38;5;28;01mTrue\u001b[39;00m:\n\u001b[0;32m 704\u001b[0m \u001b[38;5;66;03m# we explicitly compare silent to True just in case the equality\u001b[39;00m\n\u001b[0;32m 705\u001b[0m \u001b[38;5;66;03m# comparison above returns something other than True/False\u001b[39;00m\n\u001b[1;32m--> 706\u001b[0m \u001b[43mobj\u001b[49m\u001b[38;5;241;43m.\u001b[39;49m\u001b[43m_notify_trait\u001b[49m\u001b[43m(\u001b[49m\u001b[38;5;28;43mself\u001b[39;49m\u001b[38;5;241;43m.\u001b[39;49m\u001b[43mname\u001b[49m\u001b[43m,\u001b[49m\u001b[43m \u001b[49m\u001b[43mold_value\u001b[49m\u001b[43m,\u001b[49m\u001b[43m \u001b[49m\u001b[43mnew_value\u001b[49m\u001b[43m)\u001b[49m\n",
+ "File \u001b[1;32m~\\dev\\gh\\akielbowicz\\presentations\\.venv\\Lib\\site-packages\\traitlets\\traitlets.py:1513\u001b[0m, in \u001b[0;36mHasTraits._notify_trait\u001b[1;34m(self, name, old_value, new_value)\u001b[0m\n\u001b[0;32m 1512\u001b[0m \u001b[38;5;28;01mdef\u001b[39;00m \u001b[38;5;21m_notify_trait\u001b[39m(\u001b[38;5;28mself\u001b[39m, name: \u001b[38;5;28mstr\u001b[39m, old_value: t\u001b[38;5;241m.\u001b[39mAny, new_value: t\u001b[38;5;241m.\u001b[39mAny) \u001b[38;5;241m-\u001b[39m\u001b[38;5;241m>\u001b[39m \u001b[38;5;28;01mNone\u001b[39;00m:\n\u001b[1;32m-> 1513\u001b[0m \u001b[38;5;28;43mself\u001b[39;49m\u001b[38;5;241;43m.\u001b[39;49m\u001b[43mnotify_change\u001b[49m\u001b[43m(\u001b[49m\n\u001b[0;32m 1514\u001b[0m \u001b[43m \u001b[49m\u001b[43mBunch\u001b[49m\u001b[43m(\u001b[49m\n\u001b[0;32m 1515\u001b[0m \u001b[43m \u001b[49m\u001b[43mname\u001b[49m\u001b[38;5;241;43m=\u001b[39;49m\u001b[43mname\u001b[49m\u001b[43m,\u001b[49m\n\u001b[0;32m 1516\u001b[0m \u001b[43m \u001b[49m\u001b[43mold\u001b[49m\u001b[38;5;241;43m=\u001b[39;49m\u001b[43mold_value\u001b[49m\u001b[43m,\u001b[49m\n\u001b[0;32m 1517\u001b[0m \u001b[43m \u001b[49m\u001b[43mnew\u001b[49m\u001b[38;5;241;43m=\u001b[39;49m\u001b[43mnew_value\u001b[49m\u001b[43m,\u001b[49m\n\u001b[0;32m 1518\u001b[0m \u001b[43m \u001b[49m\u001b[43mowner\u001b[49m\u001b[38;5;241;43m=\u001b[39;49m\u001b[38;5;28;43mself\u001b[39;49m\u001b[43m,\u001b[49m\n\u001b[0;32m 1519\u001b[0m \u001b[43m \u001b[49m\u001b[38;5;28;43mtype\u001b[39;49m\u001b[38;5;241;43m=\u001b[39;49m\u001b[38;5;124;43m\"\u001b[39;49m\u001b[38;5;124;43mchange\u001b[39;49m\u001b[38;5;124;43m\"\u001b[39;49m\u001b[43m,\u001b[49m\n\u001b[0;32m 1520\u001b[0m \u001b[43m \u001b[49m\u001b[43m)\u001b[49m\n\u001b[0;32m 1521\u001b[0m \u001b[43m \u001b[49m\u001b[43m)\u001b[49m\n",
+ "File \u001b[1;32m~\\dev\\gh\\akielbowicz\\presentations\\.venv\\Lib\\site-packages\\ipywidgets\\widgets\\widget.py:701\u001b[0m, in \u001b[0;36mWidget.notify_change\u001b[1;34m(self, change)\u001b[0m\n\u001b[0;32m 698\u001b[0m \u001b[38;5;28;01mif\u001b[39;00m name \u001b[38;5;129;01min\u001b[39;00m \u001b[38;5;28mself\u001b[39m\u001b[38;5;241m.\u001b[39mkeys \u001b[38;5;129;01mand\u001b[39;00m \u001b[38;5;28mself\u001b[39m\u001b[38;5;241m.\u001b[39m_should_send_property(name, \u001b[38;5;28mgetattr\u001b[39m(\u001b[38;5;28mself\u001b[39m, name)):\n\u001b[0;32m 699\u001b[0m \u001b[38;5;66;03m# Send new state to front-end\u001b[39;00m\n\u001b[0;32m 700\u001b[0m \u001b[38;5;28mself\u001b[39m\u001b[38;5;241m.\u001b[39msend_state(key\u001b[38;5;241m=\u001b[39mname)\n\u001b[1;32m--> 701\u001b[0m \u001b[38;5;28;43msuper\u001b[39;49m\u001b[43m(\u001b[49m\u001b[43m)\u001b[49m\u001b[38;5;241;43m.\u001b[39;49m\u001b[43mnotify_change\u001b[49m\u001b[43m(\u001b[49m\u001b[43mchange\u001b[49m\u001b[43m)\u001b[49m\n",
+ "File \u001b[1;32m~\\dev\\gh\\akielbowicz\\presentations\\.venv\\Lib\\site-packages\\traitlets\\traitlets.py:1525\u001b[0m, in \u001b[0;36mHasTraits.notify_change\u001b[1;34m(self, change)\u001b[0m\n\u001b[0;32m 1523\u001b[0m \u001b[38;5;28;01mdef\u001b[39;00m \u001b[38;5;21mnotify_change\u001b[39m(\u001b[38;5;28mself\u001b[39m, change: Bunch) \u001b[38;5;241m-\u001b[39m\u001b[38;5;241m>\u001b[39m \u001b[38;5;28;01mNone\u001b[39;00m:\n\u001b[0;32m 1524\u001b[0m \u001b[38;5;250m \u001b[39m\u001b[38;5;124;03m\"\"\"Notify observers of a change event\"\"\"\u001b[39;00m\n\u001b[1;32m-> 1525\u001b[0m \u001b[38;5;28;01mreturn\u001b[39;00m \u001b[38;5;28;43mself\u001b[39;49m\u001b[38;5;241;43m.\u001b[39;49m\u001b[43m_notify_observers\u001b[49m\u001b[43m(\u001b[49m\u001b[43mchange\u001b[49m\u001b[43m)\u001b[49m\n",
+ "File \u001b[1;32m~\\dev\\gh\\akielbowicz\\presentations\\.venv\\Lib\\site-packages\\traitlets\\traitlets.py:1568\u001b[0m, in \u001b[0;36mHasTraits._notify_observers\u001b[1;34m(self, event)\u001b[0m\n\u001b[0;32m 1565\u001b[0m \u001b[38;5;28;01melif\u001b[39;00m \u001b[38;5;28misinstance\u001b[39m(c, EventHandler) \u001b[38;5;129;01mand\u001b[39;00m c\u001b[38;5;241m.\u001b[39mname \u001b[38;5;129;01mis\u001b[39;00m \u001b[38;5;129;01mnot\u001b[39;00m \u001b[38;5;28;01mNone\u001b[39;00m:\n\u001b[0;32m 1566\u001b[0m c \u001b[38;5;241m=\u001b[39m \u001b[38;5;28mgetattr\u001b[39m(\u001b[38;5;28mself\u001b[39m, c\u001b[38;5;241m.\u001b[39mname)\n\u001b[1;32m-> 1568\u001b[0m \u001b[43mc\u001b[49m\u001b[43m(\u001b[49m\u001b[43mevent\u001b[49m\u001b[43m)\u001b[49m\n",
+ "Cell \u001b[1;32mIn[10], line 2\u001b[0m, in \u001b[0;36mintentar_encastrar\u001b[1;34m(cambio)\u001b[0m\n\u001b[0;32m 1\u001b[0m \u001b[38;5;28;01mdef\u001b[39;00m \u001b[38;5;21mintentar_encastrar\u001b[39m(cambio):\n\u001b[1;32m----> 2\u001b[0m \u001b[38;5;28;01mraise\u001b[39;00m \u001b[38;5;167;01mValueError\u001b[39;00m(\u001b[38;5;124m'\u001b[39m\u001b[38;5;124mNo deberías hacer eso\u001b[39m\u001b[38;5;124m'\u001b[39m)\n",
+ "\u001b[1;31mValueError\u001b[0m: No deberías hacer eso"
+ ]
+ }
+ ],
"source": [
"def intentar_encastrar(cambio):\n",
" raise ValueError('No deberías hacer eso')\n",
@@ -646,13 +690,29 @@
},
{
"cell_type": "code",
- "execution_count": null,
+ "execution_count": 11,
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
- "outputs": [],
+ "outputs": [
+ {
+ "data": {
+ "application/vnd.jupyter.widget-view+json": {
+ "model_id": "2cebb87554b74f9a9052a86daf43f2ce",
+ "version_major": 2,
+ "version_minor": 0
+ },
+ "text/plain": [
+ "Output(layout=Layout(border_bottom='1px solid black', border_left='1px solid black', border_right='1px solid b…"
+ ]
+ },
+ "execution_count": 11,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
"source": [
"from ipywidgets import Output\n",
"output = Output(layout={'border': '1px solid black'})\n",
@@ -689,7 +749,7 @@
},
{
"cell_type": "code",
- "execution_count": null,
+ "execution_count": 12,
"metadata": {
"slideshow": {
"slide_type": "subslide"
@@ -824,17 +884,17 @@
]
},
{
- "cell_type": "code",
- "execution_count": null,
+ "cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
- "outputs": [],
"source": [
- "class Reloj(DomWidget):\n",
- " value = Date(None, allow_none=True).tag(sync=True, **date_serialization)"
+ "```python\n",
+ "class Reloj(DOMWidget):\n",
+ " value = Date(None, allow_none=True).tag(sync=True, **date_serialization)\n",
+ "```"
]
},
{
@@ -907,7 +967,7 @@
},
{
"cell_type": "code",
- "execution_count": null,
+ "execution_count": 13,
"metadata": {
"slideshow": {
"slide_type": "fragment"
@@ -968,7 +1028,7 @@
},
{
"cell_type": "code",
- "execution_count": null,
+ "execution_count": 14,
"metadata": {
"slideshow": {
"slide_type": "subslide"
@@ -998,7 +1058,7 @@
},
{
"cell_type": "code",
- "execution_count": null,
+ "execution_count": 15,
"metadata": {
"slideshow": {
"slide_type": "subslide"
@@ -1098,7 +1158,7 @@
"metadata": {
"celltoolbar": "Slideshow",
"kernelspec": {
- "display_name": "Python 3",
+ "display_name": "Python 3 (ipykernel)",
"language": "python",
"name": "python3"
},
@@ -1112,7 +1172,7 @@
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
- "version": "3.8.0"
+ "version": "3.12.1"
}
},
"nbformat": 4,
diff --git a/presentaciones/pyconar_2020/diapositivas.ipynb b/presentaciones/pyconar_2020/diapositivas.ipynb
index e78488e..7a09b47 100644
--- a/presentaciones/pyconar_2020/diapositivas.ipynb
+++ b/presentaciones/pyconar_2020/diapositivas.ipynb
@@ -361,7 +361,7 @@
},
{
"cell_type": "code",
- "execution_count": 4,
+ "execution_count": 3,
"metadata": {
"slideshow": {
"slide_type": "subslide"
@@ -383,7 +383,7 @@
"'22'"
]
},
- "execution_count": 4,
+ "execution_count": 3,
"metadata": {},
"output_type": "execute_result"
}
@@ -411,7 +411,7 @@
},
{
"cell_type": "code",
- "execution_count": 5,
+ "execution_count": 4,
"metadata": {
"slideshow": {
"slide_type": "subslide"
@@ -428,7 +428,7 @@
},
{
"cell_type": "code",
- "execution_count": 6,
+ "execution_count": 5,
"metadata": {
"slideshow": {
"slide_type": "subslide"
@@ -444,7 +444,7 @@
},
{
"cell_type": "code",
- "execution_count": 7,
+ "execution_count": 6,
"metadata": {
"slideshow": {
"slide_type": "fragment"
@@ -466,7 +466,7 @@
"'Este llamado fue interceptado con otra_funcion_usual(2)'"
]
},
- "execution_count": 7,
+ "execution_count": 6,
"metadata": {},
"output_type": "execute_result"
}
@@ -477,7 +477,7 @@
},
{
"cell_type": "code",
- "execution_count": 8,
+ "execution_count": 7,
"metadata": {
"slideshow": {
"slide_type": "subslide"
@@ -493,7 +493,7 @@
},
{
"cell_type": "code",
- "execution_count": 9,
+ "execution_count": 8,
"metadata": {
"slideshow": {
"slide_type": "fragment"
@@ -515,7 +515,7 @@
"'Este llamado fue interceptado con otra_funcion_usual(2)'"
]
},
- "execution_count": 9,
+ "execution_count": 8,
"metadata": {},
"output_type": "execute_result"
}
@@ -550,7 +550,7 @@
},
{
"cell_type": "code",
- "execution_count": 10,
+ "execution_count": 9,
"metadata": {
"slideshow": {
"slide_type": "subslide"
@@ -559,12 +559,13 @@
"outputs": [],
"source": [
"def imprimir_y_nada_mas(objeto_a_decorar):\n",
- " print(objeto_a_decorar)"
+ " print(objeto_a_decorar)\n",
+ " return objeto_a_decorar"
]
},
{
"cell_type": "code",
- "execution_count": 11,
+ "execution_count": 10,
"metadata": {
"slideshow": {
"slide_type": "subslide"
@@ -575,7 +576,7 @@
"name": "stdout",
"output_type": "stream",
"text": [
- "<function funcion_que_transforma_su_argumento at 0x7f1b7813db80>\n"
+ "<function funcion_que_transforma_su_argumento at 0x00000175664C3600>\n"
]
}
],
@@ -587,7 +588,7 @@
},
{
"cell_type": "code",
- "execution_count": 13,
+ "execution_count": 11,
"metadata": {
"slideshow": {
"slide_type": "subslide"
@@ -595,19 +596,18 @@
},
"outputs": [
{
- "ename": "TypeError",
- "evalue": "'NoneType' object is not callable",
- "output_type": "error",
- "traceback": [
- "\u001b[0;31m---------------------------------------------------------------------------\u001b[0m",
- "\u001b[0;31mTypeError\u001b[0m Traceback (most recent call last)",
- "\u001b[0;32m<ipython-input-13-448d641bdd6e>\u001b[0m in \u001b[0;36m<module>\u001b[0;34m\u001b[0m\n\u001b[0;32m----> 1\u001b[0;31m \u001b[0mfuncion_que_transforma_su_argumento\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;36m1\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m",
- "\u001b[0;31mTypeError\u001b[0m: 'NoneType' object is not callable"
- ]
+ "data": {
+ "text/plain": [
+ "'2222222222'"
+ ]
+ },
+ "execution_count": 11,
+ "metadata": {},
+ "output_type": "execute_result"
}
],
"source": [
- "funcion_que_transforma_su_argumento(1)"
+ "funcion_que_transforma_su_argumento(2)"
]
},
{
@@ -624,7 +624,7 @@
},
{
"cell_type": "code",
- "execution_count": 14,
+ "execution_count": 12,
"metadata": {
"slideshow": {
"slide_type": "subslide"
@@ -646,7 +646,7 @@
},
{
"cell_type": "code",
- "execution_count": 15,
+ "execution_count": 13,
"metadata": {
"slideshow": {
"slide_type": "subslide"
@@ -661,7 +661,7 @@
},
{
"cell_type": "code",
- "execution_count": 16,
+ "execution_count": 14,
"metadata": {
"slideshow": {
"slide_type": "subslide"
@@ -674,7 +674,7 @@
"'Si me lo permite, su respuesta es 1'"
]
},
- "execution_count": 16,
+ "execution_count": 14,
"metadata": {},
"output_type": "execute_result"
}
@@ -685,7 +685,7 @@
},
{
"cell_type": "code",
- "execution_count": 17,
+ "execution_count": 15,
"metadata": {
"slideshow": {
"slide_type": "subslide"
@@ -698,7 +698,7 @@
"'Si me lo permite, su respuesta es 100'"
]
},
- "execution_count": 17,
+ "execution_count": 15,
"metadata": {},
"output_type": "execute_result"
}
@@ -709,7 +709,7 @@
},
{
"cell_type": "code",
- "execution_count": 18,
+ "execution_count": 16,
"metadata": {
"slideshow": {
"slide_type": "subslide"
@@ -722,7 +722,7 @@
"['1', 100]"
]
},
- "execution_count": 18,
+ "execution_count": 16,
"metadata": {},
"output_type": "execute_result"
}
@@ -745,7 +745,7 @@
},
{
"cell_type": "code",
- "execution_count": 19,
+ "execution_count": 17,
"metadata": {
"slideshow": {
"slide_type": "subslide"
@@ -759,7 +759,7 @@
},
{
"cell_type": "code",
- "execution_count": 20,
+ "execution_count": 18,
"metadata": {
"slideshow": {
"slide_type": "subslide"
@@ -775,7 +775,7 @@
},
{
"cell_type": "code",
- "execution_count": 21,
+ "execution_count": 19,
"metadata": {
"slideshow": {
"slide_type": "subslide"
@@ -788,7 +788,7 @@
"2"
]
},
- "execution_count": 21,
+ "execution_count": 19,
"metadata": {},
"output_type": "execute_result"
}
@@ -834,7 +834,7 @@
},
{
"cell_type": "code",
- "execution_count": 23,
+ "execution_count": 20,
"metadata": {
"slideshow": {
"slide_type": "subslide"
@@ -847,7 +847,7 @@
"text": [
".s\n",
"----------------------------------------------------------------------\n",
- "Ran 2 tests in 0.073s\n",
+ "Ran 1 test in 0.001s\n",
"\n",
"OK (skipped=1)\n"
]
@@ -855,10 +855,10 @@
{
"data": {
"text/plain": [
- "<unittest.runner.TextTestResult run=2 errors=0 failures=0>"
+ "<unittest.runner.TextTestResult run=1 errors=0 failures=0>"
]
},
- "execution_count": 23,
+ "execution_count": 20,
"metadata": {},
"output_type": "execute_result"
}
@@ -899,22 +899,22 @@
]
},
{
- "cell_type": "code",
- "execution_count": 24,
+ "cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
- "outputs": [],
"source": [
+ "```python\n",
"import discard\n",
"\n",
"@discard.Statistics.register\n",
"class CountPosts:\n",
" \n",
" def __call__(self,posts):\n",
- " return len(posts)"
+ " return len(posts)\n",
+ "```"
]
},
{
@@ -929,20 +929,20 @@
]
},
{
- "cell_type": "code",
- "execution_count": 25,
+ "cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
- "outputs": [],
"source": [
+ "```python\n",
"import discard\n",
"\n",
"@discard.Validate.clear_emails\n",
"class Content(discard.Data):\n",
- " pass"
+ " pass\n",
+ "```"
]
},
{
@@ -958,7 +958,7 @@
},
{
"cell_type": "code",
- "execution_count": 26,
+ "execution_count": 21,
"metadata": {
"slideshow": {
"slide_type": "subslide"
@@ -977,7 +977,7 @@
},
{
"cell_type": "code",
- "execution_count": 27,
+ "execution_count": 22,
"metadata": {
"slideshow": {
"slide_type": "fragment"
@@ -990,7 +990,7 @@
"['Entero(1)', 'Flotante(0.99)', 'Entero(False)']"
]
},
- "execution_count": 27,
+ "execution_count": 22,
"metadata": {},
"output_type": "execute_result"
}
@@ -1001,7 +1001,7 @@
},
{
"cell_type": "code",
- "execution_count": 28,
+ "execution_count": 23,
"metadata": {
"slideshow": {
"slide_type": "subslide"
@@ -1030,7 +1030,7 @@
},
{
"cell_type": "code",
- "execution_count": 29,
+ "execution_count": 24,
"metadata": {
"slideshow": {
"slide_type": "subslide"
@@ -1043,7 +1043,7 @@
"['Entero(100)', 'Flotante(99.90)', 'Bool(1)']"
]
},
- "execution_count": 29,
+ "execution_count": 24,
"metadata": {},
"output_type": "execute_result"
}
@@ -1249,10 +1249,8 @@
]
},
{
- "cell_type": "code",
- "execution_count": null,
+ "cell_type": "markdown",
"metadata": {},
- "outputs": [],
"source": [
"Conozco un grupo de objetos que resuelven problemas\n",
"\n",
@@ -1303,7 +1301,7 @@
"metadata": {
"celltoolbar": "Slideshow",
"kernelspec": {
- "display_name": "Python 3",
+ "display_name": "Python 3 (ipykernel)",
"language": "python",
"name": "python3"
},
@@ -1317,7 +1315,7 @@
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
- "version": "3.8.6"
+ "version": "3.12.1"
}
},
"nbformat": 4,