README.md

Welcome to PyPOTS

a Python toolbox for machine learning on Partially-Observed Time Series

⦿ Motivation: Due to all kinds of reasons like failure of collection sensors, communication error, and unexpected malfunction, missing values are common to see in time series from the real-world environment. This makes partially-observed time series (POTS) a pervasive problem in open-world modeling and prevents advanced data analysis. Although this problem is important, the area of machine learning on POTS still lacks a dedicated toolkit. PyPOTS is created to fill in this blank.

⦿ Mission: PyPOTS (pronounced "Pie Pots") is born to become a handy toolbox that is going to make machine learning on POTS easy rather than tedious, to help engineers and researchers focus more on the core problems in their hands rather than on how to deal with the missing parts in their data. PyPOTS will keep integrating classical and the latest state-of-the-art machine learning algorithms for partially-observed multivariate time series. For sure, besides various algorithms, PyPOTS is going to have unified APIs together with detailed documentation and interactive examples across algorithms as tutorials.

🤗 Please star this repo to help others notice PyPOTS if you think it is a useful toolkit. Please properly cite PyPOTS in your publications if it helps with your research. This really means a lot to our open-source research. Thank you!

The rest of this readme file is organized as follows: ❖ Available Algorithms, ❖ PyPOTS Ecosystem, ❖ Installation, ❖ Usage, ❖ Citing PyPOTS, ❖ Contribution, ❖ Community.

❖ Available Algorithms

PyPOTS supports imputation, classification, clustering, forecasting, and anomaly detection tasks on multivariate partially-observed time series with missing values. The table below shows the availability of each algorithm (sorted by Year) in PyPOTS for different tasks. The symbol ✅ indicates the algorithm is available for the corresponding task (note that models will be continuously updated in the future to handle tasks that are not currently supported. Stay tuned❗️).

🌟 Since v0.2, all neural-network models in PyPOTS has got hyperparameter-optimization support. This functionality is implemented with the Microsoft NNI framework. You may want to refer to our time-series imputation survey repo Awesome_Imputation to see how to config and tune the hyperparameters.

🔥 Note that all models whose name with 🧑‍🔧 in the table (e.g. Transformer, iTransformer, Informer etc.) are not originally proposed as algorithms for POTS data in their papers, and they cannot directly accept time series with missing values as input, let alone imputation. To make them applicable to POTS data, we specifically apply the embedding strategy and training approach (ORT+MIT) the same as we did in the SAITS paper¹.

The task types are abbreviated as follows: IMPU: Imputation; FORE: Forecasting; CLAS: Classification; CLUS: Clustering; ANOD: Anomaly Detection. The paper references and links are all listed at the bottom of this file.

Type	Algo	IMPU	FORE	CLAS	CLUS	ANOD	Year - Venue
Neural Net	iTransformer🧑‍🔧2	✅					2024 - ICLR
Neural Net	SAITS1	✅					2023 - ESWA
Neural Net	FreTS🧑‍🔧3	✅					2023 - NeurIPS
Neural Net	Koopa🧑‍🔧4	✅					2023 - NeurIPS
Neural Net	Crossformer🧑‍🔧5	✅					2023 - ICLR
Neural Net	TimesNet6	✅					2023 - ICLR
Neural Net	PatchTST🧑‍🔧7	✅					2023 - ICLR
Neural Net	ETSformer🧑‍🔧8	✅					2023 - ICLR
Neural Net	MICN🧑‍🔧9	✅					2023 - ICLR
Neural Net	DLinear🧑‍🔧10	✅					2023 - AAAI
Neural Net	TiDE🧑‍🔧11	✅					2023 - TMLR
Neural Net	SCINet🧑‍🔧12	✅					2022 - NeurIPS
Neural Net	Nonstationary Tr.🧑‍🔧13	✅					2022 - NeurIPS
Neural Net	FiLM🧑‍🔧14	✅					2022 - NeurIPS
Neural Net	RevIN_SCINet🧑‍🔧15	✅					2022 - ICLR
Neural Net	Pyraformer🧑‍🔧16	✅					2022 - ICLR
Neural Net	Raindrop17			✅			2022 - ICLR
Neural Net	FEDformer🧑‍🔧18	✅					2022 - ICML
Neural Net	Autoformer🧑‍🔧19	✅					2021 - NeurIPS
Neural Net	CSDI20	✅	✅				2021 - NeurIPS
Neural Net	Informer🧑‍🔧21	✅					2021 - AAAI
Neural Net	US-GAN22	✅					2021 - AAAI
Neural Net	CRLI23				✅		2021 - AAAI
Probabilistic	BTTF24		✅				2021 - TPAMI
Neural Net	StemGNN🧑‍🔧25	✅					2020 - NeurIPS
Neural Net	Reformer🧑‍🔧26	✅					2020 - ICLR
Neural Net	GP-VAE27	✅					2020 - AISTATS
Neural Net	VaDER28				✅		2019 - GigaSci.
Neural Net	M-RNN29	✅					2019 - TBME
Neural Net	BRITS30	✅		✅			2018 - NeurIPS
Neural Net	GRU-D31	✅		✅			2018 - Sci. Rep.
Neural Net	Transformer🧑‍🔧32	✅					2017 - NeurIPS
Naive	LOCF/NOCB	✅
Naive	Mean	✅
Naive	Median	✅

❖ PyPOTS Ecosystem

At PyPOTS, things are related to coffee, which we're familiar with. Yes, this is a coffee universe! As you can see, there is a coffee pot in the PyPOTS logo. And what else? Please read on ;-)

👈 Time series datasets are taken as coffee beans at PyPOTS, and POTS datasets are incomplete coffee beans with missing parts that have their own meanings. To make various public time-series datasets readily available to users, Time Series Data Beans (TSDB) is created to make loading time-series datasets super easy! Visit TSDB right now to know more about this handy tool 🛠, and it now supports a total of 169 open-source datasets!

👉 To simulate the real-world data beans with missingness, the ecosystem library PyGrinder, a toolkit helping grind your coffee beans into incomplete ones, is created. Missing patterns fall into three categories according to Robin's theory³³: MCAR (missing completely at random), MAR (missing at random), and MNAR (missing not at random). PyGrinder supports all of them and additional functionalities related to missingness. With PyGrinder, you can introduce synthetic missing values into your datasets with a single line of code.

👈 Now we have the beans, the grinder, and the pot, how to brew us a cup of coffee? Tutorials are necessary! Considering the future workload, PyPOTS tutorials are released in a single repo, and you can find them in BrewPOTS. Take a look at it now, and learn how to brew your POTS datasets!

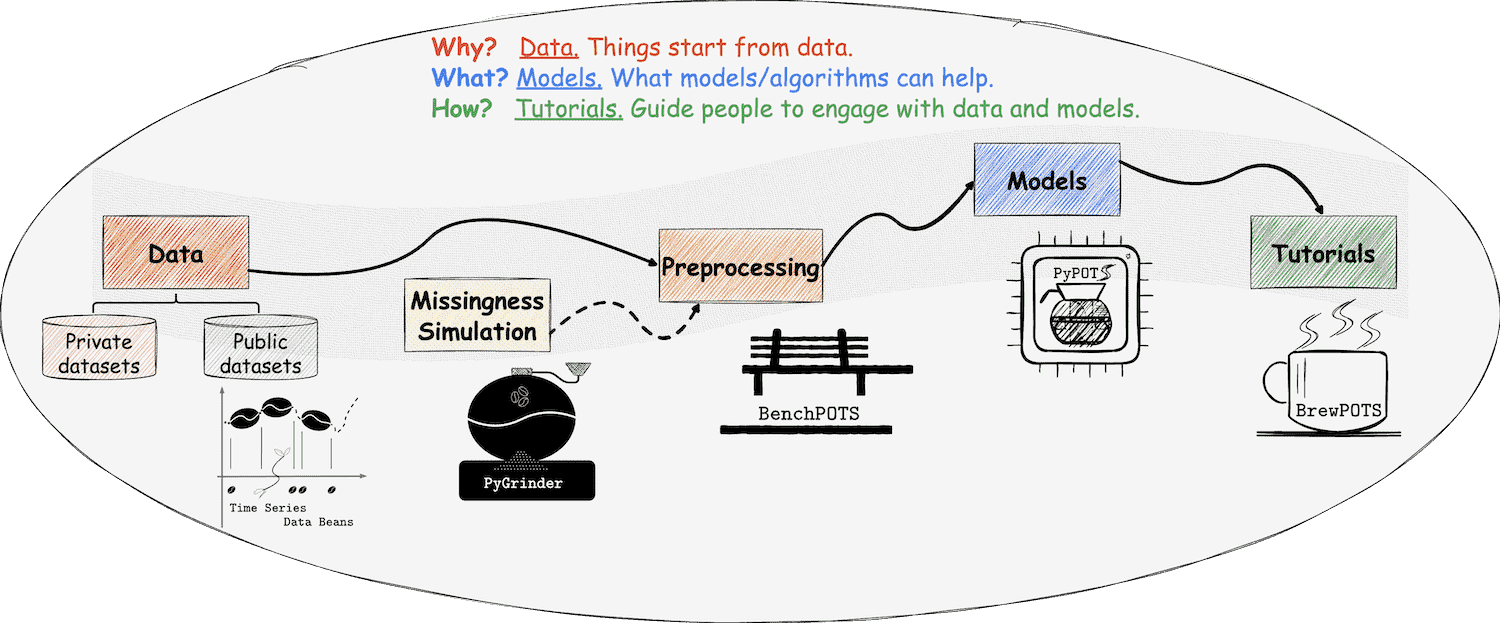
☕️ Welcome to the universe of PyPOTS. Enjoy it and have fun!

❖ Installation

You can refer to the installation instruction in PyPOTS documentation for a guideline with more details.

PyPOTS is available on both PyPI and Anaconda. You can install PyPOTS like below as well as TSDB and PyGrinder:

# via pip
pip install pypots            # the first time installation
pip install pypots --upgrade  # update pypots to the latest version
# install from the latest source code with the latest features but may be not officially released yet
pip install https://github.com/WenjieDu/PyPOTS/archive/main.zip

# via conda
conda install -c conda-forge pypots  # the first time installation
conda update  -c conda-forge pypots  # update pypots to the latest version

❖ Usage

Besides BrewPOTS, you can also find a simple and quick-start tutorial notebook on Google Colab . If you have further questions, please refer to PyPOTS documentation docs.pypots.com. You can also raise an issue or ask in our community.

We present you a usage example of imputing missing values in time series with PyPOTS below, you can click it to view.

Click here to see an example applying SAITS on PhysioNet2012 for imputation:

# Data preprocessing. Tedious, but PyPOTS can help.
import numpy as np
from sklearn.preprocessing import StandardScaler
from pygrinder import mcar
from pypots.data import load_specific_dataset
data = load_specific_dataset('physionet_2012')  # PyPOTS will automatically download and extract it.
X = data['X']
num_samples = len(X['RecordID'].unique())
X = X.drop(['RecordID', 'Time'], axis = 1)
X = StandardScaler().fit_transform(X.to_numpy())
X = X.reshape(num_samples, 48, -1)
X_ori = X  # keep X_ori for validation
X = mcar(X, 0.1)  # randomly hold out 10% observed values as ground truth
dataset = {"X": X}  # X for model input
print(X.shape)  # (11988, 48, 37), 11988 samples and each sample has 48 time steps, 37 features

# Model training. This is PyPOTS showtime.
from pypots.imputation import SAITS
from pypots.utils.metrics import calc_mae
saits = SAITS(n_steps=48, n_features=37, n_layers=2, d_model=256, n_heads=4, d_k=64, d_v=64, d_ffn=128, dropout=0.1, epochs=10)
# Here I use the whole dataset as the training set because ground truth is not visible to the model, you can also split it into train/val/test sets
saits.fit(dataset)  # train the model on the dataset
imputation = saits.impute(dataset)  # impute the originally-missing values and artificially-missing values
indicating_mask = np.isnan(X) ^ np.isnan(X_ori)  # indicating mask for imputation error calculation
mae = calc_mae(imputation, np.nan_to_num(X_ori), indicating_mask)  # calculate mean absolute error on the ground truth (artificially-missing values)
saits.save("save_it_here/saits_physionet2012.pypots")  # save the model for future use
saits.load("save_it_here/saits_physionet2012.pypots")  # reload the serialized model file for following imputation or training

❖ Citing PyPOTS

Tip

[Updates in Feb 2024] 😎 Our survey paper Deep Learning for Multivariate Time Series Imputation: A Survey has been released on arXiv. The code is open source in the GitHub repo Awesome_Imputation. We comprehensively review the literature of the state-of-the-art deep-learning imputation methods for time series, provide a taxonomy for them, and discuss the challenges and future directions in this field.

[Updates in Jun 2023] 🎉 A short version of the PyPOTS paper is accepted by the 9th SIGKDD international workshop on Mining and Learning from Time Series (MiLeTS'23)). Additionally, PyPOTS has been included as a PyTorch Ecosystem project.

The paper introducing PyPOTS is available on arXiv at this URL, and we are pursuing to publish it in prestigious academic venues, e.g. JMLR (track for Machine Learning Open Source Software). If you use PyPOTS in your work, please cite it as below and 🌟star this repository to make others notice this library. 🤗

There are scientific research projects using PyPOTS and referencing in their papers. Here is an incomplete list of them.

@article{du2023pypots,
title={{PyPOTS: a Python toolbox for data mining on Partially-Observed Time Series}},
author={Wenjie Du},
year={2023},
eprint={2305.18811},
archivePrefix={arXiv},
primaryClass={cs.LG},
url={https://arxiv.org/abs/2305.18811},
doi={10.48550/arXiv.2305.18811},
}

or

Wenjie Du. (2023). PyPOTS: a Python toolbox for data mining on Partially-Observed Time Series. arXiv, abs/2305.18811.https://arxiv.org/abs/2305.18811

❖ Contribution

You're very welcome to contribute to this exciting project!

By committing your code, you'll

1. make your well-established model out-of-the-box for PyPOTS users to run, and help your work obtain more exposure and impact. Take a look at our inclusion criteria. You can utilize the template folder in each task package (e.g. pypots/imputation/template) to quickly start;
2. become one of PyPOTS contributors and be listed as a volunteer developer on the PyPOTS website;
3. get mentioned in our release notes;

You can also contribute to PyPOTS by simply staring🌟 this repo to help more people notice it. Your star is your recognition to PyPOTS, and it matters!

👏 Click here to view PyPOTS stargazers and forkers.
We're so proud to have more and more awesome users, as well as more bright ✨stars:

👀 Check out a full list of our users' affiliations on PyPOTS website here!

❖ Community

We care about the feedback from our users, so we're building PyPOTS community on

• Slack. General discussion, Q&A, and our development team are here;
• LinkedIn. Official announcements and news are here;
• WeChat (微信公众号). We also run a group chat on WeChat, and you can get the QR code from the official account after following it;

If you have any suggestions or want to contribute ideas or share time-series related papers, join us and tell. PyPOTS community is open, transparent, and surely friendly. Let's work together to build and improve PyPOTS!

🏠 Visits

Footnotes

1. Du, W., Cote, D., & Liu, Y. (2023). SAITS: Self-Attention-based Imputation for Time Series. Expert systems with applications. ↩ ↩²

2. Liu, Y., Hu, T., Zhang, H., Wu, H., Wang, S., Ma, L., & Long, M. (2024). iTransformer: Inverted Transformers Are Effective for Time Series Forecasting. ICLR 2024. ↩

3. Yi, K., Zhang, Q., Fan, W., Wang, S., Wang, P., He, H., An, N., Lian, D., Cao, L., & Niu, Z. (2023). Frequency-domain MLPs are More Effective Learners in Time Series Forecasting. NeurIPS 2023. ↩

4. Liu, Y., Li, C., Wang, J., & Long, M. (2023). Koopa: Learning Non-stationary Time Series Dynamics with Koopman Predictors. NeurIPS 2023. ↩

5. Zhang, Y., & Yan, J. (2023). Crossformer: Transformer utilizing cross-dimension dependency for multivariate time series forecasting. ICLR 2023. ↩

6. Wu, H., Hu, T., Liu, Y., Zhou, H., Wang, J., & Long, M. (2023). TimesNet: Temporal 2d-variation modeling for general time series analysis. ICLR 2023 ↩

7. Nie, Y., Nguyen, N. H., Sinthong, P., & Kalagnanam, J. (2023). A time series is worth 64 words: Long-term forecasting with transformers. ICLR 2023 ↩

8. Woo, G., Liu, C., Sahoo, D., Kumar, A., & Hoi, S. (2023). ETSformer: Exponential Smoothing Transformers for Time-series Forecasting. ICLR 2023 ↩

9. Wang, H., Peng, J., Huang, F., Wang, J., Chen, J., & Xiao, Y. (2023). MICN: Multi-scale Local and Global Context Modeling for Long-term Series Forecasting. ICLR 2023. ↩

10. Zeng, A., Chen, M., Zhang, L., & Xu, Q. (2023). Are transformers effective for time series forecasting?. AAAI 2023 ↩

11. Das, A., Kong, W., Leach, A., Mathur, S., Sen, R., & Yu, R. (2023). Long-term Forecasting with TiDE: Time-series Dense Encoder. TMLR 2023. ↩

12. Liu, M., Zeng, A., Chen, M., Xu, Z., Lai, Q., Ma, L., & Xu, Q. (2022). SCINet: Time Series Modeling and Forecasting with Sample Convolution and Interaction. NeurIPS 2022. ↩

13. Liu, Y., Wu, H., Wang, J., & Long, M. (2022). Non-stationary Transformers: Exploring the Stationarity in Time Series Forecasting. NeurIPS 2022. ↩

14. Zhou, T., Ma, Z., Wen, Q., Sun, L., Yao, T., Yin, W., & Jin, R. (2022). FiLM: Frequency improved Legendre Memory Model for Long-term Time Series Forecasting. NeurIPS 2022. ↩

15. Kim, T., Kim, J., Tae, Y., Park, C., Choi, J. H., & Choo, J. (2022). Reversible Instance Normalization for Accurate Time-Series Forecasting against Distribution Shift. ICLR 2022. ↩

16. Liu, S., Yu, H., Liao, C., Li, J., Lin, W., Liu, A. X., & Dustdar, S. (2022). Pyraformer: Low-Complexity Pyramidal Attention for Long-Range Time Series Modeling and Forecasting. ICLR 2022. ↩

17. Zhang, X., Zeman, M., Tsiligkaridis, T., & Zitnik, M. (2022). Graph-Guided Network for Irregularly Sampled Multivariate Time Series. ICLR 2022. ↩

18. Zhou, T., Ma, Z., Wen, Q., Wang, X., Sun, L., & Jin, R. (2022). FEDformer: Frequency enhanced decomposed transformer for long-term series forecasting. ICML 2022. ↩

19. Wu, H., Xu, J., Wang, J., & Long, M. (2021). Autoformer: Decomposition transformers with auto-correlation for long-term series forecasting. NeurIPS 2021. ↩

20. Tashiro, Y., Song, J., Song, Y., & Ermon, S. (2021). CSDI: Conditional Score-based Diffusion Models for Probabilistic Time Series Imputation. NeurIPS 2021. ↩

21. Zhou, H., Zhang, S., Peng, J., Zhang, S., Li, J., Xiong, H., & Zhang, W. (2021). Informer: Beyond efficient transformer for long sequence time-series forecasting. AAAI 2021. ↩

22. Miao, X., Wu, Y., Wang, J., Gao, Y., Mao, X., & Yin, J. (2021). Generative Semi-supervised Learning for Multivariate Time Series Imputation. AAAI 2021. ↩

23. Ma, Q., Chen, C., Li, S., & Cottrell, G. W. (2021). Learning Representations for Incomplete Time Series Clustering. AAAI 2021. ↩

24. Chen, X., & Sun, L. (2021). Bayesian Temporal Factorization for Multidimensional Time Series Prediction. IEEE transactions on pattern analysis and machine intelligence. ↩

25. Cao, D., Wang, Y., Duan, J., Zhang, C., Zhu, X., Huang, C., Tong, Y., Xu, B., Bai, J., Tong, J., & Zhang, Q. (2020). Spectral Temporal Graph Neural Network for Multivariate Time-series Forecasting. NeurIPS 2020. ↩

26. Kitaev, N., Kaiser, Ł., & Levskaya, A. (2020). Reformer: The Efficient Transformer. ICLR 2020. ↩

27. Fortuin, V., Baranchuk, D., Raetsch, G. & Mandt, S. (2020). GP-VAE: Deep Probabilistic Time Series Imputation. AISTATS 2020. ↩

28. Jong, J.D., Emon, M.A., Wu, P., Karki, R., Sood, M., Godard, P., Ahmad, A., Vrooman, H.A., Hofmann-Apitius, M., & Fröhlich, H. (2019). Deep learning for clustering of multivariate clinical patient trajectories with missing values. GigaScience. ↩

29. Yoon, J., Zame, W. R., & van der Schaar, M. (2019). Estimating Missing Data in Temporal Data Streams Using Multi-Directional Recurrent Neural Networks. IEEE Transactions on Biomedical Engineering. ↩

30. Cao, W., Wang, D., Li, J., Zhou, H., Li, L., & Li, Y. (2018). BRITS: Bidirectional Recurrent Imputation for Time Series. NeurIPS 2018. ↩

31. Che, Z., Purushotham, S., Cho, K., Sontag, D.A., & Liu, Y. (2018). Recurrent Neural Networks for Multivariate Time Series with Missing Values. Scientific Reports. ↩

32. Vaswani, A., Shazeer, N.M., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A.N., Kaiser, L., & Polosukhin, I. (2017). Attention is All you Need. NeurIPS 2017. ↩

33. Rubin, D. B. (1976). Inference and missing data. Biometrika. ↩