45_LDA算法原理.md

问题

线性判别分析（Linear Discriminant Analysis，LDA）是机器学习中常用的降维方法之一，本文旨在介绍LDA算法的思想，其数学推导过程可能会稍作简化。

LDA的思想

● LDA是一种线性的、有监督的降维方法，即每个样本都有对应的类别标签（这点和PCA）。

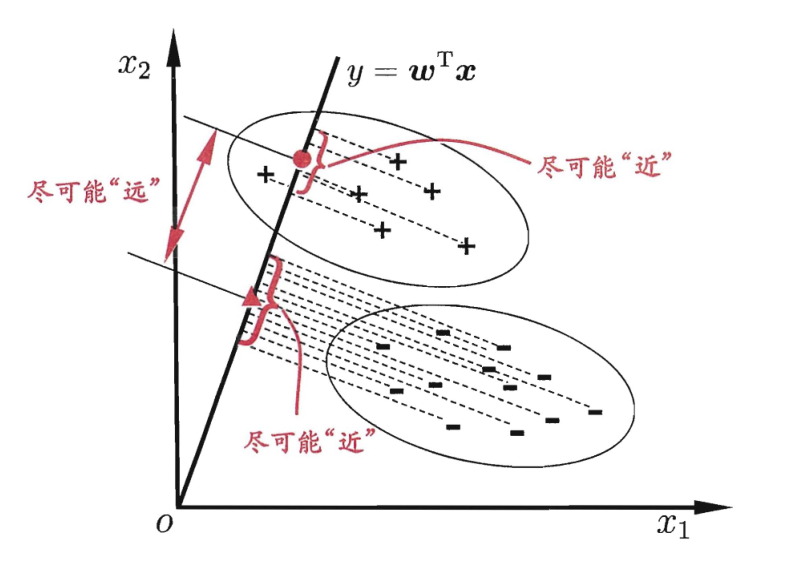
● 主要思想：给定训练样本集，设法将样本投影到一条直线上，使得同类的样本的投影尽可能的接近、异类样本的投影尽可能地远离（即最小化类内距离和最大化类间距离）。

下面分别通过《机器学习》和《百面机器学习》两本书中的图片先来直观地理解一下LDA的思想。

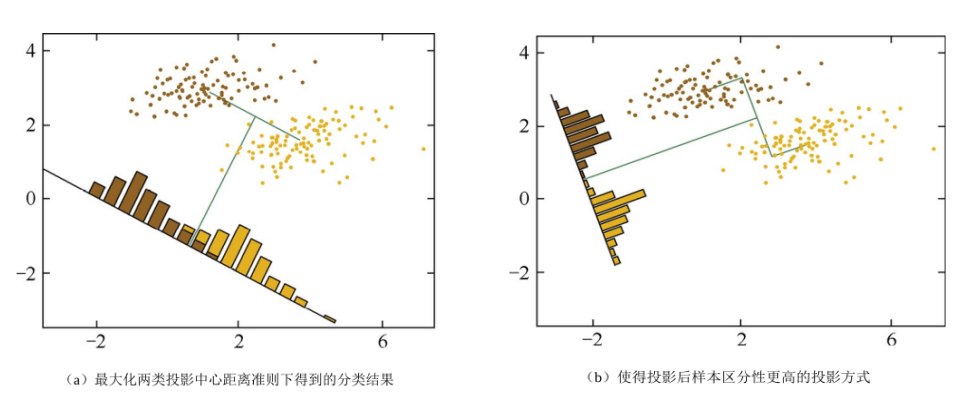
● 为什么要将最大化类间距离和最小化类内距离同时作为优化目标呢？

先看上面第二张图的左图（a），对于两个类别，只采用了最大化类间距离，其结果中两类样本会有少许重叠；而对于右图（b），同时最大化类间距离和最小化类内距离，可见分类效果更好，同类样本的投影分布更加集中了。当然，对于二维的数据，可以采用将样本投影到直线上的方式，对于高维的数据，则是投影到一个低维的超平面上，这应该很好理解。

LDA算法优化目标

由上面的介绍我们知道，LDA算法的思想就是最大化类间距离和最小化类内距离，其优化目标就很直观了，那怎么用数学方式来表示呢？要解决这个问题，就得先看看怎么描述类间距离和类内距离。

● 类间距离（以二分类为示例）

假设有$C_{1}$、$C_{2}$两类样本，其均值分别为 $\mu_{1}=\frac{1}{N}\sum_{x\in C_{1}}x$ 和 $\mu_{2}=\frac{1}{N}\sum_{x\in C_{2}}x$ 。很显然，要使得两类样本类间距离最大，则 $\mu_{1}$ 、$\mu_{2}$ 的距离应尽可能地大，则类间距离可描述为 $$ ||\omega^{T}\mu_{0}-\omega^{T}\mu_{1}||_{2}^{2},\ \ 其中，\omega为投影方向 $$ ● 类内距离

要使得样本在同类中距离最小，也就是最小化同类样本的方差，假设分别用 $D_{1}$、 $D_{2}$ 表示两类样本的投影方差，则有： $$ D_{1} = \sum_{x\in C_{1}}(\omega^{T}x-\omega^{T}\mu_{1})^{2}=\sum_{x\in C_{1}}\omega^{T}(x-\mu_{1})(x-\mu_{1})^{T}\omega \ D_{2} = \sum_{x\in C_{2}}(\omega^{T}x-\omega^{T}\mu_{2})^{2}=\sum_{x\in C_{2}}\omega^{T}(x-\mu_{2})(x-\mu_{2})^{T}\omega $$ 因此，要使得类内距离最小，就是要最小化 $D_{1}+D_{2}$。

● 优化目标

由上面分析，最大化类间距离和最小化类内距离，因此可以得到最大化目标： $$ J(\omega) = \frac{||\omega^{T}\mu_{0}-\omega^{T}\mu_{1}||{2}^{2}}{D{1}+D_{2}}\\qquad\qquad\qquad\quad =\frac{||\omega^{T}\mu_{0}-\omega^{T}\mu_{1}||{2}^{2}}{\sum{x\in C_{i}}\omega^{T}(x-\mu_{i})(x-\mu_{i})^{T}\omega} $$ 为了化简上面公式，给出几个定义：

● 类间散度矩阵： $$ S_{b}=(\mu_{1}-\mu_{2})(\mu_{1}-\mu_{2})^{T} $$ ● 类内散度矩阵： $$ S_{\omega}=\Sigma_{1}+\Sigma_{2}=\sum_{x\in C_{1}}(x-\mu_{1})(x-\mu_{1})^{T}+\sum_{x\in C_{2}}(x-\mu_{2})(x-\mu_{2})^{T} $$ 因此最大化目标可以简写为： $$ J(\omega) = \frac{\omega^{T}S_{b}\omega}{\omega^{T}S_{\omega}\omega} $$

这是一个广义瑞利商，可以对矩阵进行标准化操作（具体证明就不展开啦），因此，通过标准化后总可以得到 $\omega^{T}S_{\omega}\omega=1$，又由于上面优化目标函数分子分母都是二次项，其解与 $\omega$ 的长度无关，只与方向有关，因此上面优化目标等价于以下最小化目标：

转化为最小化目标： $$ \underset{\omega}{min}\quad-\omega^{T}S_{b}\omega \ s.t. \quad \omega^{T}S_{\omega}\omega=1 $$ 由拉格朗日法，上式可得： $$ S_{b}\omega=\lambda S_{\omega}\omega \ 即有，S_{\omega}^{-1}S_{b}\omega=\lambda \omega $$ 至此，我们的优化目标就转化成了求矩阵 $S_{\omega}^{-1}S_{b}$ 的特征值，而投影方向就是这个特征值对应的特征向量。

由于 $(\mu_{1}-\mu_{2})^{T}\omega$ 是个标量（因为 $\mu_{1}-\mu_{2}$ 和 $\omega$ 同向时才能保证类间距离最大），

所以，对于 $S_{b}\omega=(\mu_{1}-\mu_{2})(\mu_{1}-\mu_{2})^{T}\omega$ 而言，可以看出 $S_{b}\omega$ 始终与 $(\mu_{1}-\mu_{2})$ 的方向一致

因此，如果只考虑 $\omega$ 的长度而不考虑方向，则由： $$ S_{\omega}^{-1}S_{b}\omega=\lambda \omega \qquad => \qquad \omega=S_{\omega}^{-1}(\mu_{1}-\mu_{2}) $$ 也就是说，我们只需求出样本的均值和类内的散度矩阵（即类内方差），即可求出投影方向。

LDA算法流程(推广至高维)

1.计算每类样本的均值向量 $\mu_{i}$。

2.计算类间散度矩阵 $S_{\omega}$ 和类内散度矩阵 $S_{b}$ 。

3.求矩阵 $S_{\omega}^{-1}S_{b}$ 的特征值即对应的特征向量，从大到小排序。

4.将特征值由大到小排列，取出前 k 个特征值对应的特征向量。

5.将 n 维样本映射到 k 维，实现降维处理。 $$ x_{i}^{'}=\begin{bmatrix}\omega_{1}^{T}x_{i}\\omega_{2}^{T}x_{i}\\vdots \\omega_{k}^{T}x_{i} \end{bmatrix}\ $$

总结

● LDA是线性的、有监督的降维方法，其优点是善于对有类别信息的数据进行降维处理（与PCA的不同）。

● LDA因为是线性模型，对噪声的鲁棒性较好，但由于模型简单，对数据特征的表达能力不足。

● LDA对数据的分布做了一些很强的假设，比如每个类别都是高斯分布、各个类别的协方差相等，实际中这些假设很难完全满足。

关于LDA与PCA的区别，请看下回分解。

参考资料

周志华《机器学习》

葫芦娃《百面机器学习》