01.01.24

Author: Devinterview-io

README.md

@@ -574,31 +574,30 @@ class HashTable:
 
 1. **Linear Probing**: When a collision occurs, investigate cells in a consistent sequence. The operation is mathematically represented as:
 
-   $$
-   (h(k) + i) \mod m, \quad  \text{for} \ i = 0, 1, 2, \ldots
-   $$
+$$
+(h(k) + i) \mod m, \quad  \text{for} \ i = 0, 1, 2, \ldots
+$$
 
-   Here, $h(k)$ is the key's hash value, $m$ is the table size, and $i$ iterates within the modulo operation.
+Here, $h(k)$ is the key's hash value, $m$ is the table size, and $i$ iterates within the modulo operation.
 
-   ![Linear Probing](https://upload.wikimedia.org/wikipedia/commons/b/bf/Linear_ probing_visualisation.svg)
 
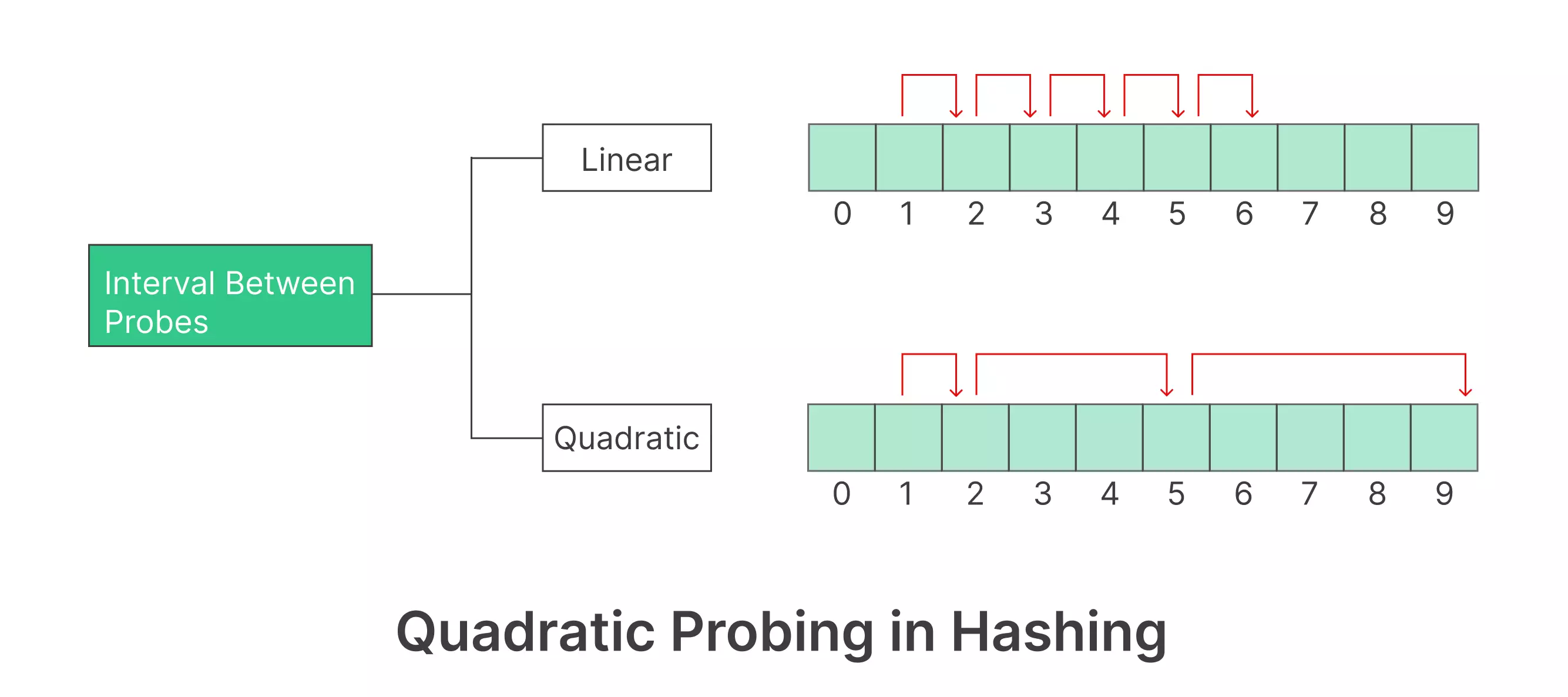
 2. **Quadratic Probing**: The cells to search are determined by a quadratic function:
 
-   $$
-   (h(k) + c_1i + c_2i^2) \mod m
-   $$
+$$
+(h(k) + c_1i + c_2i^2) \mod m
+$$
 
-   Positive constants $c1$ and $c2$ are used as increment factors. If the table size is a prime number, these constants can equal 1 and 1, respectively. This scheme can still result in clustering.
+Positive constants $c1$ and $c2$ are used as increment factors. If the table size is a prime number, these constants can equal 1 and 1, respectively. This scheme can still result in clustering.
 
-   ![Quadratic Probing](https://upload.wikimedia.org/wikipedia/commons/9/98/Quadratic_probing_visualisation.svg)
+![Linear and Quadratic probing in hashing](https://firebasestorage.googleapis.com/v0/b/dev-stack-app.appspot.com/o/hash-tables%2Flinear-and-quadratic-probing-in-hashing.webp?alt=media&token=2aca1d94-be59-4c05-aa4d-2b3d50899053)
 
-3. **Double Hashing**: Unlike with linear or quadratic probing, the second hash function $h_2(k)$ computes the stride of the probe. The operation is:
+4. **Double Hashing**: Unlike with linear or quadratic probing, the second hash function $h_2(k)$ computes the stride of the probe. The operation is:
 
-   $$
-   (h(k) + ih_2(k)) \mod m
-   $$
+$$
+(h(k) + ih_2(k)) \mod m
+$$
 
-   **Note**: It's crucial for the new probe sequence to cover all positions in the table, thereby ensuring that every slot has the same probability of being the data's final location.
+**Note**: It's crucial for the new probe sequence to cover all positions in the table, thereby ensuring that every slot has the same probability of being the data's final location.
 <br>
 
 ## 11. Explain the _Time_ and _Space Complexity_ of a _Hash Table_.